Расчёт и конструирование механических передач

Рассмотрим двухступенчатую механическую передачу. Первую ступень этой передачи составляет косозубая цилиндрическая передача, а вторую – коническая. Кинематическая схема передачи показана на рис. 9.1, а исходные данные для расчёта указаны в табл. 9.5.

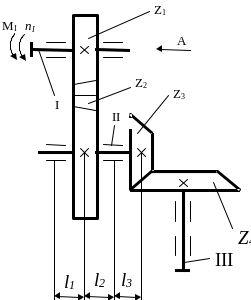
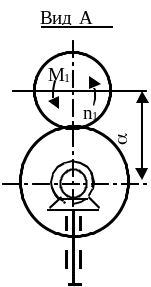
Рис. 9.1 Кинематическая схема

Таблица 9.5

Исходные данные

m1	m3 (mе)	1	3	nI					l1	l2	l3	MI
мм		. . .			Z1	Z2	Z3	Z4	м			Н·м
1,5	2,0	10	0	950	30	90	40	60	0,1	0,1	0,1	10

Геометрический расчёт зубчатых передач

Определяем основные размеры шестерни и колеса цилиндрической косозубой передачи (табл. 9.1) [16, 18].

Диаметры делительных окружностей:

Диаметры вершин зубьев:

Диаметры впадин:

Межосевое расстояние

Ширина зубчатых колёс

Определяем основные размеры шестерни и колеса конической прямозубой передачи (табл. 9.2) [16, 18]

Внешние делительные диаметры:

Углы делительных конусов:

Внешние диаметры вершин зубьев:

Внешние диаметры впадин:

Внешнее конусное расстояние

Ширина зубчатого венца колёс

Принимаем b = 21 мм.

Результаты расчётов сводим в табл. 9.6.

Таблица 9.6

Тип	Обозначение	Значения параметров, мм
передачи	параметров	шестерня	колесо
Цилиндрическая косозубая	d	45,69	137,06
	da	48,69	140,06
	df	41,94	133,31
	b	30	27
	a	91,38
Коническая прямозубая	de	80	120
		33,69	56,31
	dae	83,33	122,22
	dfe	76,01	117,34
	Rе	72,12
	b	21

Силы, действующие в зацеплениях

Определяем силы, действующие в зацеплении цилиндрической косозубой передачи (табл. 9.4) (рис. 9.2) [16, 18] с учетом направления сил.

Рис. 9.2. Силы, действующие в зацеплениях

Окружная сила

Осевая сила

Радиальная сила

Определяем силы, действующие в зацеплении конической прямозубой передачи ( табл. 9.4) [16, 18]

Окружная сила

где

Радиальная сила

Осевая сила

Результаты расчётов сводим в табл. 9.7.

Таблица 9.7

Тип передачи	Обозначение силы	Значение силы, Н
Цилиндрическая косозубая	Ft1 = Ft2	438
	Fz1 = Fz2	77
	Fr1 = Fr2	162
Коническая прямозубая	Ft3 = Ft4	875
	Fz3 = Fr4	177
	Fr3 = Fz4	265

Приближённый расчёт вала II на прочность

Расчётная схема вала II показана на рис. 9.3. При составлении расчётной схемы вала силы, действующие в зацеплениях, приведены к центру тяжести сечений B и D [22].

При этом изгибающие моменты

а крутящий момент

Построение графика изгибающего момента М_х

Вычисляем реакции опор в плоскости YOZ.

Используя уравнения равновесия

получим

Стержень имеет три участка АВ, ВС и CD (рис. 9.3). Используя метод сечений, составляем уравнения изгибающего момента М_х и вычисляем его значения на границах участков [22].

Участок АВ, 0  z₁  l_{1 .}

Участок ВС, l₁  z₂  (l₁+l₂).

Участок СD, 0  z₃  l₃ .

По результатам расчётов строим график М_Х (рис. 9.3).

Построение графика изгибающего момента М_У

Вычисляем реакции опор в плоскости XOZ.