Для закрепления знаний по вычислению всф в прил.2 приведены варианты индивидуальных заданий. Примеры решения задач
Задача 1
Построить эпюры ВСФ для стержня (рис. 2.8)
Находим
реакцию опоры
из уравнения статики
.
Составляем уравнение N на каждом из двух участков.
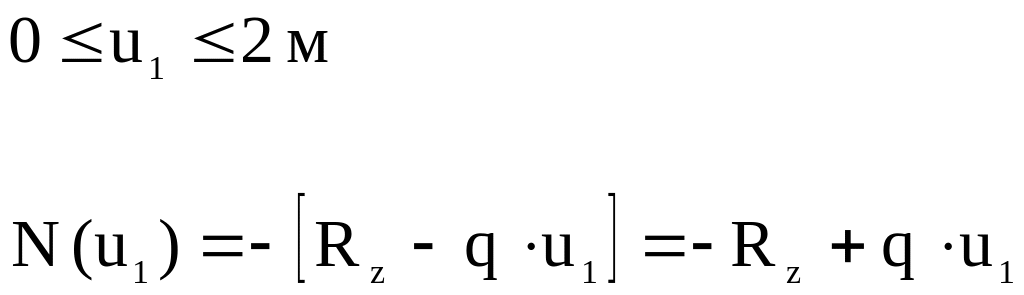
Находим значение N по границам участка
;
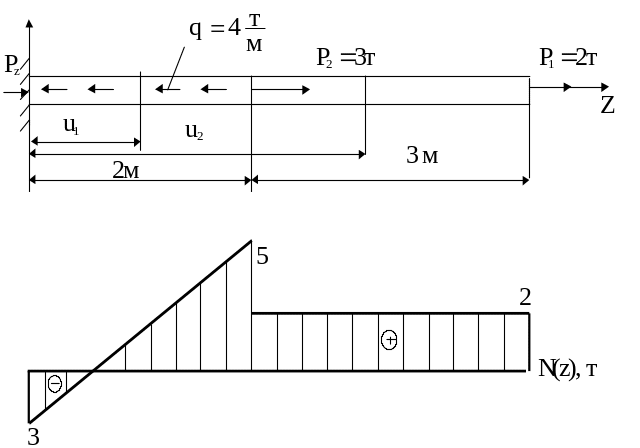Рис.
2.8
Нетрудно заметить, что
.
Остальные ВСФ для всех сечений стержня равны нулю. Эпюра продольных сил показана на рис. 2.8
В сечениях, где приложены осевые сосредоточенные силы, на эпюре продольных сил имеется разрыв на величину этих сил. В остальных сечениях разрывов на эпюре продольных сил нет.
Задача 2
Для заданной схемы нагружения стержня (рис. 2.9) построить эпюру (график)
продольных сил, если P=1,25 ql.
1. Так как левое концевое сечение стержня защемлено, то в заделке возникает реакция R. Эту реакцию определяем из условия равновесия всего стержня. Предположим, что направление реакции R совпадает с положительным направлением оси Z, тогда
,
.
Реакция R получилась положительной, следовательно, ее направление выбрано верно.
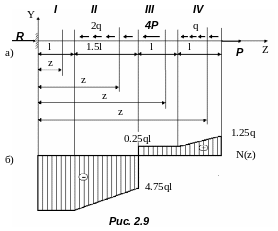
2. Разбиваем стержень на участки, в пределах которых функция N(z) непрерывна. Границами таких участков являются сечения, которые совпадают с местами приложения сосредоточенных сил, начала и конца действия распределенной нагрузки и концами стержня.
3. Рассмотрим часть стержня, ограниченную началом координат и произвольной абсциссой z на рассматриваемом участке.
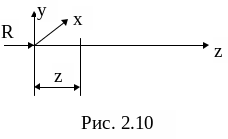
и
, т.е.
.
Продольная сила в этом сечении по
определению будет равна взятой со знаком
минус сумме проекций всех внешних сил,
приложенных на левую часть стержня
длиной z
на ось z:
.
На всем участке внутренняя сила постоянна,
а знак минус указывает, что она является
сжимающей.
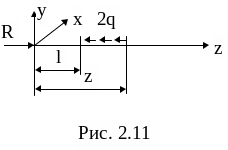
Второй
участок (рис 2.11). Границами II
участка являются сечения
и
,
.
На втором участке продольная сила
изменяется по линейному закону, поэтому
достаточно вычислить ее значения в
начале и конце второго участка:
,
.
Третий участок (рис.2.12)
,
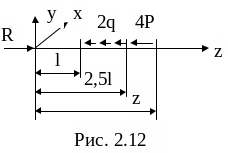
На
этом участке продольная сила постоянная
и растягивающая. Следует отметить, что
в сечении
имеет место
разрыв функции N(z)
на величину 4P.
Четвертый участок (рис. 2.13)
,
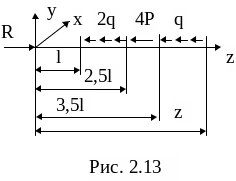
На четвертом участке продольная сила опять изменяется по линейному закону:
,
.
4. Построение эпюры N(z) (рис. 2.9). Ось эпюры проводят параллельно оси стержня. Вверх от оси откладывают положительные значения продольной силы, а вниз-отрицательные. Участок стержня, где продольная сила положительна, растянут, а где отрицательна – сжат.
Уравнение продольных сил в произвольном сечении с абсциссой z удобно записывать в одну строку, ограничив участки вертикальными линиями. Например, для рассмотренной задачи уравнение N(z) записывается в следующем виде:
.
Задача 3
Построить
эпюры ВСФ для стержня (рис. 2.14) , нагруженного
двумя сосредоточенными моментами и
погонной моментной нагрузкой постоянной
интенсивности.
Рис.2.14
Последняя не задана, но ее можно найти из уравнения равновесия всего стержня: сумма моментов всех внешних нагрузок относительно оси стержня равна нулю.
откуда
Уравнения ВСФ:
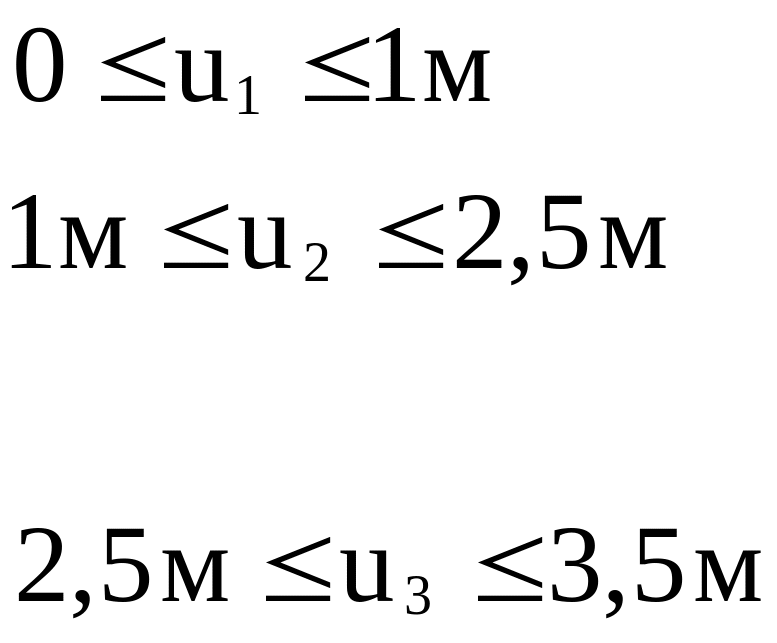
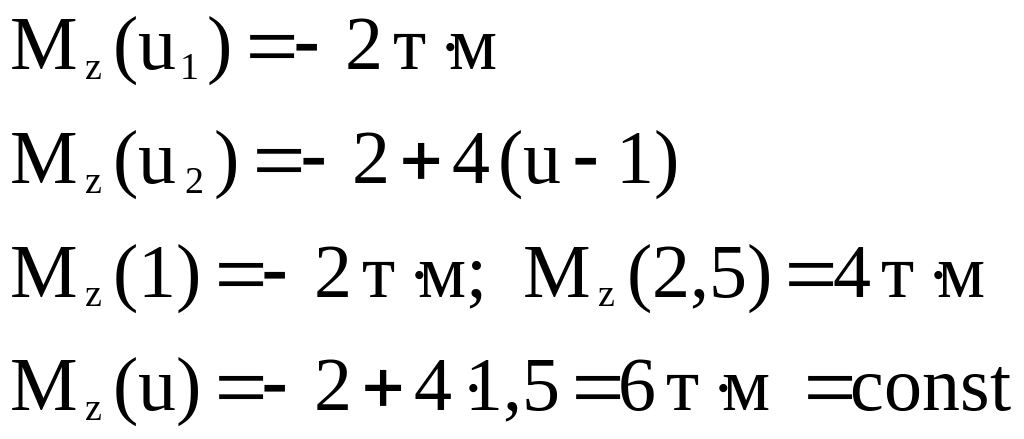
Остальные ВСФ во всех сечениях стержня равны нулю. Эпюра крутящих моментов показана на рис. 2.14.
На
первом и третьем участках угол наклона
касательной к эпюре крутящих моментов
равен нулю, так как интенсивность
погонной моментной нагрузки равна нулю.
На среднем участке угол наклона
касательной к эпюре крутящих моментов
постоянен и равен интенсивности погонной
нагрузки
.
В концевых сечениях, в которых приложены внешние сосредоточенные моменты, на эпюре крутящих моментов имеются разрывы на величину этих моментов. В остальных сечениях разрывов нет.
Задача 4
Для приведенной схемы нагружения вала (рис. 2.15 а) построить эпюру крутящих моментов, если L=0,5ml.
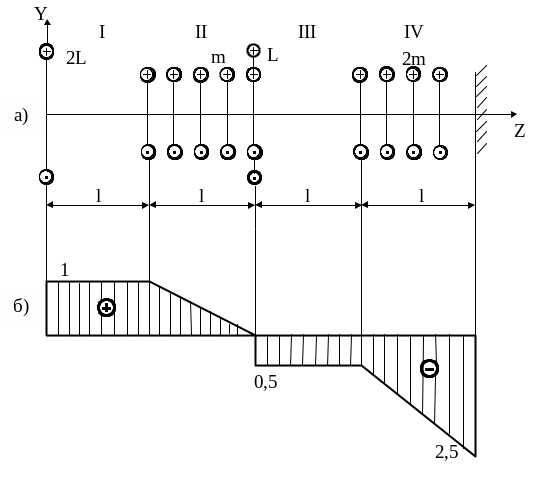
Рис. 2.15
Разбиваем вал на четыре участка, в пределах которых функция непрерывна. Запишем уравнение для определения крутящих моментов в произвольном сечении с абсциссой z , ограничив участки вертикальными линиями:
Рассмотрим это уравнение по участкам.
Первый
участок:
.
Крутящий момент имеет постоянную
величину, равную 2L=
ml
, т.е.
.
Второй
участок:
.
На этом участке крутящий момент изменяется
по линейному закону, поэтому достаточно
вычислить значения на концах второго
участка: 
,
.
Третий
участок:
.
На третьем участке крутящий момент
имеет постоянную величину минус 0,5ml.
Следует отметить, что в сечении z=2l
, где приложен сосредоточенный момент
L
, на графике имеет место разрыв функции
на величину этого момента.
Четвертый
участок:
.
Крутящий момент на этом участке изменяется
по линейному закону:
Эпюра
показана на рисунке 2.15 б.
Задача 5
Для
стержня (рис.2.16 а) построить эпюры
поперечных сил
и
изгибающих моментов
,
если
,
.
Определим
реакции опор. На опоре А в общем случае
возникают две реакции
и
.
Так как на стержень не действуют
горизонтальные силы, то из уравнения
получим реакцию
=0.
Предположим,
что реакции
и
положительные, т.е. совпадают с направлением
оси Y
. Из уравнения моментов относительно
опоры В находим реакцию
:
,
,
отсюда =0,75ql.
Из
уравнения моментов относительно опоры
А находим реакцию
:
,
,
отсюда
=1,75ql.
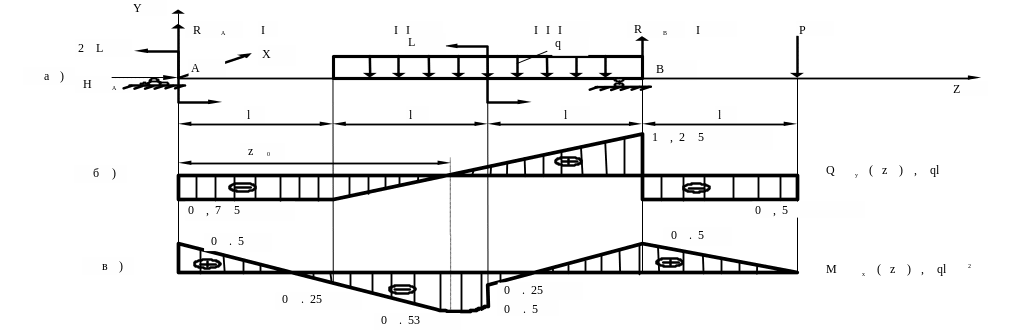
Рис.2.16
Так
как значения реакций
и
получились положительными, то их
направление выбрано верно.
Для проверки правильности найденных реакций используем второе уравнение статики:
,
следовательно, реакции определены верно.
Разбиваем
стержень на четыре участка. Запишем
уравнения поперечных сил
и изгибающих моментов
в произвольном сечении с абсциссой z
, ограничив участки вертикальными
линиями:
Для
поперечной силы Q
второй и третий участок объединены,
т.к. функция
в пределах второго и третьего участков
непрерывна. Уравнение
можно было получить путем дифференцирования
уравнения моментов
:
.
Рассмотрим
уравнения
и
по участкам.
Первый участок:
.
Поперечная сила на протяжении всего участка постоянна.
,
.
Изгибающий момент на этом участке изменяется по линейному закону, причем в начальном сечении, где приложен сосредоточенный момент, имеет место скачок на величину этого момента.
Второй участок: .
Поперечная сила на этом участке изменяется по линейному закону.
,
Изгибающий момент на втором участке изменяется по закону квадратной параболы:
,
.
Так
как поперечная сила в пределах второго
участка меняет знак (график пересекает
ось), то в точке
изгибающий момент принимает экстремальное
значение. Исследуем функцию
на втором участке на экстремум:
,
откуда
=1,75l.
Изгибающий момент в сечении принимает экстремальное значение:
.
Вогнутость
параболы определяется по правилу
«дождя», т.е. если
,
то парабола строится выпуклостью вниз,
а если
,
то выпуклостью вверх.
Третий участок:
,
,
,
.
Четвертый
участок:
.
Отметим,
что в сечении
на эпюре
имеет место разрыв на величину реакции
=1,75ql,
а в сечении
-
на величину силы Р.
,
.
По вычисленным значениям строим эпюру поперечных сил (рис.2.16 б) и эпюру изгибающих моментов (рис. 2.16 в).
Задача 6
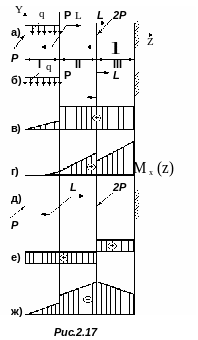
Для стержня, нагруженного в двух
взаимно перпендикулярных плоскостях
(рис. 2.17 а), построить эпюры поперечных
сил
и
и
изгибающих моментов
и
,
если P=2ql,
L=1,25q
.
Подобные задачи удобнее рассматривать в каждой плоскости с соответствующими внешними нагрузками отдельно. Рассмотрим вертикальную плоскость Y 0 Z (рис. 2.9 б).
Разбиваем стержень в этой плоскости на три участка и запишем уравнения и в произвольном сечении с абсциссой z .
Первый
участок:
,
,
,
.
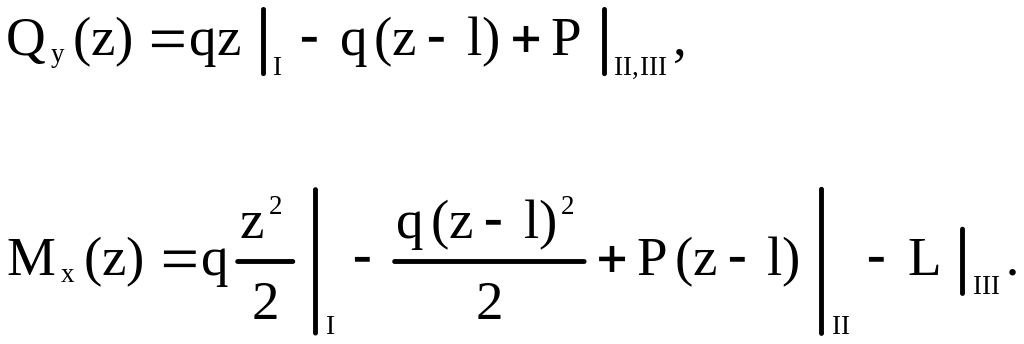
Второй
участок:
,
,
.
Третий
участок:
,
,
.
Следует
отметить, что в сечении
на эпюре
имеет место разрыв функции на величину
приложенной силы Р, а в сечении
на эпюре
-
на величину внешнего момента L.
По полученным данным строим эпюру
(рис. 2.17 в) и эпюру
(рис. 2.17 г).
1. Рассмотрим горизонтальную плоскость X0Z (рис. 2.17 д) и запишем уравнения и в произвольном сечении с абсциссой сечения z и рассмотрим их по участкам.
,
.
Первый участок:
,
,
.
Второй
участок: 
,
,
.
Третий
участок:
,
,
.
Отметим,
что в сечении
эпюра поперечных сил
имеет разрыв на величину приложенной
силы 2Р, а в сечении
эпюра изгибающего момента
–
на величину приложенного момента L.
По полученным значениям построены эпюры
(рис.2.17 е) и
(рис. 2.17ж).
Задача 7
Вал
круглого поперечного сечения диаметром
d
передаёт мощность
кВт, при
об/мин. Ведущий шкив I
имеет диаметр
=
0,3 м, ведомый шкив II
-
=
0,2 м, a =
0,7 м, b = 0,5 м.
Ветви ременной
передачи ведущего и ведомого шкивов
расположены во взаимно перпендикулярных
плоскостях. Силы натяжения в ведущих
ветвях принять равными удвоенным усилиям
в ведомых ветвях, т.е.
=2
и
=2
.
Составить расчетную схему и построить
эпюры внутренних силовых факторов.
При составлении расчетной схемы необходимо силы, приложенные к шкивам, привести к центрам тяжести сечений В и К.
Силы в сечении К приводятся к равнодействующей
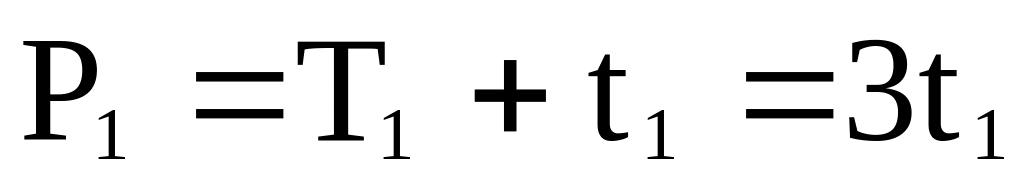и паре сил
,
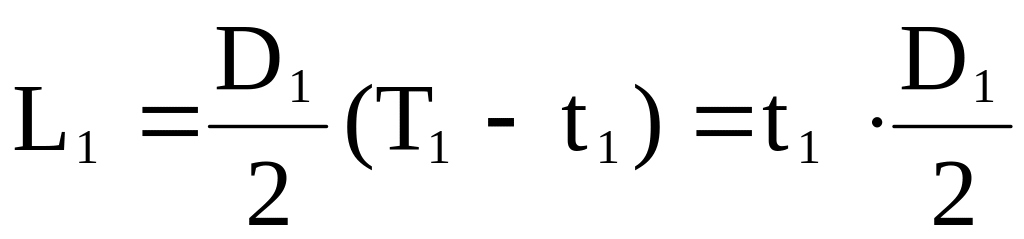в сечении В имеем соответственно
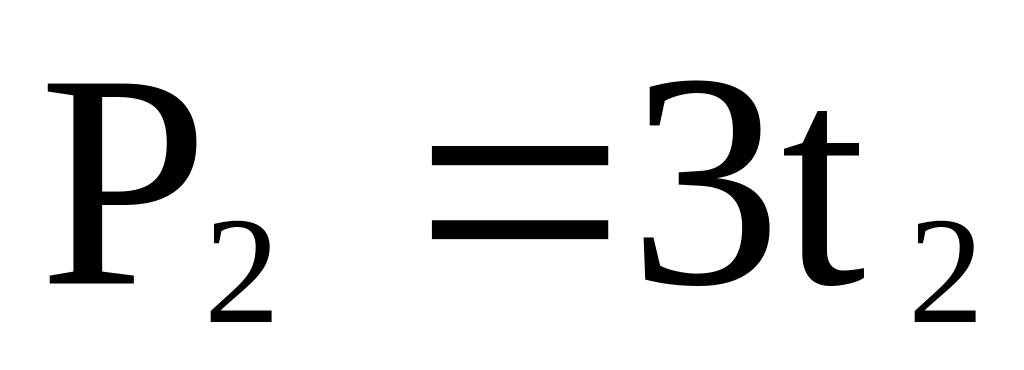и
.
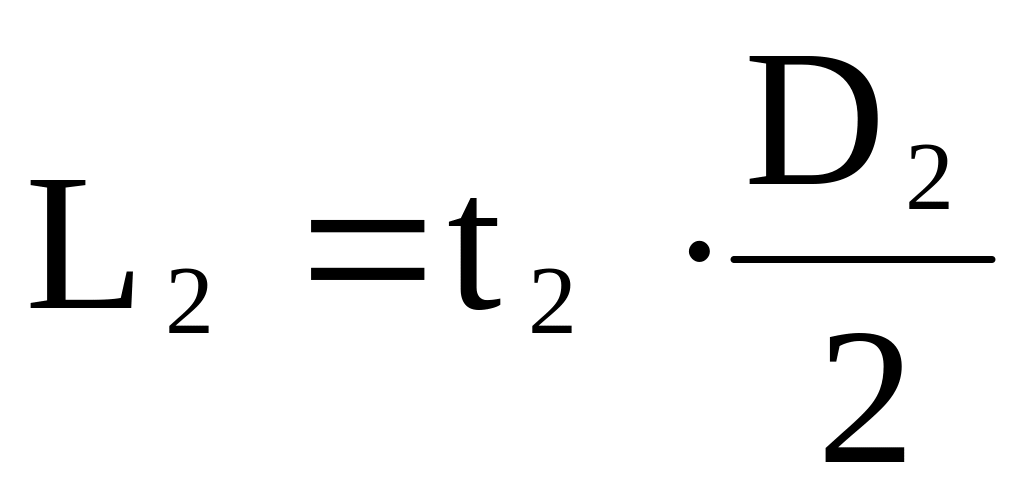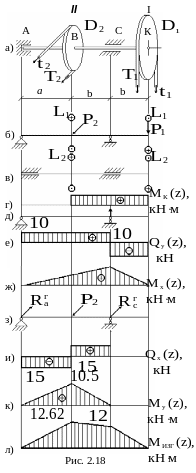
Расчетная схема вала показана на рис.
2.18 б Если в общем случае внешние силы
не лежат в вертикальной и горизонтальной
плоскостях, то их можно разложить на
вертикальные и горизонтальные
составляющие. 2.
2.
Для составления уравнений внутренних
сил и построения эпюр рассмотрим действие
только крутящих моментов
и
(рис.2.18 в). Крутящий момент определяется
по формуле:
,
где
L
– крутящий момент,
;
N
– мощность, кВт; n
– частота вращения вала, об/мин.
Т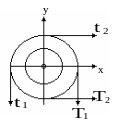
ак
как мощности на ведущем и ведомом валу
равны, то получим:
Уравнение
крутящих моментов для произвольного
сечения вала с абсциссой z
запишется
в виде
.
Таким образом, на участке вала от сечения
А до сечения В крутящий момент равен
нулю, а на участке от сечения В до сечения
К крутящий момент имеет постоянную
величину, равную
Эпюра
показана на рисунке 2.18г. Действие
поперечных нагрузок в вертикальной и
горизонтальной плоскостях рассмотрим
отдельно.
Вертикальная плоскость Y0Z
(рис.2.18 д).
В
вертикальной плоскости в сечении
действует сила
,
которую определим из вышеприведенной
формулы:
тогда
.
Определяем
реакции опор. Предположим, что
реакция
направлена вниз, а реакция
–
вверх. Сила
направлена перпендикулярно к оси
стержня, поэтому горизонтальная реакция
в опоре А
.
,
,
,
,
Реакции
получились положительными, следовательно,
их направление выбрано верно. Правильность
вычисленных значений
и
проверим, используя второе уравнение
статики:
,
,
10+3424
0.
Реакции определены верно.
Запишем уравнения и в произвольном сечении вала с абсциссой z.
,
.
I
участок:
.
Поперечная сила на этом участке постоянна и равна =10 кН. Изгибающий момент изменяется по линейному закону и в концевых точках:
,
II
участок:
.
Поперечная
сила на этом участке постоянная и равна
.
Изгибающий момент на этом участке в концевых сечениях участка будет таким:
,
.
Эпюры поперечной силы и изгибающего момента показаны на
рис. 2.18е и ж.
Горизонтальная плоскость X0Z (рис. 2.18 з).
В
горизонтальной плоскости в сечении
действует сила
,
которую определим по формуле
тогда
.
Определяем
реакции опор. Предположим, что реакции
и
совпадают с направлением оси X.
Реакция
.
,
,
кН.
,
,
кН.
Направление реакций выбрано верно, а численные значения проверим:
,
.
Реакции
вычислены правильно. Запишем уравнения
и
в произвольном сечении вала с абсциссой
z:
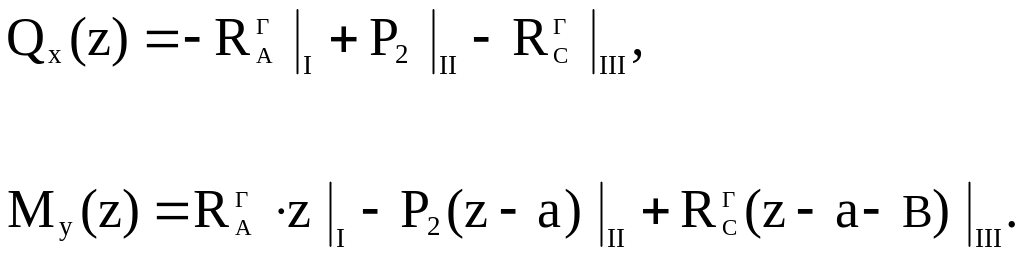
I
участок:
.
Поперечная
сила
на этом участке постоянна и равна
кН.
Изгибающий момент на этом участке
меняется по линейному закону и на концах
участка принимает значения:
,
кН.
II
участок:
Поперечная сила на этом участке постоянна и равна
кН.
Изгибающий момент меняется по линейному закону и равен в концевых сечениях участка:
,
.
III
участок:
.
На третьем участке поперечная сила и изгибающий момент равны нулю.
Эпюры и в горизонтальной плоскости показаны на рис. 2.18 и, к.
Для выявления наиболее нагруженного (опасного) сечения целесообразно построить эпюру результирующего изгибающего момента
.
Вычислим результирующий изгибающий момент в характерных сечениях А ,В, С, К.
,
,
,
.
По
этим значениям в условной плоскости
строим эпюру
(рис. 2.18 л).