2. Внутренние силовые факторы

1. Понятия упругости и пластичности

Опыты показывают, что под действием внешних нагрузок размеры и форма тела всегда изменяются, даже при малой величине нагрузки. Это явление называют деформацией.

При относительно малых нагрузках деформация исчезает после удаления вызвавшей ее нагрузки; такая деформация называется упругой. Способность тела восстанавливать свои размеры и форму после удаления нагрузки называют упругостью.

При больших нагрузках часть деформации не исчезает после удаления вызывающей ее нагрузки. Деформация, сохраняющаяся после удаления вызывающей ее нагрузки, называется остаточной или пластической. Способность материала воспринимать пластические деформации без разрушения называют пластичностью.

2.2 Основные допущения о свойствах деформируемых тел

При изучении поведения тел под действием внешних нагрузок, обычно производится схематизация рассматриваемых тел; учет всех реальных свойств невозможен. Например, теоретическая механика оперирует с абсолютно твердым телом, в то время как все реальные тела под действием внешних нагрузок деформируются. Деформируемым телам приписывают следующие основные свойства.

1. Непрерывность. Представим объем, занимаемый телом, заполненным веществом сплошь, без разрывов, т.е. не будем учитывать реальное строение тел из атомов.

При такой схематизации твердого тела нужно отказаться от вычисления сил взаимодействия между отдельными атомами вещества. Вместо этого необходимо рассматривать равнодействующие большого числа межатомных сил, действующих по какой-либо площадке, называя их внутренними силами.

Принятое допущение позволяет применять к исследованию деформации твердых тел методы анализа бесконечно малых величин.

2. Идеальная упругость. Принимается, что деформируемое тело испытывает только упругие деформации, являющиеся однозначной функцией нагрузок. В реальных телах наблюдаются некоторые неупругие явления (например, местные микроскопические пластические деформации), однако в большинстве случаев эффект их мал и его можно не учитывать.

3. Изотропность, т.е. одинаковость свойств по различным направлениям.

4. Однородность.

2.3 Расчетные схемы

Для расчета стержня составляют его расчетную схему, в которой показывают форму оси стержня, типы опор и внешние нагрузки, действующие на стержень.

По форме оси различают стержни с прямой, кривой и ломаной осью.

В процессе нагружения стержней их поперечные сечения получают перемещения, т.е. их положение в пространстве изменяется. Поворот поперечного сечения называют угловым перемещением, изменение положения центра тяжести - линейным перемещением.

Поперечные сечения стержня получают перемещения в результате движения стержня как жесткого тела (в этом случае перемещения всех поперечных сечений одинаковы) и деформации стержня. В последнем случае каждое поперечное сечение перемещается относительно других поперечных сечений.

Чтобы устранить движение стержня как жесткого тела, применяются устройства, называемые опорами и запрещающие перемещения некоторых сечений. Поперечное сечение, перемещения которого ограничены опорой, называют опорным сечением.

Наиболее часто встречаются следующие типы опор.

1. Шарнирно-подвижная, запрещающая одно линейное перемещение опорного сечения.

2. Шарнирно-неподвижная, запрещающая линейное перемещение опорного сечения в двух взаимно перпендикулярных направлениях (например, по вертикали и по горизонтали).

3. Защемляющая опора, запрещающая как линейные, так и угловые перемещения опорного сечения.

Изображения этих опор в расчетных схемах стержней показаны на рис. 2.1.

Внешними называют нагрузки, действующие на данное тело со стороны других тел. Существуют два типа внешних нагрузок: объемные и поверхностные. Объемными называют нагрузки, приложенные ко всем частицам объема тела (например, давление газа или жидкости на стенки сосуда, давление одной детали на другую по поверхности контакта).

В расчетных схемах стержней удобно относить нагрузки (как объемные, так и поверхностные) к единице длины стержня. Такие нагрузки называют погонными.

Погонные нагрузки характеризуются их интенсивностью - величиной нагрузки на единицу длины стержня. Размерность интенсивности погонной нагрузки - единица силы, поделенная на единицу длины. Интенсивность погонной нагрузки будем обозначать буквой q , в случае необходимости указывая индексом, какой оси параллельна погонная нагрузка.

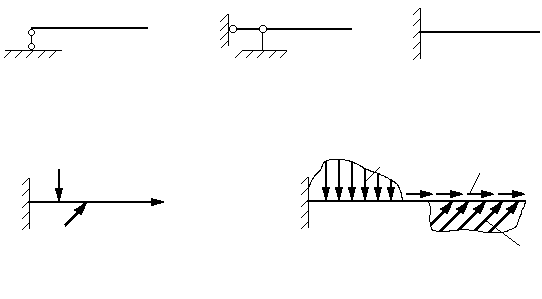
Рис. 2.1

Если длина площадки, по которой распределена погонная нагрузка, мала по сравнению с длиной стержня, нагрузку считают сосредоточенной в одной точке. Такие нагрузки называют сосредоточенными силами.

При составлении расчетной схемы стержня каждую нагрузку приводят к центру тяжести того поперечного сечения, в плоскости которого приложена эта сила.

Если к центру тяжести поперечного сечения приводится сосредоточенная сила, то в расчетной схеме стержня получим в общем случае силу и пару сил. Эту пару называют сосредоточенным моментом. Размерность сосредоточенного момента - единица силы, умноженная на единицу длины.

Если к центрам тяжести поперечных сечений приводится погонная нагрузка, то в расчетной схеме стержня получим погонную силовую и погонную моментную нагрузки. Погонная моментная нагрузка характеризуется ее интенсивностью - величиной момента на единицу длины стержня. Размерность интенсивности погонной моментной нагрузки - единица силы.

Изображение различных типов нагрузок в расчетных схемах стержней показано на рис. 2.2.

Рис. 2.2