Задача 4

Дана фигура, ограниченная линиями x+y=1 и x+2y=2. Вычислить ИХС S_x, S_y, I_x, I_y, I_xy, положение центра тяжести относительно осей, показанных на рис. 1.8.

Совместное решение уравнений позволяет найти координаты вершин треугольника: A(0;1), B(1;0), C(2;0).

1. Вычисляем площадь фигуры

Рис. 1.8

2.Вычисляем статические моменты фигуры относительно осей OX и OY(рис.1.8):

3. Вычисляем координаты центра тяжести O_c фигуры:

4. Вычисляем моменты инерции фигуры относительно осей OX и OY:

5. Вычисляем моменты инерции фигуры относительно центральных осей O_cX_c и O_cY_c, параллельных осям OX и OY. Используем формулы (1.17) параллельного переноса:

Задача 5

Для кругового сектора радиусом R с углом при вершине 2a определить моменты инерции относительно осей OX и OY (рис. 1.9).

Для осесимметричного сечения удобнее пользоваться полярной системой координат. Поэтому x=r ×cosj , y=r ×sinj , dF=rdj × dr.

Рассчитываем моменты инерции I_x и I_y:

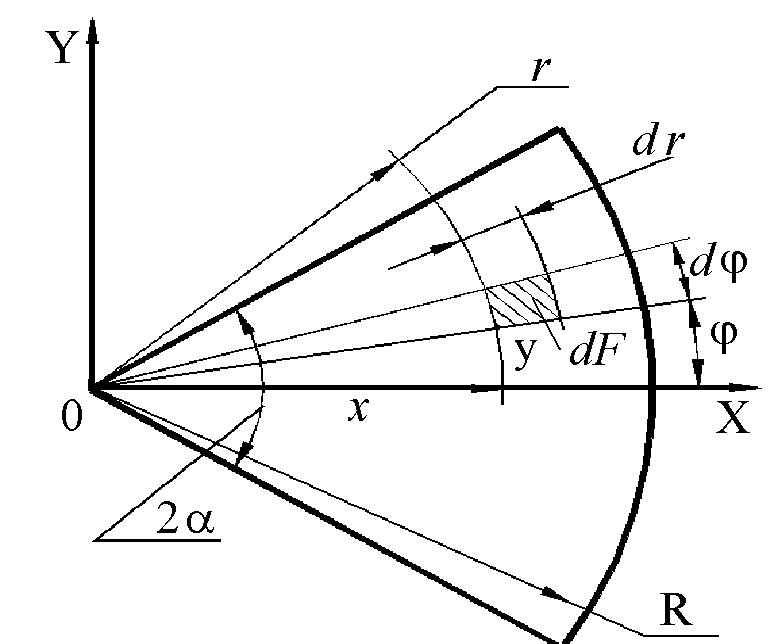
Рис. 1.9

Значения I_x и I_y имеют практическое применение при различных значениях угла при вершине сектора. При a=p=180° сечение круглое (рис. 1.10).

Ясно, что I_x=I_y,

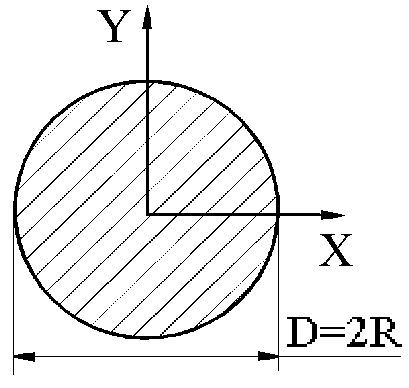
Рис. 1.10

При a=0.5×p=90° поперечное сечение - полукруг (рис. 1.11)

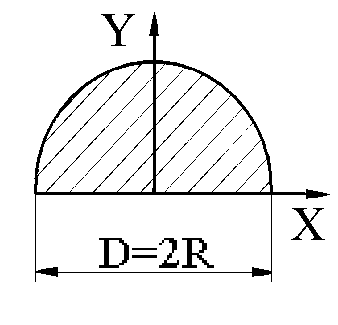
Рис. 1.11

Задача 6

Для криволинейного стержня, кривизна которого k, а поперечное сечение прямоугольное (рис. 1.12), определить ИХС A, B, C, положение центра упругости относительно главных центральных осей OX и OY.

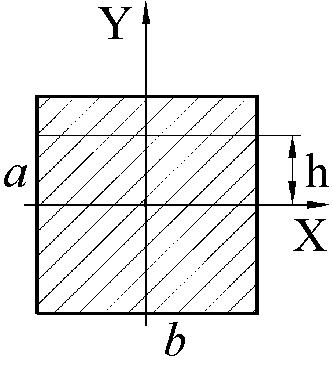
Рис.1.12

Здесь b=kh/2=h/2R; R – радиус кривизны продольной оси стержня; F=a× b – площадь прямоугольного поперечного сечения стержня.

Для стержня с прямой осью k=0 и, значит, b=0. Поэтому получим A=F, В=0,

Ординату центра упругости определяем как

Задача 7

Для заданного поперечного сечения (рис. 1.13) необходимо определить положение центра тяжести, главные центральные оси, величину главных моментов инерции.

1. Разделим исходную плоскую фигуру на две фигуры: прямоугольник 1 и полукруг 2.

2. Через центры тяжести фигур O₁ и O₂ проведём центральные оси каждой фигуры так, чтобы они были параллельны.

3. Определим площадь каждой фигуры и геометрические характеристики относительно её центральных осей.

Фигура 1 (прямоугольник): F₁=c×3c=3c², так как ось O₁Y₁ совпадает с осью симметрии сечения.

Фигура 2 (полукруг):

поскольку ось O₂Y₂ совпадает с осью симметрии сечения.

Формулы для вычисления моментов инерции могут быть получены указанными выше способами или взяты из справочной литературы, на- пример [19].

4. Для нахождения центра тяжести сечения выберем вспомогательную систему координат XOY. Координаты центров тяжести составляющих фигур 1 и 2 относительно этих осей будут O₁(2C;3,5C), O₂(2C;1,15C).

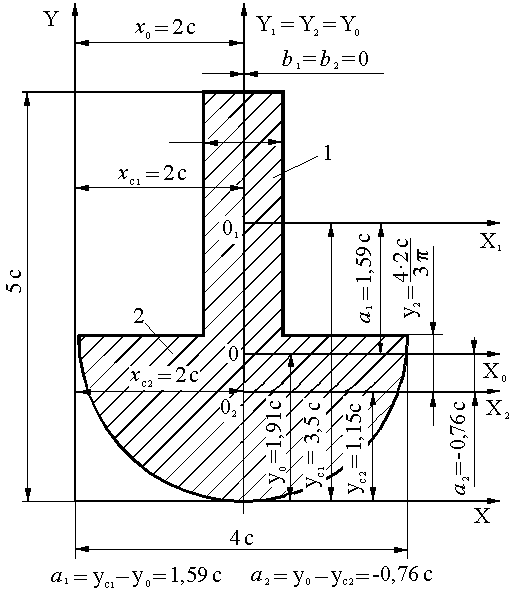
Рис. 1.13

Определим координаты центра тяжести всего сечения:

Через центр тяжести O сечения проведём оси OX₀ и OY₀ таким образом, чтобы

ось OY₀ совпала с осью симметрии сечения и, значит, с осями O₁Y₁ и O₂Y₂.

Оси OX₁ и OY₁ – главные центральные оси, так их начало координат совпадает с центром тяжести сечения, и одновременно центробежный момент ­, поскольку ось OY₀ совпадает с осью симметрии сечения.

5. Определим главные центральные моменты инерции сечения:

Задача 8

Поперечное сечение состоит из двух фигур: швеллера 1 (профиль № 18d, ГОСТ 8240-72) и уголка неравнобокого 2 (профиль № 12,5/8 d, ГОСТ 8510-72). Основные размеры, в миллимет- рах, положение центров тяжести O₁ и O₂ центральные оси O₁X₁, O₁Y₁, O₂ X₂ , O₂ Y₂ этих фигур показаны на рис. 1.14.

1. Из справочника [19], опре- делим основные интегральные характеристики сечений.

Фигура 1 (швеллер):

F₁=20,7 см², I_x1=1090 см⁴,

I_x1=86 см⁴, I_x1y1=0, так как ось O₁X₁ совпадает с осью симметрии швеллера.

Фигура 2 (уголок): F₂=23,4 см ², I_x2=117 см ⁴, I_y2=365 см ⁴ ,

I_v2=69,5 см ⁴, tga=0,400.

Рис. 1.14

2. Для нахождения центра тяжести всего сечения выбираем вспомогательные оси OX и OY, параллельные осям O ₁ X ₁ , O ₁Y ₁ , O ₂ X ₂ , O ₂ Y₂ .

Координаты центра тяжести поперечного сечения определим как

Через центр тяжести поперечного сечения О проведём центральные оси OX_c и OY_c, параллельные центральным осям фигур 1 и 2.

3. Определим моменты инерции сечения относительно центральных осей OX_c и OY_c. Предварительно вычислим центробежный момент инерции уголка относительно его центральных осей:

a = arctg(0,400)=21,8°.

Тогда

Теперь

4. Определяем величины главных моментов инерции

Таким образом, получим I₁=I_max=1754 см⁴, I₂=I_min=859 см⁴.

5. Определяем положение главных центральных осей OX₀ и OY₀:

a₁= arctg(– 0,1003 ) = – 5,27= 5,78°,

a₂= arctg( 9,8773 ) = 80,73= 84,22°.

Положение главных центральных осей OX₀ и OY₀ показано на рис. 1.14.

6. Проверка правильности решения.

а) в данном примере

см⁴ ;

б) в данном примере

1745×868 – ( – 89,7 ) ² = 1754×859 – 0 ;

в) tga₁×tga₂ = – 1, в данном примере

tg(– 5,78° )×tg( 84,22° ) = – 0.1003 × 9,8773 » – 1.

27