1.10. Интегральные характеристики сложных плоских фигур

Сложными будем считать плоские сечения, ИХС которых не могут быть вычислены, как для односвязного контура. Для фигуры (рис.1.4) любую ИХС можно получить алгебраическим суммированием ИХС простых фигур, составляющих исходную:

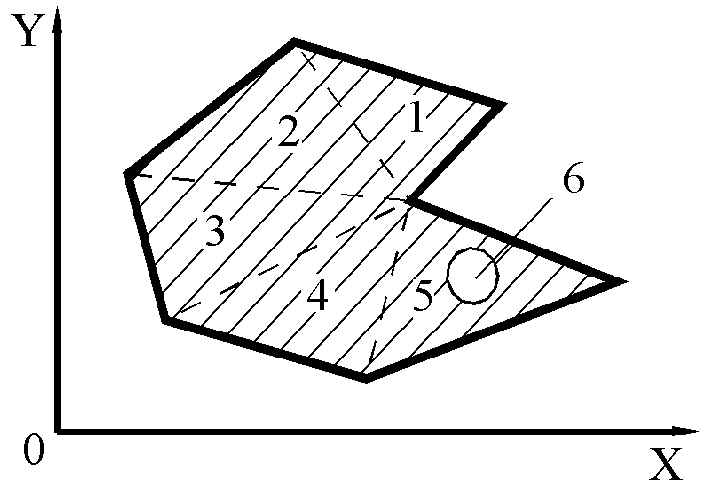
Рис. 1.4

1.11. Определение интегральных характеристик сечений стержней

с криволинейной осью

Известно [4], что нормальные напряжения в поперечном сечении стержня с криволинейной осью определяются по формуле

(1.32)

где E – модуль нормальной упругости; K=1/r – кривизна оси недеформированного стержня; r - радиус кривизны оси недеформированного стержня; y - расстояние от главной центральной оси сечения стержня до волокна, где вычисляются напряжения.

Из системы уравнений

определяют параметры а и с.

В системе (1.33) коэффициенты A, B, C являются ИХС заданной плоской фигуры, которые определяют как

(1.34)

(1.35)

(1.36)

Если в качестве осей координат выбрать главные центральные оси плоской фигуры, то между величинами A, B, C устанавливается простая зависимость:

(1.37)

Из уравнений (1.37) следует, что достаточно вычислить одну из величин В, А или С, как оставшиеся определяются однозначно. Эксцентриситет (ордината упругого

центра) плоской фигуры криволинейного стержня определяют по формуле

(1.38)

Из формул (1.34) – (1.36) видно, что если кривизна стержня k=0, то A=F, B=S_x , C=I_x .

Алгоритм определения центра тяжести сечения

и его главных моментов инерции

1. Разделить заданную фигуру на простые фигуры (т.е. такие фигуры, моменты инерции которых могут быть найдены по определению или даны в справочниках).

2. Выписать геометрические характеристики каждой из простых фигур (координаты центра тяжести, площадь, осевые и центробежный моменты инерции, угол, определяющий положение главных осей инерции данной фигуры).

3. Выбрать оси X, Y для определения координат центра тяжести всей фигуры (оси относительно которых можно просто определить координаты центра тяжести составляющих фигур).

4. Определить координаты x_i, y_i центров тяжести составляющих фигур относительно осей X, Y.

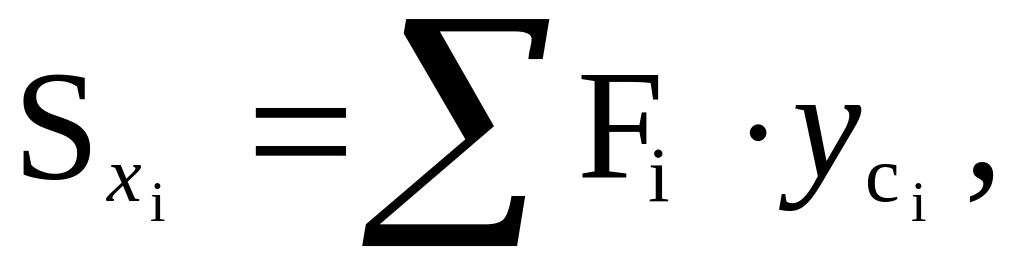
5. Определить статические моменты площади всей фигуры относительно осей X, Y: 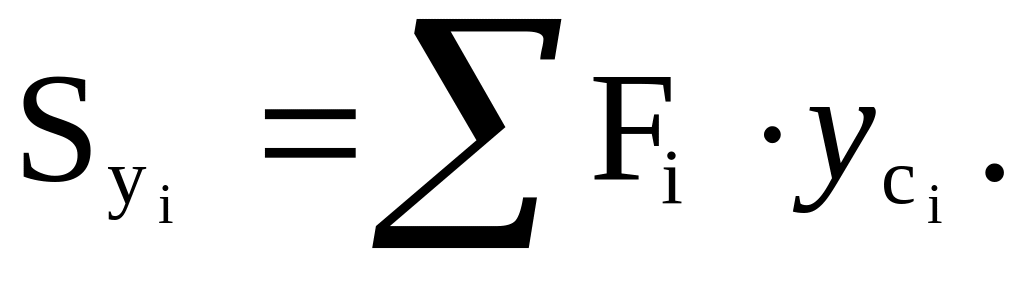Необходимо обратить внимание на знак координат x_ci , y_ci .

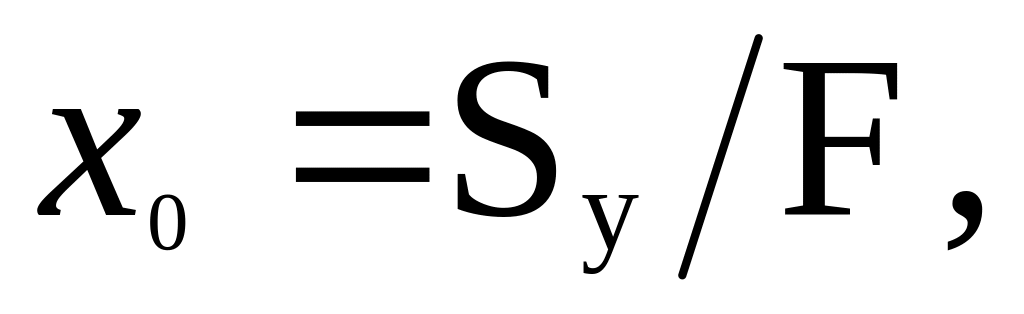
6. Определить координаты x₀ , y₀ центра тяжести всей фигуры относительно осей X, Y. _. Для контроля можно использовать правило: общий центр тяжести двух фигур лежит на отрезке, соединяющем их центры тяжести, и делит его на части, обратно пропорциональные площадям фигур.

7. Выбрать центральные оси всей фигуры. Эти оси целесообразно выбрать так, чтобы они были параллельны главным центральным осям инерции большинства составляющих фигур. Если фигура имеет ось симметрии, то одна из осей (X_сi или Y_сi) направляется по этой оси.

8. Определить осевые моменты инерции каждой из составляющих фигур относительно ее центральных осей, параллельных осям X₀, Y₀. В некоторых случаях удобнее сначала определить геометрические характеристики относительно осей X, Y, а затем выполнить параллельный перенос осей и найти моменты инерции относительно центральных осей X₀, Y₀. (Если главные центральные оси инерции данной фигуры не параллельны осям X₀, Y₀, нужно использовать формулы для моментов инерции относительно повёрнутых осей.)

9. Определить координаты центров тяжести составляющих фигур относительно центральных осей X₀, Y₀.

10. Определить осевые моменты инерции всей фигуры относительно осей X₀, Y₀. (Осевой момент инерции сложной фигуры относительно какой-нибудь оси равен сумме осевых моментов инерции составляющих фигур относительно той же самой оси. Осевой момент инерции фигуры относительно оси, параллельной её центральной оси, равен осевому моменту инерции данной фигуры относительно центральной оси, увеличенному на произведение площади фигуры на квадрат расстояния между осями.)

11. Определить центробежные моменты инерции каждой из составляющих фигур относительно ее центральных осей, параллельных осям X₀, Y₀. (Если известен центробежный момент инерции данной фигуры относительно других осей, не параллельных осям X_С, Y_С, необходимо использовать формулу центробежного момента инерции относительно повернутых осей.) При пользовании справочными данными необходимо обратить внимание на выбор положительного направления осей координат; при повороте координатных осей на угол 90° знак центробежного момента инерции изменяется.

12. Определить центробежный момент всей фигуры относительно осей X₀, Y₀. (Центробежный момент инерции сложной фигуры относительно какой-нибудь пары взаимно перпендикулярных осей равен сумме центробежных моментов инерции составляющих фигур относительно тех же осей. Центробежный момент инерции фигуры относительно осей, параллельных ее центральным осям, равен

центробежному моменту инерции относительно центральных oсей, увеличенному на произведение площади фигуры на координаты ее центра тяжести относительно новых осей.)

13. Определить положение главных центральных осей по формулам (1.22), (1.23).

14. Определить моменты инерции всего сечения относительно главных центральных осей инерции по формуле (1.21). Для контроля вычислений следует воспользоваться соотношениями (1.24).

Для приобретения устойчивых навыков по определению ИХС в прил. 1 приведены варианты индивидуальных заданий.