5. Определение осевых и центробежного моментов инерции

при повороте координатных осей

При повороте координатных осей OX и OY на угол a (рис. 1.2) координаты x₁ и y₁ элементарной площади dF относительно осей OX₁ и OY₁ определяются как

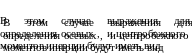
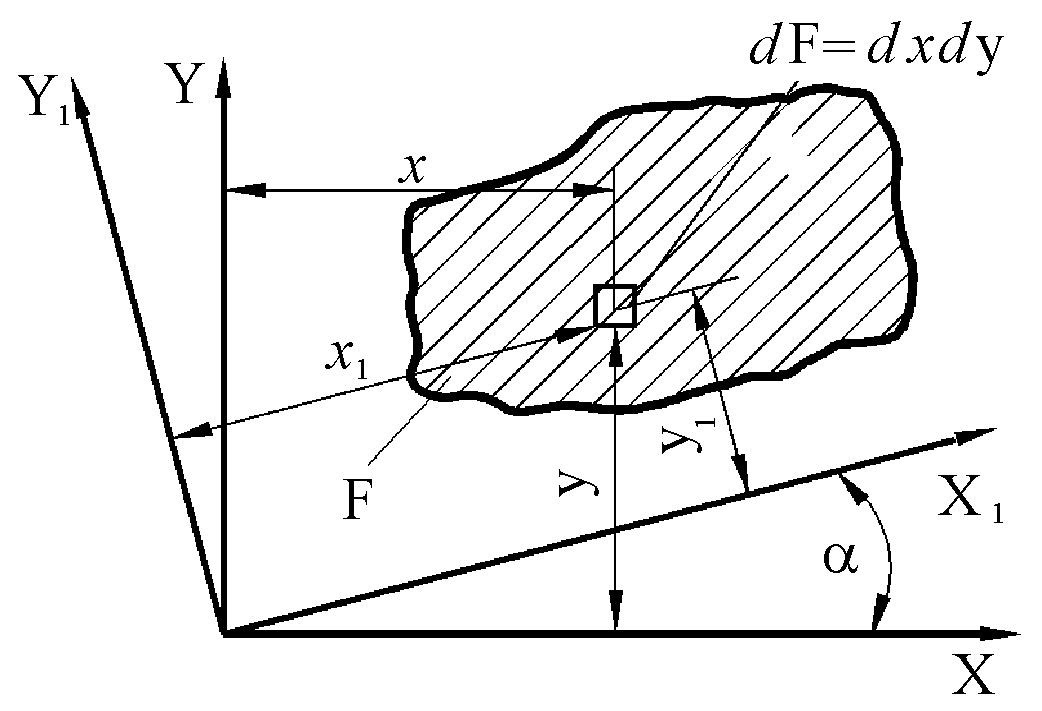
Рис.1.2

(1.18)

(1.19)

(1.20)

Из формул (1.18) – (1.20) следует, что при повороте осей OX и OY на 90°

Поскольку величина центробежного момента изменилась при повороте осей OX и OY на 90° от до минус , то, очевидно, что при некотором значении угла 0<a<90° центробежный момент инерции сечения будет равен нулю, а осевые моменты инерции примут максимальное и минимальное значения. Оси координат, относительно которых центробежный момент равен нулю, называют главными осями. Осевые моменты инерции, определённые относительно таких осей, называют главными моментами инерции. Если главные оси совпадают с центральными, то их называют главными центральными осями инерции. Осевые моменты сечения, определённые относительно главных центральных осей, называют центральными моментами инерции.

!!!!!1.6. Определение положения главных центральных осей и

главных моментов инерции сечения

Величину главных моментов инерции и положение главных осей можно определить из соотношений [4]

(1.21)

(1.22)

(1.23)

где D₁=I_x+I_y – первый инвариант моментов инерции; – второй инвариант моментов инерции; a₁, a₂ – углы поворота главных осей OX₁ и OY₁ относительно центральной оси OX.

Если центральные оси сечения обозначить OX_c Y_c , а главные оси - OX₀ Y₀, то из (1.18) , (1.19) , (1.23) после несложных преобразований получим

(1.24)

Выражение (1.24) используют, как правило, для проверки правильности решения задач.

7. Полярный момент инерции сечения

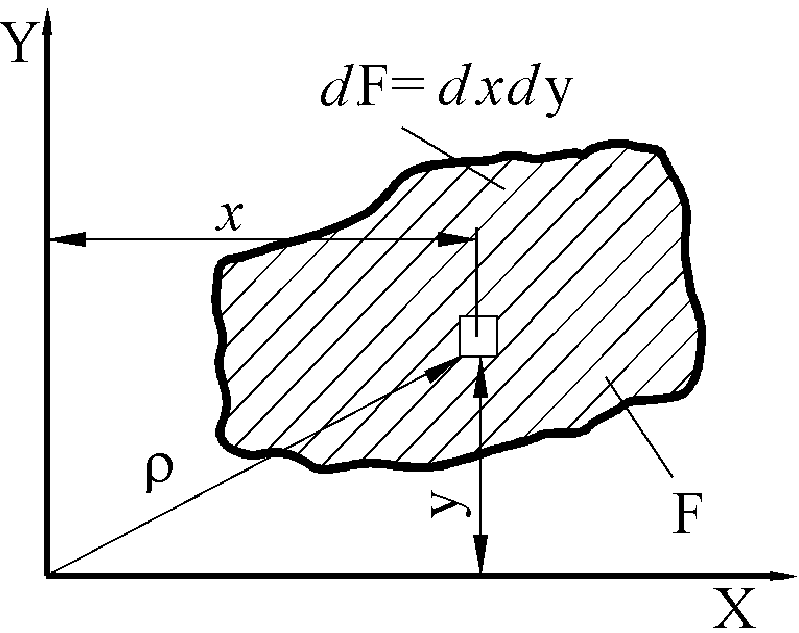
Рис. 1.3

Между полярным моментом инерции I_p и осевыми моментами инерции существует связь

(1.26)

1.8. Моменты сопротивления сечения

Осевым моментом сопротивления сечения называют отношение момента инерции относительно координатной оси к расстоянию от этой оси до наиболее уда­ленной точки поперечного сечения

(1.27)

Полярным моментом сопротивления называют отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения

(1.28)

Размерность моментов сопротивления сечений - единица длины в кубе.

1.9. Радиусы инерции сечения

Осевыми радиусами инерции сечения относительно осей OX и OY называют соотношения

(1.29)

где F – площадь поперечного сечения; I_x , I_y – моменты инерции относительно осей OX и OY.

Полярным радиусом инерции сечения относительно полюса называют выражение

(1.30)

Размерность радиуса инерции – единица длины.