1.1. Площадь и статические моменты сечений

Интегральная характеристика сечения, зависящая только от формы и размеров сечения, является площадью сечения и определяется как

(1.5)

Интегральные характеристики сечения, зависящие как от формы и размеров сечения, так и от его расположения относительно координатных осей, называют статическими моментами и определяют по формулам

(1.6)

(1.7)

Размерность статического момента - единица длины в кубе. В зависимости от выбора осей координат статические моменты могут принимать положительные и отрицательные значения, быть равными нулю.

1.2. Осевые и центробежный моменты инерции

Интегральные характеристики сечений, вычисляемые по формулам

(1.8)

(1.9)

называют осевыми моментами инерции сечения относительно осей OX и OY. Размерность осевого момента инерции сечения – единица длины в четвертой степени. Осевые моменты инерции всегда положительны и не равны нулю. Интегральная характеристика сечения, вычисляемая по формуле

(1.10)

называется центробежным моментом инерции сечения относительно двух взаимно перпендикулярных осей OX и OY. Размерность центробежного момента инерции - единица длины в четвертой степени. Центробежный момент может быть, как и статические моменты S_x, и S_y, положительным, отрицательным или равным нулю.

3. Определение интегральных характеристик сечений

при параллельном переносе осей

Предположим, что в системе координатных осей OX и OY известны такие ИХС плоской фигуры (рис. 1.1), как S_x, S_y, I_x, I_y, I_xy. Требуется определить одноименные ИХС относительно осей O₁X₁ и O₁Y₁, параллельных осям OX и OY. Известно также, что расстояние между осями OX и O₁X₁ равно "а", а между осями OY и O₁Y₁ –"b".

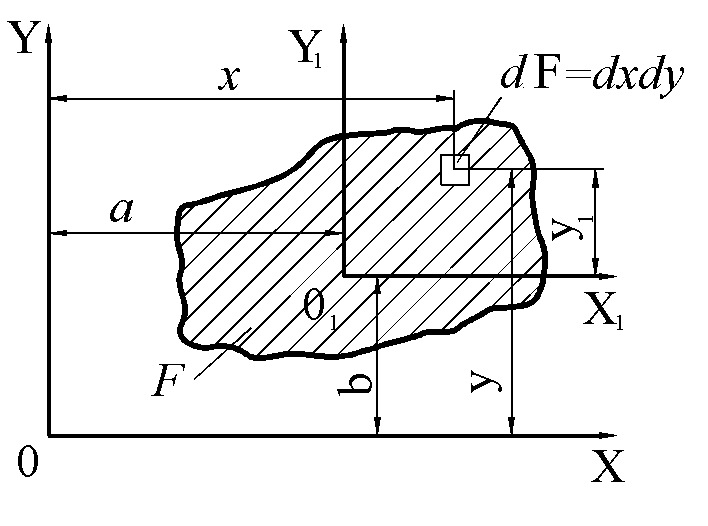
Рис. 1.1

(1.11)

(1.12)

Осевые и центробежные моменты сечения относительно осей O₁X₁ и O₁Y₁ :

(1.13)

(1.14)

(1.15)

4. Определение координат центра тяжести сечения

и положения центральных осей

Из формул (1.11), (1.12) следует, что при соответствующем выборе координатных осей O₁X₁ и O₁Y₁ статические моменты относительно них могут стать равными нулю. Оси, относительно которых статические моменты равны нулю, называют центральными осями, а точку пересечения таких осей – центром тяжести.

Координаты центра тяжести сечения относительно произвольно выбранных осей OX и OY определяют по формулам

(1.16)

Если сечение имеет ось симметрии, то эта ось всегда совпадает с одной из

центральных осей. Полагая, что оси OX и OY центральные, из (1.13) – (1.15) получим

(1.17)

Из первых двух формул (1.17) следует, что в семействе параллельных осей минимальный момент инерции получается относительно центральной оси ( a = 0 или b = 0). Поэтому при переходе от центральных осей к нецентральным осевые моменты инерции увеличиваются, и величины a² F и b² F следует к моментам инерции прибавлять, а при переходе от нецентральных осей к центральным – вычитать.

При вычитании центрального момента инерции по формулам (1.17) следует учитывать знак величин a и b.