5.9 Алгоритми пошуку несправностей в об’єктах.

Вид алгоритму (програми) пошуку несправностей істотно впливає на ефективність процесу контролю і діагностики. При розробці алгоритму пошуку зазвичай вирішують два завдання:

• визначають якнайкращий набір контрольованих параметрів;

• отримують якнайкращу послідовність вимірювання контрольованих параметрів.

Розглянемо найбільш поширені алгоритми пошуку несправностей в апаратурі.

Комбінаційний алгоритм. При завданні моделі системи з урахуванням її структури необхідна кількість контрольованих параметрів може бути скорочене із-за наявності послідовних, паралельних і зустрічно-паралельних (зворотних) зв'язків між елементами і групами елементів, наявність розгалужених виходів елементів, а також унаслідок того, що вірогідність одиночних дефектів в системі більше вірогідності кратних (одночасних) дефектів. У системах, в яких взаємозв'язані функціональні елементи, як правило, використовується комбінаційний алгоритм діагностування. Пошук дефекту проводять шляхом вимірювання певної сукупності контрольованих параметрів і на основі аналізу даних вимірювань роблять висновок про дефектний елемент.

Несправний елемент на основі функціональної моделі визначається шляхом аналізу матриці (таблиці) несправностей моделі.

При використанні комбінаційного алгоритму для реалізації

процедури діагностики вивід про стан об'єкту діагностики роблять після отримання інформації про всю сукупність діагностичних параметрів.

Послідовний алгоритм. При використанні цього алгоритму пошуку дефекту інформація про стан елементів аналізується по черзі по кожному елементу. Послідовний метод може бути реалізований за допомогою жорсткої або гнучкої програми. Жорстка програма передбачає незмінну послідовність аналізу, при використанні гнучкої програми пошуку порядок кожної подальшої перевірки залежить від результатів попередньої перевірки.

Один з найбільш поширених алгоритмів пошуку несправностей, що враховують структуру об'єкту, - алгоритм половинного розбиття. Він заснований на припущенні про рівнозначність відмов, що еквівалентно припущенню про послідовну схему з'єднання елементів.

Розглянемо систему з N послідовно сполучених елементів. Завдання пошуку несправного елементу в даному випадку полягає в знаходженні такої послідовності перевірок, при якій на пошук дефекту витрачається мінімум часу. Оптимізація програми пошуку дефекту полягає в тому, що при першому кроці весь ланцюжок елементів розбивається на дві частини так, щоб з вірогідністю 0.5 несправний елемент знаходився зліва або справа деякої контрольної точки. У цій точці здійснюється контроль стану лівого або правого ланцюжка елементів. Наявність або відсутність сигналу визначає напрям подальшого ділення на відрізки одної або іншої половини ланцюжка (з рівними значеннями вірогідності вказаних відрізків ланцюга елементів).

При контролі системи, що складається з N елементів з однаковою вірогідністю відмови, кожна перевірка розділяє об'єкт діагностики на дві частини з п і (N- п) числом елементів.

Середнє число елементів в тій частині, де опиниться елемент, що відмовив (зліва і справа точки ділення), рівно:

,

де - вірогідності того, що елемент, який відмовив, опиниться відповідно в першій чи другій частині об’єкта.

Отже:

.

Максимальне число т буде рівне N/ 2, тобто саме при половинному розбитті досягається мінімальне число перевірок. Максимальне число перевірок т прі використанні цього методу визначається з співвідношення N = 2^m, тобто m = lgN/lg2.

Максимальне число перевірок у разі безсистемного пошуку дефекту рівне N-1. При N= 100 відношення (N- 1) /m = 12,8.

Із збільшенням складності об'єкту цей виграш в скороченні максимального числа перевірок зростає.

Алгоритм половинного розбиття, як правило, використовується при послідовному з'єднанні елементів системи, оскільки в цьому випадку не треба будувати матрицю несправностей.

Найбільш загальний, оптимальний алгоритм пошуку несправності в складних системах може бути отриманий на основі інформаційного підходу з використанням матриці станів.

Пошук несправностей при такому підході починається в точці функціональної діагностичної моделі, для якої має місце співвідношення: , де - вірогідність перебування системи в j – му стані.

Алгоритм пошуку несправності на основі інформаційного підходу складається таким чином. По функціональній діагностичній моделі системи, для якої формується алгоритм, будується транспонована матриця станів (у рядках вказані перевірки z_j в стовпцях - стани S_j). Для кожного рядка z_j обчислюється функція переваги - W_j. Якщо відомості про вірогідності станів системи відсутні, то функція переваги для j – го рядка знаходиться як абсолютна величина різниці одиниць і нулів в цьому рядку.

Як перша перевірка вибирається та, для якої функція переваги W_j має найменшу величину. Далі перевірки здійснюються по двох майже рівноінформативних гілках. Для результатів z_j(W_min) = 0 і z_j(W_min) = 1 будуємо нові матриці, в які включають стани S_j , відповідні одиниці і нулю.

Процедура ділення матриці станів триває до виявлення елементу, що відмовив. В процесі ділення матриці можуть містити рядки з однаковими елементами. Проте такі рядки (перевірки) ніякої інформації про місце відмови не несуть і можуть бути викреслені перед подальшим діленням матриці.

Для побудови алгоритму пошуку несправностей може бути використана як повна матриця одиночних дефектів (матриця станів), так і мінімізована матриця, причому остання дозволяє побудувати алгоритм по мінімальній сукупності діагностичних параметрів.

Найкомпактніше алгоритм пошуку несправностей може бути

представлений у вигляді дерева логічних можливостей (ДЛМ). Візьмем для прикладу слідуючу функціонально – структурну схему об’єкта діагностування (рис.5.4). Дерево логічних можливостей, яке відповідає алгоритму пошуку несправностей для даного об’єкта зображено на

рис. 5.5.

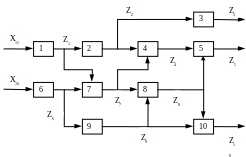
Рис. 5.4 Функціонально – структурна схема об’єкта діагностування

Об’єкт працезд.

Рис. 5.5 Дерево логічних можливостей

Комбінаторними характеристиками ДЛМ є сумарна довжина

всіх його гілок К_∑ і середня довжина гілки k_сер .