8.2. Метод Рунге - Кутта

Метод приближенного интегрирования дифференциального урав­нения (8.1), предложенный Рунге и усовершенствованный Куттом, ос­нован на том, что приращение искомого решения на каждом шаге интегрирования представляется в виде линейной комби­нации

с постоянными коэффициентами некоторых функций

j=1,2,…,m,

где h - шаг интегрирования,

a и - некоторые постоянные коэффициенты.

Рассмотрим одну из схем метода Рунге - Кутта, имеющую поря­док абсолютной погрешности на каждом шаге , то есть . Будем искать приближенное значение решения уравнения (8.1) в узле , через известное уже значение этого решения в предыдущем

(8.5)

узле по формуле

(8.5)

где

(8.6)

В свою очередь

(8.7)

Эта наиболее распространенная схема имеет следующее толкова­ние. На каждом шаге интегрирования сначала вычисляется направление поля в точке

и строится отрезок с этим направлением (рис 8 2). Затем нахо­дится середина отрезка и определяется направление поля в этой точке

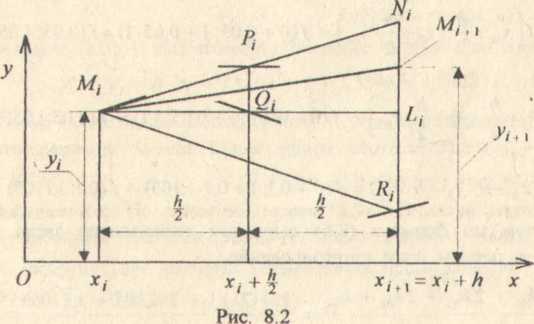
После этого же строится отрезок с направлением поля в точке находится середина этого отрезка и вычисляется направление поля в этой точке

Затем строится отрезок с направлением поля в точке и вычисляется направление поля в точке

Наконец, звено ломаной Эйлера, аппроксимирующее интегральную кривую на частичном отрезке строится в направлении, равном средне взвешенному значению направлений поля в точ­ках

и , вычисляемому по формуле (8.6).

Пример 8.2. По условиям примера 8.1 вычислить по методу Рунге - Кутта приближенные значения решения дифференциального уравнения в узлах и .

Решение. Так как в рассматриваемом случае f(x,y) = х + у,

h = 0,1, и то для нахождения решения в узле по­ложим i = 0 и по формулам (8 7), получим

Затем по формуле (8.6) вычислим направление звена ломаной Эйлера на первом шаге интегрирования

и по формуле (8.5) найдем значение приближенного решения в первом узле:

Чтобы подсчитать приближенные значения решения заданного дифференциального уравнения в следующем узле , положим i = 1 и по формулам (8.7) получим

Теперь по формуле (8.6) вычислим направление звена ломаной Эйлера на втором шаге интегрирования

а по формуле (8.5) - приближенное значение решения во втором узле:

Таким образом, по методу Рунге - Кутта приближенные значения искомого решения задачи Коши равны соответственно и

Задание 8.2. По условиям задачи 8.1, используя метод Рунге - Кутта, подсчитать значения решения задачи Коши в узлах и , сохраняя при расчетах четыре знака после запятой.

Ответ. , .