7.2. Преобразование интегральных уравнений в дифференциальные

При решении некоторых задач сначала составляется так называе­мое интегральное уравнение, то есть уравнение, в котором неизвестная функция находится под знаком интеграла, а затем путем дифференци­рования удается преобразовать это уравнение в дифференциальное.

Простейшие интегральные уравнения могут быть получены, на­пример, когда используются геометрический смысл определенного ин­теграла как площадь криволинейной трапеции и другие интегральные формулы (длина дуги, площадь поверхности, объем тела, работа силы и т. д.).

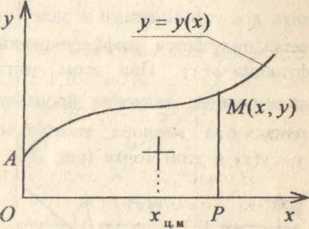
Пример 7.2. Найти кривую, лежащую в первой четверти, у кото­рой абсцисса центра масс криволинейной трапеции, ограниченной ося­ми координат, этой кривой и ординатой любой ее точки, равна трем четвертям абсциссы этой точки.

Решение. На кривой у = у(х) зафиксируем произвольную точку М(х,у) и опустим из нее перпендикуляр МР на ось Ох

(рис. 7.1). Абсцисса центра масс криволинейной трапеции ОАМР может быть вычислена по формуле где - статический момент инерции этой криволинейной трапеции относительно оси Оу, a S - ее площадь, которые, в свою очередь, могут быть найдены как

Согласно условиям задачи

, или .Подставляя в это соотношение вы­ражения для РИС 7.1

и S, получим ин­тегральное уравнение

Продифференцируем это уравнение по переменной х:

Еще раз продифференцировав последнее уравнение по х, полу­чим дифференциальное уравнение относительно функции

у =у(х):

Разделяя переменные, найдем решение этого уравнения.

Таким образом, условиям задачи удовлетворяет семейство пара­бол у = Сх².

Задание 7.2. Найти кривую, проходящую через точку

и обладающую следующим свойством: если через любую точку этой кри­вой провести две прямые, параллельные координатным осям, до пере­сечения с последними, то полученный при этом прямоугольник делит­ся кривой на две части, из которых одна, примыкающая к оси Ох, по площади вдвое больше другой.

Ответ: у² = 25х .

7.3. Решение геометрических задач

Для решения геометрических задач необходимо по ее условиям построить чертеж, обозначить искомую кривую через у = у(х) и выра­зить все упоминаемые в задаче величины через х, у и у', в результате чего получается дифференциальное уравнение относительно искомой функции у(х). При этом часто используется геометрический смысл

Рис 7.2

производной: значение производной в точке

равно тан­генсу угла наклона касательной, проведенной к графику функции у = у(х) в этой точке (рис 7.2), то есть

Для составления дифферен­циального уравнения при реше­нии геометрической задачи также могут быть использованы уравне­ния касательной

(7.4)

и нормали

(7.5)

проведенные к кривой у = у(х) в

точке

При решении геометрических задач применяется следующая тер­минология. Под длиной касательной к кривой

у = у(х) понимается длина отрезка касательной от точки касания до точки А пе­ресечения ее с осью абсцисс (рис 7.2), а проекция АР этого отрезка на ось Ох называется подкасателъной. Рис 7.3

Аналогично, под длиной норма­ли к кривой

у = у(x) в точке понимается длина отрезка нормали от точки до точки В пересечения ее с осью абсцисс, а про­екция PB этого отрезка на ось Ох называется поднормалью. И, нако­нец, перпендикуляр , опущенный из точки на ось абсцисс, называется ординатой точки касания.

Пример 7.3. Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная а².

Решение. Изобразим на чертеже некоторую кривую у = у(x) (рис. 7.3), зафиксируем на ней

произвольную точку М(х,у), проведем в этой точке касательную AM до пересечения с осью Ох и опустим перпендикуляр MB из точки М на ось Ох. В построенном таким обра­зом прямоугольном треугольнике АМВ, площадь S которого по усло­виям задачи равна а², катет MB равен модулю ординаты точки М, то есть так как точка М может лежать как выше, так и ни­же оси Ох, а угол есть угол наклона касательной к кривой у = у(х) в точке М. Согласно гео­метрическому смыслу производной

tgα = ± у'(х),

где учтено, что касательная AM может образовывать с осью Ох как острый, так и тупой угол. Тогда второй катет АВ рассматриваемого треугольника будет равен

а площадь треугольника -

откуда получим дифференциальное уравнение относительно искомой Функции у = у(х):

.

После разделения переменных и интегрирования

найдем интеграл этого дифференциального уравнения или то есть условиям поставленной задачи удовле­творяет семейство кривых

Задание 7.3. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньше абсциссы точки касания.

Ответ: у = Сх².