6.5. Особое решение дифференциального уравнения как огибающая семейства интегральных кривых

В заключение выясним геометрический смысл особого решения дифференциального уравнения

F(х,у,у') = 0, (6.25)

введя предварительно некоторые понятия.

Рассмотрим уравнение

Ф(х,у,С) = 0, (6.26)

где С – некоторый параметр. При этом каждому значению со­ответствует уравнение , определяющее на плоскости Оху некоторую кривую.

Множество всех кривых, определяемых уравнением (6.26), назы­вается однопараметрическим семейством кривых, а уравнение (6.26) называется уравнением этого семейства.

Так уравнение у = х + С определяет семейство прямых с угловым

коэффициентом, равным единице, а уравнение х² + у² = С - семейство концентрических окружностей с центром в начале координат.

Огибающей однопараметрического семейства кривых (6.26) назы­вается кривая, которая в каждой своей точке касается некоторой от­личной от нее кривой семейства и каждого куска которой касается бесчисленное множество различных кривых семейства.

Чтобы установить правило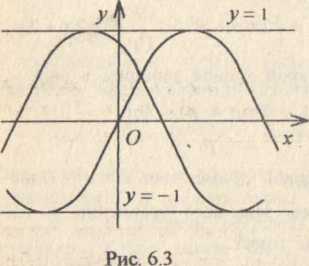

Например, семейство кубиче­ских парабол имеет огибающую у = 0

(рис 6.2), а се­мейство синусоид

у = sin (х + С) имеет огибающую, состоящую из двух прямых у = ± 1 (рис. 6.3).

Однако не всякое однопара­метрическое семейство кривых име­ет огибающую. Так, рассмотренные ранее семейства

у = х + С и х² + у² - С огибающих не имеют.

Чтобы установить нахождения огибающей семейства (6.26)

, прежде всего определим угловой коэффициент касательной к линии этого семейства.

Дифференцируя (6.26) и учитывая при этом, что у является функцией от х, а С = const, получим

откуда

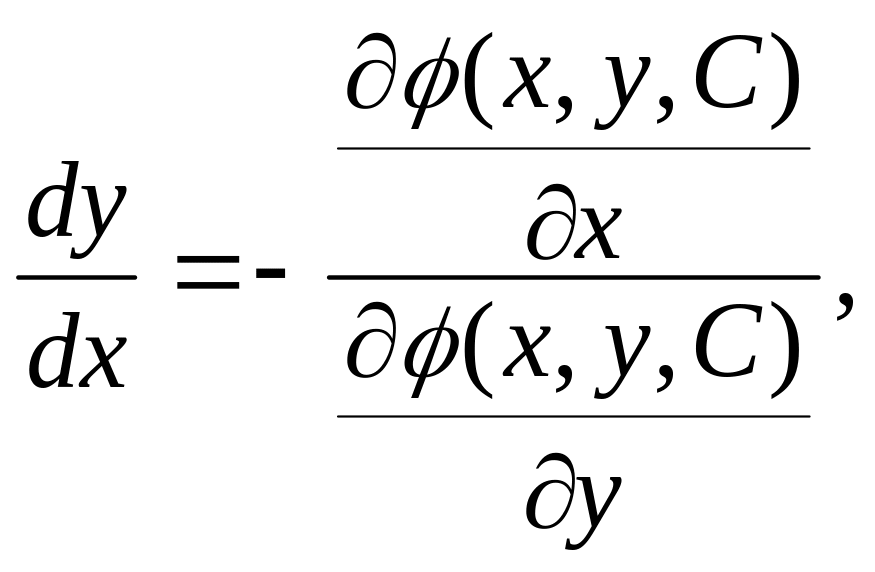(6.27)

считая при этом, что

Положим, что искомое уравнение огибающей будет

R(x,y) = 0. (6.28)

А поскольку любую функцию R(x, у) можно преобразовать к виду

R(x,y) = Ф(х,у,С),

где С = С(х,у) - некоторая функция от х и у, то можно считать, что левая часть уравнения (6.28) имеет вид (6.26), где С = С(х,у)

В свою очередь, неизвестную функцию С(х,у) определим из условия равенства угловых коэффициентов касательных к огибающей и линиям семейства (6.26)

Беря дифференциал от обеих частей равенства (6.26) и учиты­вая, что С = С(х,у), получим

(6.29)

Угловой коэффициент касательной к огибающей будет равен уг­ловому коэффициенту касательной к линии семейства (6.27) в том случае, если в (6.29) третье слагаемое будет равно нулю, то есть

Если считать dC = 0, то это дает С = const, то есть не огибаю­щую, а кривую семейства, и, следовательно, чтобы получить огибаю­щую, следует положить

Последнее уравнение и определяет функцию С = С(х, у), подстав­ляя которую в левую часть равенства (6.26), получим искомое уравне­ние огибающей (6.28). Таким образом, уравнение огибающей может быть получено исключением С из системы двух уравнений

(6.30)

Система уравнений (6.30) задает в параметрическом виде кривую, которая называется С-дискриминантной кривой. Следует заметить, что система (6.30) определяет только необходимые условия существования огибающей, достаточные же условия существования огибающей форму­лируются следующей теоремой: для того, чтобы С-дискриминантная кривая однопараметрического семейства кривых (6.26) была огибаю­щей, достаточно, чтобы вдоль этой кривой существовали частные производные и , из которых одна отлична от нуля.

Таким образом, чтобы найти огибающую, нужно найти уравнение С-дискриминантной кривой путем исключения С из системы уравнений и проверить выполнение достаточных условий.

Вернемся, наконец, к вопросу о геометрическом смысле особого решения дифференциального уравнения (6.25). Пусть теперь уравнение (6.26) описывает однопараметрическое семейство интегральных кривых дифференциального уравнения (6.25). Тогда можно сделать следующий важный вывод если однопараметрическое семейство интегральных кри­вых (6.26) дифференциального уравнения (6.25) имеет огибающую, то эта огибающая является особым решением данного уравнения.

Действительно, в каждой своей точке огибающая касается неко­торой интегральной кривой. Следовательно, в каждой такой точке оги­бающей значения х, у и у' удовлетворяют дифференциальному уравне­нию (6.25), то есть огибающая семейства интегральных кривых сама является интегральной кривой. Далее, в каждой точке огибающей на­рушена единственность решения, так как через нее в одном и том же направлении проходят две интегральные кривые — сама огибающая и одна из интегральных кривых семейства.

Сделанный вывод позволяет находить особое решение дифферен­циального уравнения как уравнение огибающей семейства интегральных кривых, описывающих его общий интеграл.

Пример 6.8. Найти особое решение уравнения

Решение. Интегрируя исходное уравнение, найдем его общее решение у = (х + С)³. Тогда согласно (6.26) имеет место Ф(х,у, С) = у - (х + С)³ и , а уравнение

С-дискриминангной кривой запишется в виде

откуда у = 0. На линии у = 0 имеет место

следовательно, прямая у = 0 является огибающей семейства интеграль­ных кривых, а функция у = 0 - особым решением исходного уравне­ния, что и было получено ранее при решении примера 6.3 иным спо­собом.

Задание 6.5. Найти особое решение уравнения

как огибающую семейства интегральных кривых.

Ответ. 4у = х².