Тема 2. Технические средства измерений электрических величин. Урок 1. Магнитоэлектрические приборы и их применение.

М агнитоэлектрические приборы (МЭП), как и любые электромеханические измерительные приборы, состоят из трех основных преобразователей: измерительной цепи (ИЦ) измерительного механизма (ИМ) и отсчетного устройства (ОУ).

Рис. 2.1. Структурная схема электромеханического измерительного прибора.

Конструктивно измеритель­ный механизм может быть выполнен либо с подвижным магнитом, либо с подвижной катушкой. На рис. 2.2 показана конструкция прибора с подвижной катушкой.

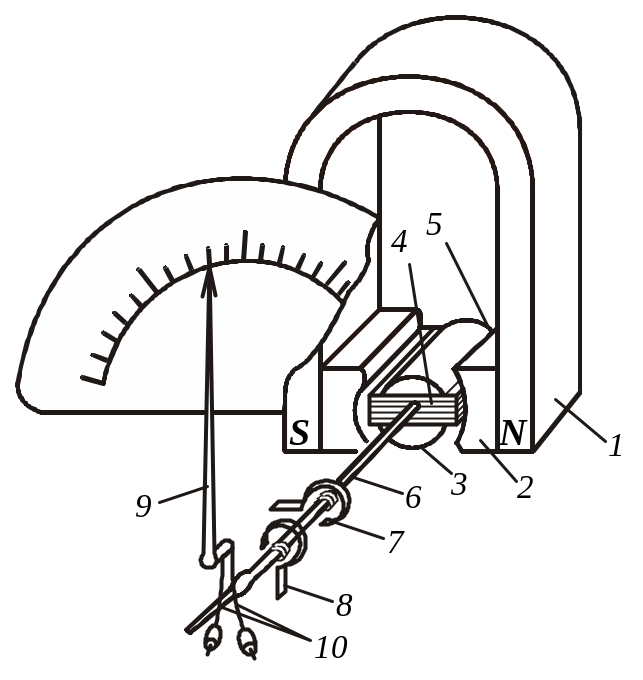
Рис.2.2. Устройство магнитоэлектрического прибора.

Постоянный магнит 1, магнитопровод с полюсными наконечниками 2 и неподвижный сердечник 3 составляют магнитную систему механизма. В зазоре между полюсными наконечниками и сердеч­ником создается сильное равномер­ное радиальное магнитное поле, в ко­тором находится подвижная прямо­угольная катушка 4, намо­танная медным или алюминиевым проводом на алюминиевом каркасе (применяют и бескаркасные рамки). Катушка (рамка) может поворачиваться в зазоре на полуосях 5 и 6. Спиральные пружины 7 и 8 создают противодействующий момент и используются для подачи измеряемого тока от выходных зажимов прибора в рамку. Рамка жестко соединена со стрелкой 9. Для балансировки подвижной части имеются передвижные грузики 10.

Принцип действия МЭП. Проходя по проводникам обмотки рамки, ток I взаимодействует с магнитным потоком постоянного магнита, что вызывает появление механических сил F, создающих вращающий момент Мвр для рамки. Из теоретических основ электротехники известно выражение для механической работы, совершаемой при перемещении проводника с током в магнитном поле:

F dα = dW_М ,

где F— сила, действующая на проводник в направлении элементарного перемещения

dα; dW_М - изменение запаса энергии магнитного поля.

Если проводник движется по окружности с радиусом r, то

dx=r dα,,

где dα — элементарный угол поворота.

Следовательно,

Fdα=dW_{М .}

Здесь F_r— вращающий момент - М_ВР, т. е.

М_ВР dα = dW_М .

Тогда окончательно запишем:

М_ВР = dW_М / dα. (2.1)

Это уравнение является обобщенным выражением вращающего момента для всех приборов, в которых используют сила электромагнитного поля.

Противодействующий момент в приборах необходим для создания однозначного соответствия измеряемой величины определенному углу отклонения подвижной части. В аналоговых электромеханических приборах противодействующий момент создается либо при помощи спиральных пружин (растяжек и подвесов), либо за счет энергии электромагнитного поля (в логометрах).

В случае, когда противодействующий момент соз­дается спиральной пружинкой

М_ПР = W·α, (2.2)

где W – удельный противодействующий момент, зависящий от геометрических размеров и материала пружины (растяжек)

Уравнение шкалы. Выражение для вращающего момента, действующего на рамку при протекании по ней тока I, мо­жет быть получен, исходя из обобщенного выражения вращаю­щего момента (2.1). Запас электромагнитной энергии в контуре с током I, нахо­дящемся в поле постоянного магнита, выражается формулой:

W_М = І·Ψ,

где Ψ— полное потокосцепление данного контура с магнитным полем постоянного магнита. Тогда

М_ВР = Ι·dΨ / dα. (2.3)

При повороте рамки на угол dα каждая ее сторона опишет дугу dα·b/2, пересекая при этом силовые линии магнитного поля; число пересеченных линий будет равно произведению пройденного пути dα·b/2 на длину активной стороны рамки l и на индук­цию в зазоре В.

Полное изменение потокосцепления с рамкой равно произве­дению числа силовых линий, пересеченных обеими сторонами рамки, на число витков ее обмотки, т. е.

dΨ = 2·Βlω dα·b/2,

где ω - число витков обмотки.

Произведение·Βl равно площади рамки; обозначив ее через S, получим:

dΨ =BSωdα.

Если положить dα =1 рад, то произведение BSω - величина постоянная для каждого данного прибора - будет равна измене­нию потокосцепления при повороте рамки на 1 рад. Обозначая его через Ψ₀, запишем:

Ψ₀ = BSω [вб/рад], (2.4)

Тогда

dΨ = Ψ₀ · dα. (2.5)

Подставляя выражение (2.5) формулу (2.3), получим вы­ражение вращающего момента для магнитоэлектрического меха­низма в следующем виде:

М_ВР = Ι · Ψ₀. (2.6)

Установившееся положение подвижной катушки наступает при равенстве вращающего и противодействующего моментов М_ВР = М_ПР, т.е. с учетом (2.2) запишем:

Ι ·Ψ₀ = W·α. (2.7)

Отсюда находим уравнение шкалы измерительного механизма магнитоэлектрической системы

α = Ι · Ψ₀ / W

или

α = S · Ι, (2.8)

где величина S = Ψ₀ / W является чувствительностью прибора (в радианах на ампер).

Используя выражение (2.4) можно ввести в уравнение шкалы конструктивные параметры измерительного механизма:

α = Bsω Ι · 1/W, (2.9)

т.е. угол отклонения подвижной части прямо пропорционален току в рамке, поэтому магнитоэлектрические приборы имеют равномерные шкалы.

Успокоение подвижной части магнитоэлектрических приборов магнитоиндукционное, т.е. создается взаимодействием магнитных полей от вихревых токов в каркасе рамки и поля постоянного магнита.

Достоинства: высокий класс точности, равномерная шкала, высокая и стабильная чувствительность, малое собственное потребление мощности, большой диапазон измерений, на показания МЭП не влияют внешние магнитные и электрические поля.

Недостатки: без преобразователей МЭП используют только в цепях постоянного тока, имеют малую нагрузочную способность, сложны и дороги, на их показания влияют колебания температуры.

Метрологические характеристики MЭП: классы точности – 0,05; 0,1 и т.д., равно-мерная шкала, высокая и стабильная чувствительность, малое собственное потребление мощности, большой диапазон измерений, большой МВР, успокоение только магнитоиндукционное.

Применение: Магнитоэлектрические измерительные механизмы используют в амперметрах, вольтметрах, гальванометрах (обычных, баллистических и вибрационных) и омметрах.

МЭП используют для измерения постоянного тока – I, напряжения – U, сопротивления – R.

Рис. 2.3. Магнитоэлектрические измерительные приборы серии PQ

Магнитоэлектрические приборы могут быть использованы и для измерения переменного тока и напряжения, но с преобразователями переменного тока в постоянный. Это выпрямительные, термоэлектрические и электронные приборы. Обычно такие приборы градуируются в действующих значениях тока или напряжения.

На рис. 2.3. представлены магнитоэлектрические измерительные приборы серии PQ, которые используются для измерения постоянного тока или напряжения; диапазон измерений от 100mА до 100А, от 15mV до 600V ; сменные шкалы; работа с шунтами; монтаж на щите; габаритные размеры: 48 х 48, 72 х 72, 96 х 96, 144 x 144. Класс точности 1,5;

Измерение постоянного тока и напряжения

Такие измерения производят в основном с помощью магнитоэлектрических амперметров и вольтметров.

Измерительный механизм магнитоэлектрических амперметров и вольтметров принципиально не различаются, а в зависимости от назначения прибора меняется его измерительная цепь. В амперметрах измерительный механизм непосредственно или с помощью шунта включается в цепь последовательно с нагрузкой. В вольтметрах последовательно с измерительным механизмом включается добавочный резистор, и прибор подключается к тем точкам схемы, между которыми необходимо измерить напряжение.

Прямое измерение малых токов и напряжений осуществляется с помощью гальванометра магнитоэлектрической системы. Они представляют собой прибор высокой чувствительности по току и напряжению с неградуированной шкалой. Преимущественное применение гальванометры получили при нулевых методах измерения в качестве приборов, позволяющих с большой точностью фиксировать отсутствие тока в цепи. Гальванометры после соответствующей градуировки могут быть использованы для измерений весьма малых токов и напряжений и для измерения количества электричества.

Существует много различных видов гальванометров, но массовое распространение получили две модификации: гальванометры с подвижной рамкой; гальванометры с подвижным магнитом, к которым относится так называемый вибрационный гальванометр.

Гальванометры постоянного тока. На рис. 2.4 показано устройство магнитоэлектрического гальванометра постоянного тока. Сильный постоянный магнит 1 из высококоэрцетивного сплава, полюсные наконечники 2 из магнитомягкой стали с цилиндрической расточкой концов, неподвижный стальной цилиндр 3, укрепленный в расточке, служат для создания в зазоре сильного равномерного магнитного поля. В этом зазоре находится рамка 4,укрепленная на подвесе 5; ток подводится через безмоментные спирали 6. На оси рамки закреплено зеркальце 7 для оптического отсчета угла отклонения рамки от нулевого положения.

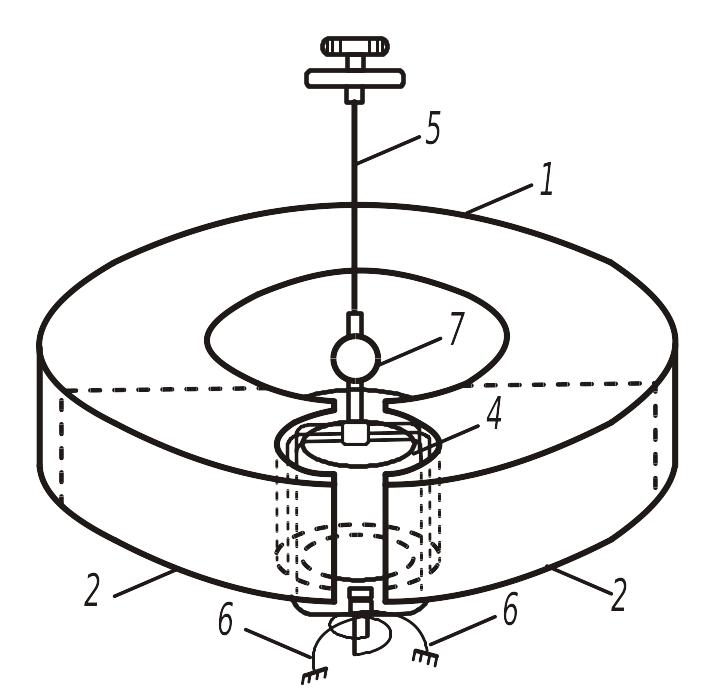
Рис. 2.4. Устройство магнитоэлектрического гальванометра.

На рамку, при подаче тока I действуют моменты: вращающий М_ВР (2.6), успокоения М_У = − Р dα/dt, направленный в сторону, противоположную М_ВР. и противодействующий момент, создаваемый при закручивании подвеса М_ПР = Wα.

Величина P = Ψ₀ / (R_Г + R_ВН) называется коэффициентом успокоения и определяется конструктивными параметрами гальванометра Ψ_0, R_Г и сопротивлением внешней цепи R_ВН. Изменяя R_ВН можно изменять коэффициент успокоения.

И звестно, что движение вращающегося тела определяется уравнением

где J – момент инерции тела; d²α/dt² – угловое ускорение; ΣM – сумма вращающих моментов, действующих на тело.

Для гальванометра это уравнение имеет вид:

(2.10)

Подставляя в уравнение (2.10) значения моментов с учетом их знака получим дифференциальное уравнение движения подвижной рамки гальванометра:

Интеграл этого дифференциального уравнения второго порядка с постоянными коэффициентами и с правой частью, как известно состоит из двух членов: α_С –частного решения при заданных условиях и α₀ – общего решения данного уравнения без правой части, т.е.

α = α_С + α₀ (2.11)

Частное решение уравнения (2.11), рассмотренное для случая установившегося равновесия подвижной части гальванометра, когда скорость ее движения (dα/dt ) и ускорение (d²α/dt²) будут равны нулю, через выражение (2.7) получим

α_с = S₁  I (2.12)

Уравнение (2.11) без правой части для получения общего решения имеет вид:

(2.13)

Решением его будет функция

(2.14)

Где С₁ и С₂ постоянные интегрирования, получаемые из начальных условий; Х₁ и Х₂ – корни характеристического уравнения

JX² + PX + W = 0 (2.15)

Нахождение этих корней и подстановка их в выражение (2.13) и далее полученного значения α₀ в (2.11) дает искомое аравнение движения подвижной части гальванометра:

α = F(t) (2.16)

График функции (2.16) для различных значений сопротивления нагрузки приведен на рис.2.5.

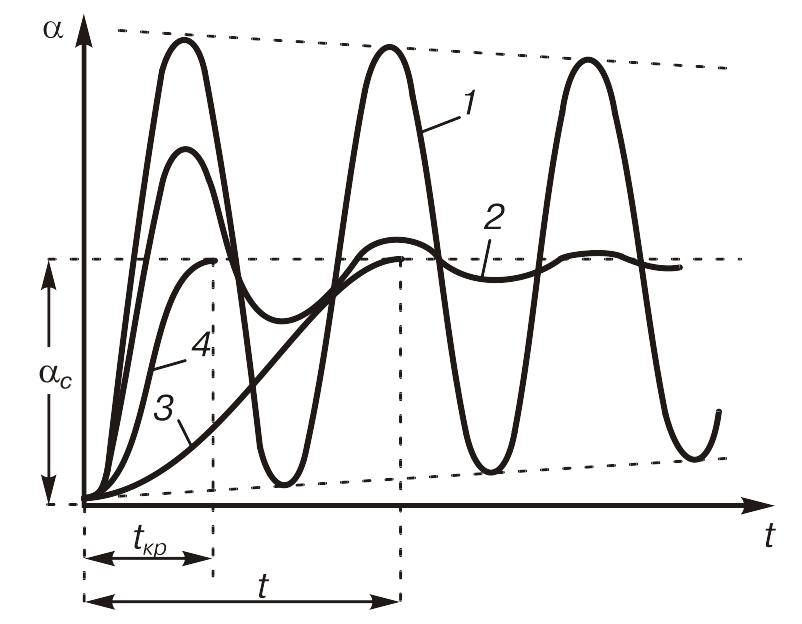
Рис.2.5. Режимы движения подвижной части гальванометра.

При R_ВН = ∞ колебания подвижной части гальванометра будут постепенно, хотя и медленно, затухать из-за трения подвижной рамки о воздух ( кривая 1) и режим движения рамки - колебательный.

При R_КР < R_ВН < ∞ подвижная часть совершает затухающие колебательные дви­жени­я около положения установившегося равновесия, определяемого углом αс (кривая 2)

При R_ВН < R_КР режим движения рамки гальванометра будет апериодическим (кривая 3).

При Rвн = Rкр подвижная часть приходит в режим устойчивого равновесия без колебаний и за минимальное время (кривая 4). Этот режим называется критический.

Значение критического сопротивления Rкр предопределяет возможность приме­нения гальванометра и его всегда указывают на шкале прибора.

Метрологические характеристики: чувствительность, период собственных колебаний, внешнее и полное критическое сопротивление.

Измерение сопротивления

Для измерения больших сопротивлений используются магнитоэлектрические омметры или омметры-логометры.

Логометры – приборы электромеханической группы, измеряющие отношение двух электрических величин α = ƒ (Х₁/Х₂). В логометрах вращающий и противодействующий моменты создаются электрическим путем и направлены навстречу друг другу. Логометры используются для измерения электрических величин, например сопротивления, емкости, частоты, угла сдвига фаз и др. Они широко применяются при измерении неэлектрических величин электрическими методами, например в расходомерах, измерителях уровня и др.

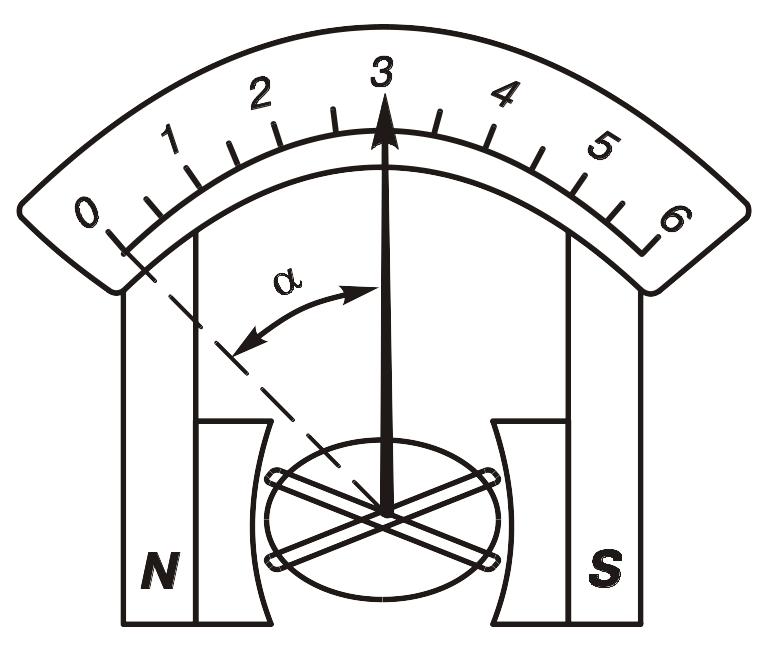
Рис. 2.6. Устройство магнитоэлектрического логометра

Устройство. На рис. 2.6 приведена схема устройства магнитоэлектрического логометра.

В поле постоянного магнита помещена подвижная часть, состоящая из двух жестко закрепленных под определенным углом рамок. Особой формой полюсных наконечников и сердечника, находящегося между ними, искусственно создается неравномерное магнитное поле постоянного магнита. Токи к рамкам подводятся через безмоментные спирали, не создающие противодействующего момента.

Направление тока в рамках логометра выбираются так, чтобы вращающие моменты М₁ и М₂ были направлены в разные стороны. Тогда в общем виде можно записать:

М₁ = I₁ · ƒ₁ (α); М₂ = I₂ · ƒ₂ (α), (2.17)

где I₁ и I₂ - токи в рамках; α – угол отклонения подвижной части от некоторого условного нулевого положения.

Равновесие подвижной части наступает при равенстве моментов М₁ и М₂, действующих на рамку т.е. при условии:

I₁·ƒ₁ (α) = I₂ ·ƒ₂ (α),

Откуда

I₁ / I₂ = ƒ₂ (α)/ ƒ₁ (α) = ƒ (α)

или

α = F (I₁/ I₂). (2.18)

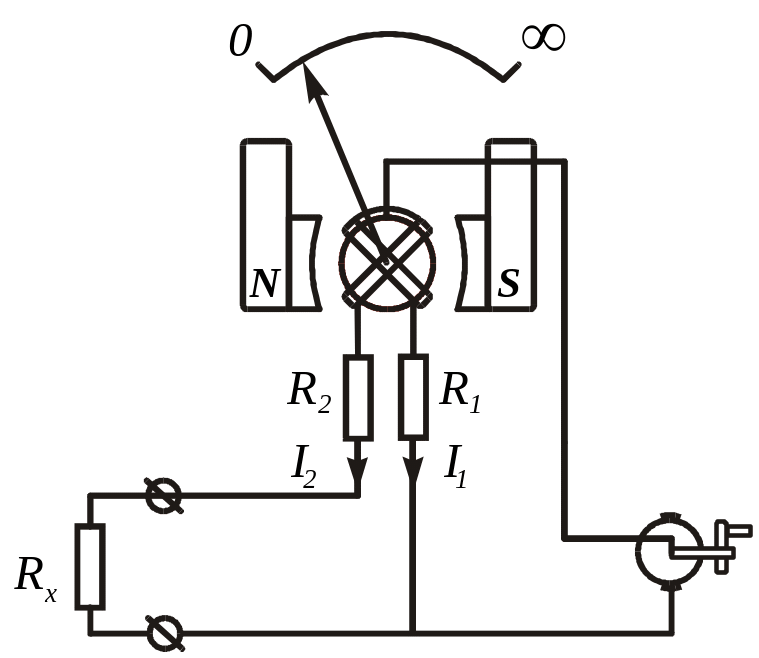
Рис.2.7. Устройство магнитоэлектрического омметра.

Для данного случая I₁ = U/(R₁ + r₁); I₂ = U/(R₂ + r₂ + R_X),

Где U – напряжение генератора; r₁ и r₂ - сопротивления обмоток рамок.

Тогда согласно выражению (2.18) уравнение шкалы прибора запишется:

α = F [(R₂ + r₂ + R_X)/(R₁ + r₁)]; (2.19)

Шкала прибора градуируется в Ом.

Аналогично рассмотренному принципу построения логометрического ИМ магнитоэлектрической системы выпускают логометры электромагнитной, электродинамической, ферродинамической и индукционной систем.

Основное достоинство логометрических приборов является независимость их показаний от напряжения питания.