Коррекция сар.

Если в результате компьютерного моделирования установлено, что САР оказалась неустойчивой или ее показатели качества не соответствуют заданным, то дальнейший процесс моделирования сводится к выбору корректирующих элементов в соответствии с рекомендациями, изложенными далее.

Под коррекцией САР понимают изменение ее структурных схем с целью обеспечения устойчивых с требуемыми показателями качества переходных процессов. Коррекция САР достигается посредством введения в систему дополнительных, так называемых корректирующих элементов (устройств), охватывающих один или несколько элементов исходной системы. Если направление сигналов (воздействий) в корректирующем устройстве совпадает с направлением сигналов в охватываемых им элементах, то связь называют прямой. В противном случае связь будет обратной. Коррекцию САР на основе прямых связей принято называть последовательной, а с использованием обратных связей — параллельной.

Рассмотрим случаи последовательной коррекции САР.

Пусть задана структурная схема САР (рис. 7), в которую введен дополнительный корректирующий элемент с передаточной функцией W_K(p), обеспечивающий прямую положительную связь.

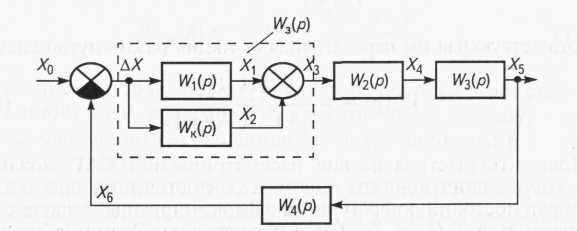
Рис. 7. Структурная схема САР с последовательной коррекцией

Зачастую при создании САР на первом этапе проектирования в алгоритм ее функционирования закладывают простейший закон регулирования, согласно которому связь между сигналом рассогласования ΔХ и сигналом Х₁ следующая:

где k₁ — передаточный коэффициент.

Такой закон регулирования называют пропорциональным (П-закон регулирования). Ему соответствует передаточная функция

В качестве корректирующего элемента (см. рис. 7) может быть принято идеальное дифференцирующее звено с передаточной функцией

где Т_Д — постоянная времени.

С учетом этих выражений закон регулирования примет вид

Соответствующая ему эквивалентная передаточная функция

Закон регулирования X₃ с введением производной называется пропорционально-дифференциальным (ПД-законом регулирования). Регулятор, реализующий ПД-закон регулирования, реагирует не только на значение отклонения регулируемой величины в данный момент времени, но и на скорость изменения отклонения. Следовательно, регулятор работает с опережением, улучшая качество переходного процесса за счет учета тенденции последующего его развития, т. е. увеличивает быстродействие системы и запас устойчивости.

Эффективность введения в закон регулирования первой производной от сигнала рассогласования проиллюстрируем на следующем примере.

а соответствующая им передаточная функция разомкнутой системы

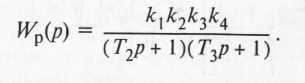
Пусть передаточные функции исходной САР (см. рис. 7) имеют следующий вид: -|

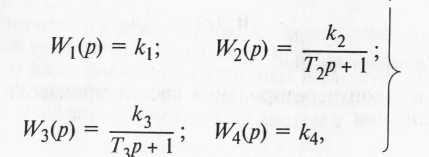
Повысить быстродействие рассматриваемой САР можно за счет уменьшения влияния, например, постоянной времени Т₂, подобрав постоянную времени дифференцирующего звена с учетом равенства T_Д/k₁ = Т₂. Тогда передаточная функция скорректированной разомкнутой САР

Из этого выражения видно, что введение в закон регулирования производной обеспечивает полную компенсацию влияния постоянной времени Т₂ и, следовательно, улучшает динамические свойства системы.

В качестве корректирующего элемента (см. рис. 7) можно использовать идеальное интегрирующее звено с передаточной функцией

где Т_и — постоянная времени.

Тогда в закон регулирования вводят интеграл от сигнала рассогласования

Соответствующая ему передаточная функция

В этом случае закон регулирования, называемый пропорционально-интегральным (ПИ-законом регулирования), будет описываться следующим уравнением:

Введение интеграла в закон регулирования исключает статическую ошибку САР, превращая ее в астатическую систему, но при этом одновременно уменьшаются запас устойчивости и быстродействие системы.

В качестве корректирующих элементов можно одновременно применять дифференцирующие и интегрирующие звенья. В данном случае получается ПИД-закон регулирования, реализующий алгоритм

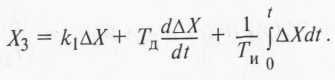
Сегментное введение производной и интеграла обеспечивает желаемое быстродействие, необходимый запас устойчивости и от­сутствие статической ошибки САР.

Для последовательной коррекции статических САР можно использовать интегрирующее звено, последовательно включенное в канал прямой связи САР. В таком случае статическая САР превращается в астатическую, у которой отсутствует статическая ошибка. В результате такого включения интегрирующего звена получается интегральный закон (И-закон) регулирования:

где X_{вых ,}X_вх— соответственно выходная и входная величина звена ,

Для этого закона регулирования передаточная функция

Обобщая изложенное и учитывая результаты анализа различных законов регулирования, можно сформулировать следующие рекомендации по их использованию.

П-закон регулирования рекомендуется для объектов с небольшим запаздыванием и незначительными изменениями внешних возмущений. Обычно его применяют в САР, содержащих одно-и двухъемкостные объекты регулирования.

И-закон регулирования целесообразно применять в тех случаях, когда допускается большое время регулирования. Его нельзя использовать на объектах без самовыравнивания и с большим запаздыванием так как процесс регулирования может быть неустойчивым. Если И-закон регулирования должен обеспечивать работу, САР при непрерывно изменяющемся внешнем воздействии, то необходимо, чтобы максимальная скорость изменения регули­рующего воздействия превышала скорость изменения внешнего

ПИ-закон регулирования обеспечивает работоспособность САР практически при сколь угодно широком диапазоне изменения внешних возмущений.

ПД-закон регулирования можно использовать в системах с большим временем запаздывания.

ПИД закон регулирования пригоден для САР с большим временем запаздывания, значительными и резкими изменениями внешних воздействий.

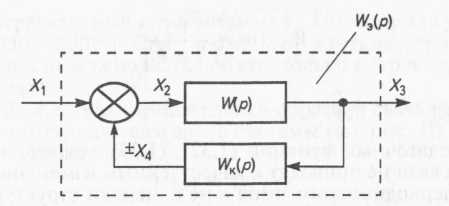
Рис. 8. Структурная схема элемента САР, охваченного обратной связью

Параллельная коррекция САР, как отмечено ранее, обеспечивается посредством обратных связей. Обратные связи могут быть положительные или отрицательные, жесткие или гибкие (рис. 8).

Жесткая обратная связь формируется, если передаточная функция корректирующего элемента W_K(p) = k_к, т. е. если в качестве корректирующего элемента использовано безынерционное (пропорциональное) звено. Если в качестве корректирующего элемента применяют идеальное дифференцирующее звено с передаточной функцией W_K(p) = Tp, то получают гибкую обратную связь, которая действует только в переходном режиме работы САР.

Эффективность и область применения различных вариантов обратных связей для коррекции САР можно уяснить на следующих примерах.

Пример 1. Жесткой обратной связью с передаточной функцией W_K(p) = k_K охвачено апериодическое звено (см. рис. 8), имеющее передаточную функцию

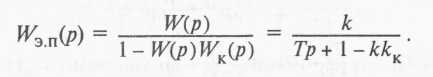
При положительной обратной связи эквивалентная передаточная функция

Разделив знаменатель и числитель этого выражения на 1 — kk_K, получим

Для отрицательной обратной связи

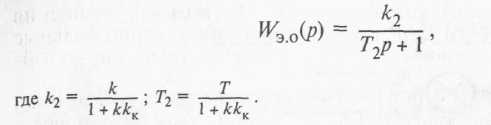
Из передаточных функций следует, что жесткие обратные связи не приводят к качественным изменениям охватываемого апериодического звена и не изменяют структурную схему системы, но изменяют постоянную времени и передаточный коэффициент апериодического звена.

Положительная жесткая обратная связь увеличивает постоянную времени Т₁ и коэффициент k₁ эквивалентного апериодического звена. Следовательно, она уменьшает быстродействие и запас устойчивости системы. Если в выражении kk₁ > 1, то обратная связь превращает устойчивое апериодическое звено в неустойчивое.

Отрицательная жесткая обратная связь уменьшает постоянную времени T₁ и передаточный коэффициент k₁ эквивалентного апе­риодического звена. Следовательно, она увеличивает быстродействие, устойчивость и статическую ошибку системы.

Охват апериодического звена жесткими обратными связями можно применять для коррекции только структурно-устойчивых САР.

Пример 2. Жесткой обратной связью охвачено колебательное звено системы (см. рис. 8). Передаточные функции

Выполнив те же преобразования, что и в предыдущем примере, получим

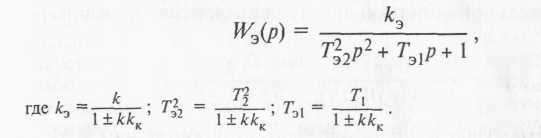
Знак «плюс» в знаменателях постоянных времени и коэффициента передачи относится к отрицательной обратной связи, а «минус» — к положительной.

Эквивалентная передаточная функция W_э(p) не отличается от исходной передаточной функции W(p). Следовательно, введение жесткой обратной связи вокруг колебательного звена не изменяет структурной схемы САР.

Из выражения видно, что отрицательная обратная связь уменьшает, а положительная увеличивает постоянные времени Т_э2, Т_э1 и передаточный коэффициент k_э. Поэтому для улучшения динамических свойств САР применяют жесткие отрицательные связи. Причем их можно использовать только в структурно-устойчивых системах.

Пример 3. Жесткая отрицательная обратная связь [ W_K(p) = k_K] охватывает интегрирующее звено системы (см. рис. 8), передаточная функция которого

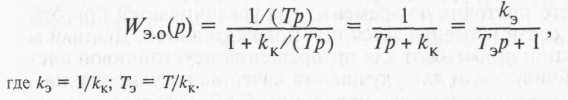
Из передаточной функции следует, что при охвате интегрирующего звена жесткой отрицательной обратной связью эквивалентная передаточная функция будет соответствовать апериодическому звену, т. е. структурная схема САР изменится.

Этот метод коррекции можно применять для улучшения динамических свойств (устойчивости и качества регулирования) и для превращения структурно-неустойчивых систем в структурно-устойчивые или астатических систем в статические.

Пример 4. Гибкая обратная связи [ W_K(p) = Т_др] охватывает апериодическое звено с передаточной функцией (см. рис. 8).

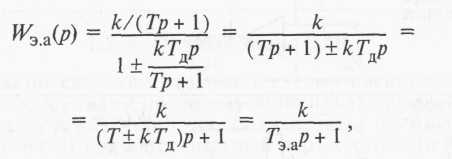
- постоянная времени эквивалентного звена (знак «плюс» для

отрицательной связи, «минус» для положительной).

Эквивалентная передаточная функция

Анализ передаточной функции показывает, что гибкая отрицательная обратная связь увеличивает постоянную времени Т_{э а}, а гибкая положительная уменьшает ее. При этом коэффициент передачи к не изменяется.

При введении гибкой отрицательной связи вокруг апериодического звена повышаются устойчивость и качество переходного процесса (вместо затухающего колебательного можно получить монотонный переходный процесс), но при этом снижается быст­родействие системы.

Пример 5. Гибкая обратная связь

введена вокруг интегрирующего звена с передаточной функцией

(см. рис. 8). В данном случае эквивалентная передаточная функция (рис. 8). В данном случае эквивалентная передаточная функция

Из передаточной функции видно, что гибкая обратная связь не изменяет структурную схему интегрирующего звена, но изменяет его постоянную времени: она увеличивается при отрицательной связи и уменьшается при положительной. Данный метод коррекции применяют для превращения неустойчивой системы в устойчивую или для улучшения качества регулирования.

В рассмотренных методах коррекции САР использованы идеальные дифференцирующие и интегрирующие звенья, которые реализовать на практике простыми средствами очень сложно. Поэтому для коррекции автоматических систем часто используют более простые, так называемые реальные дифференцирующие и интегрирующие звенья.

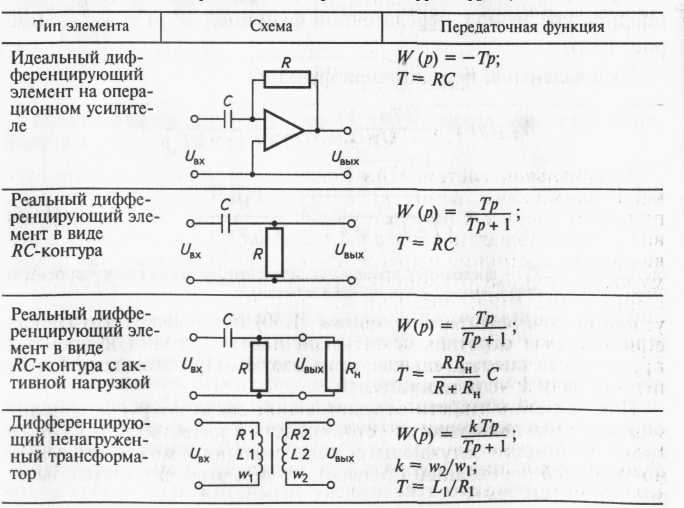
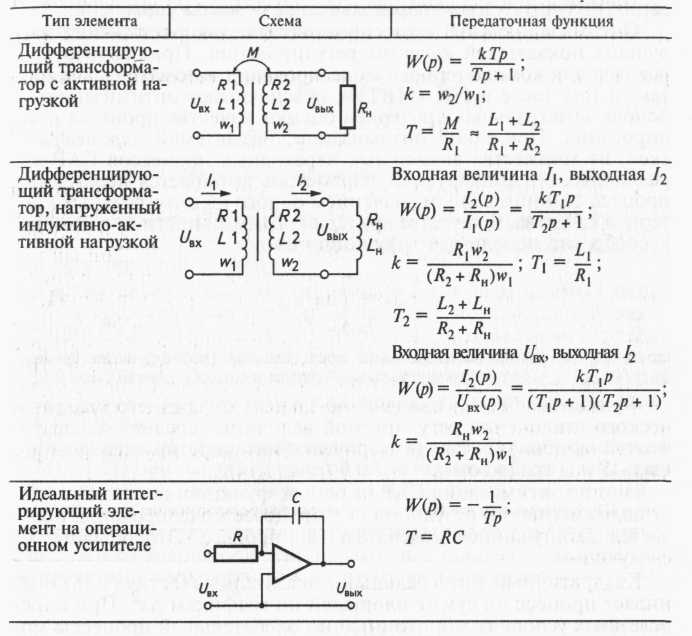
Схемы и передаточные функции некоторых идеальных и реальных корректирующих элементов показаны в таблице 1.

Таблица 1. Идеальные и реальные электрические корректирующие элементы