1.

Основные понятия. СВ.

Случайная величина

2.

Основные теоремы . Сумма и произведение событий. Теоремы сложения и умножения вероятностей.

3.

Формула полной вероятности. Теорема гипотез (формула Байеса).

4.

СВ и их законы распределения. Ряд распределения. Функция распределения. (ряд распределения)

5.

Плотность вероятности и ее свойства.

6.Характеристическая функция и ее свойства. Это один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Характеристической функцией случайной величины X называется функция , где i - мнимая единица. Функция g(t) представляет собой математическое ожидание некоторой комплексной случайной величины , функционально связанной с величиной X. При решении многих задач теории вероятностей оказывается удобнее пользоваться характеристическими функциями, чем законами распределения. Зная закон распределения случайной величины X, легко найти ее характеристическую функцию. Если X - прерывная случайная величина с рядом распределения

то её характер-ая функция будет . Если X  неприр-ая случайная величина с плотностью распределения  f(x), то ее характеристическая функция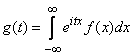 .  Свойства: 1)Характеристическая функция однозначно определяет распределение. Пусть X,Y суть две случайные величины, и  . Тогда  . В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности; 2) Характеристическая функция всегда ограничена: .; 3) Характеристическая функция в нуле равна единице: .; 4) Характеристическая функция всегда непрерывна:  .; 5) Характеристическая функция как функция случайной величины однородна: .; 6) Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Пусть   суть независимые случайные величины. Обозначим  . Тогда

7.

Числовые характеристики СВ. Математическое ожидание и дисперсия СВ.

Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её мат.ожидания: для прерывных D[X]=M[(X-mx)^2] ; для непрерывных D[X]=ƒ((x-m(x))^2)f(x)dx.

8.

Основные модели плотности вероятности, используемые в статистической радиотехнике.

9.Определение законов распределения св на основе опытных данных. Гистограмма. Критерии согласия, 2-Пирсона, Колмогорова.

10.Системы СВ. Ф-ии распр. сис-мы из двух СВ. Двумерн пл-ь вер-ти. Свойство: неотрицательна.

11.

Условные законы распределения отдельных СВ, входящих в систему СВ. Статистическая взаимозависимость и независимость.

12.

Числовые характеристики системы двух СВ. Коррелированность.

13.Числовые характеристики системы из нескольких св. Двумерный нормальный закон плотности вероятности.

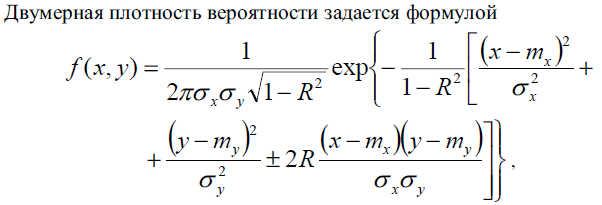
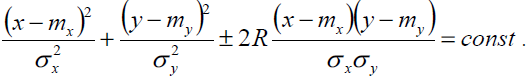
19.

Огибающая и фаза узкополосного СП.

22.

Действие белого шума на RC-фильтр нижних частот.

Стационарный шум — шум, который характеризуется постоянством средних параметров: интенсивности (мощности), распределения интенсивности по спектру (спектральная плотность), автокорреляционной функции.

Белый шум — стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот. Примерами белого шума являются шум близкого водопада, или шум Шоттки на клеммах большого сопротивления.

В природе и технике «чисто» белый шум (то есть белый шум, имеющий одинаковую спектральную мощность на всех частотах) не встречается (ввиду того, что такой сигнал имел бы бесконечную мощность), однако под категорию белых шумов попадают любые шумы, спектральная плотность которых одинакова (или слабо отличается) в рассматриваемом диапазоне частот.

23.

Действие белого шума на колебательный контур.

Стационарный шум — шум, который характеризуется постоянством средних параметров: интенсивности (мощности), распределения интенсивности по спектру (спектральная плотность), автокорреляционной функции.

Белый шум — стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот. Примерами белого шума являются шум близкого водопада, или шум Шоттки на клеммах большого сопротивления.

В природе и технике «чисто» белый шум (то есть белый шум, имеющий одинаковую спектральную мощность на всех частотах) не встречается (ввиду того, что такой сигнал имел бы бесконечную мощность), однако под категорию белых шумов попадают любые шумы, спектральная плотность которых одинакова (или слабо отличается) в рассматриваемом диапазоне частот.

32. Байесовское решающее правило при простой гипотезе и простой альтернативе.

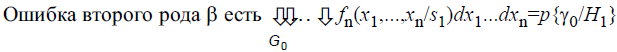
35. Оптимальная оценка амплитуды сигнала.

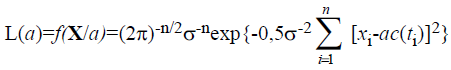
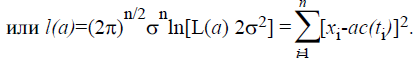
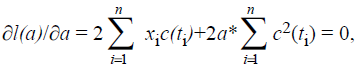
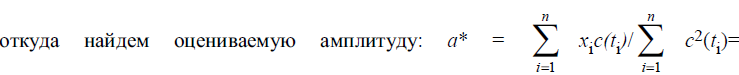
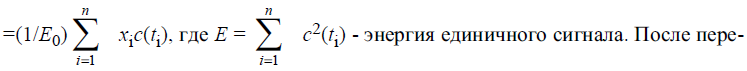
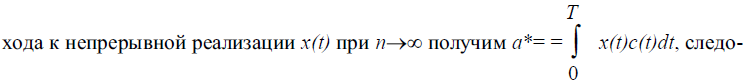
34.

Основы теории оценок. Методы получения оценок (критерии оценок).

14.

СП Общие понятия. Одномерные и многомерные функции распределения и плотности вероятности СП.

Случайный процесс (СП) это некоторый процесс или явление, поведение которого в течение времени и результат заранее предсказывать невозможно. Примеры случайных процессов: динамика изменения курса валют или акций, выручка или прибыль организации с течением времени, объемы продаж товара и т.д. Если случайный процесс может изменить своё состояние только в строго определённый момент времени, то он называется процессом с дискретным временем. Если же смена состояния возможна в произвольный момент времени, то это СП с непрерывным временем. Если в любой момент времени СП представляет собой дискретную случайную величину (ее значение можно перечислить и выделить два соседних значения), то это процесс с дискретным состоянием. Если же в любой момент времени состояние может меняться непрерывно, плавно и нельзя выделить два соседних состояния, то это СП с непрерывным состоянием. Таким образом, возможно 4 вида СП:

1) СП с непрерывным временем и непрерывным состоянием (пример: температура воздуха в некоторый момент времени, изменяется плавно в любой момент времени).

2) СП с непрерывным временем и дискретным состоянием (пример: число посетителей в магазине, изменяется кратно одному в любой момент времени).

3) СП с дискретным временем и непрерывным состоянием (пример: динамика курса курс валюты, изменяется плавно в момент валютных торгов).

4) СП с дискретным временем и дискретным состоянием (пример: число пассажиров в транспорте изменяется кратно одному и только в определенные моменты времени, на остановках).

Рассмотрим некоторую систему S, в которой в данный момент времени t о протекает СП. Этот процесс называется Марковским, если для любого момента времени t > t о , поведение системы в будущем зависит только от того, в каком состоянии система находилась в данный момент времени при t=t о , и никак не зависит от того, как, когда и в каких состояниях она пребывала в прошлом при t<t о . Другими словами, «прошлое»

Марковского процесса никак не влияет на «будущее» (только через «настоящее»). Если существует частная производная функции распределения по x i , то можно определить плотность распределения вероятности. Одномерная плотность распределения вероятностей случайного процесса определяется соотношением

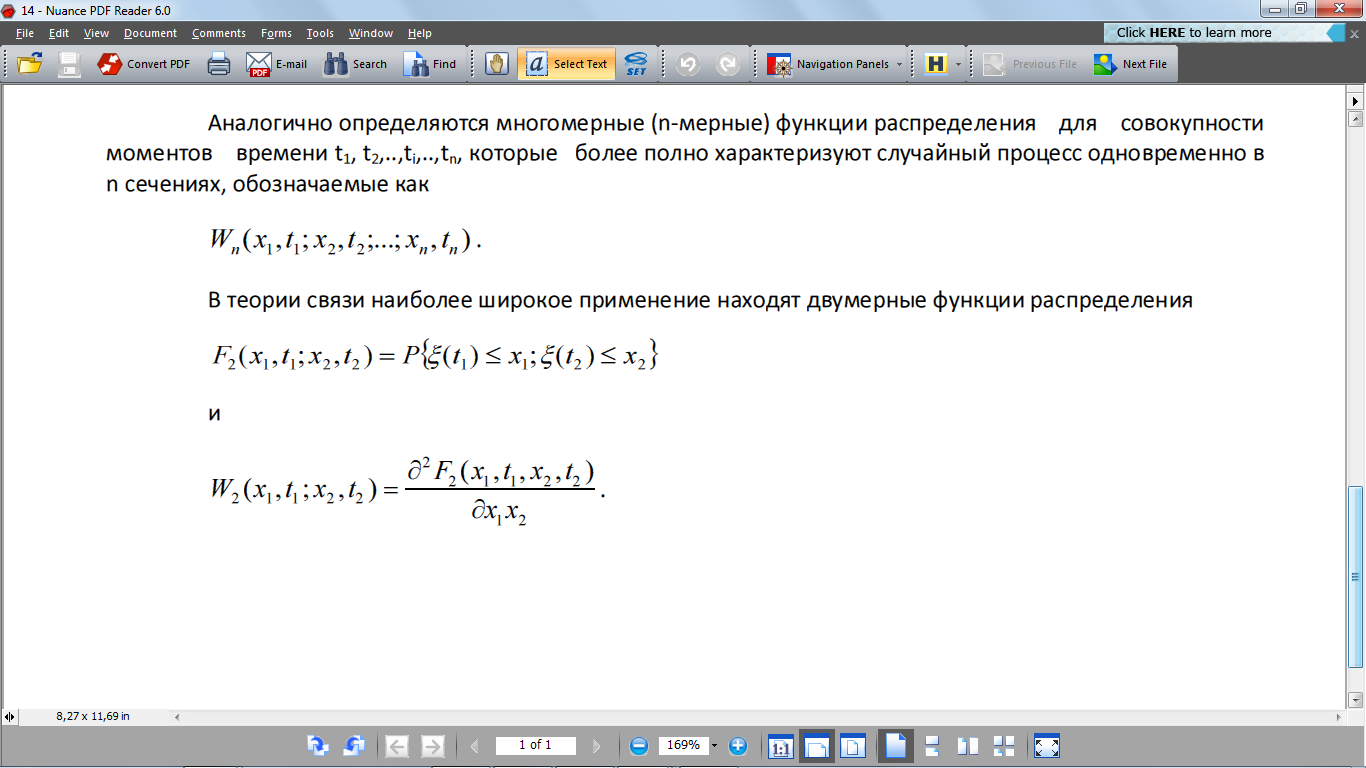
Аналогично определяются многомерные (n-мерные) функции распределения для совокупности моментов времени t ₁ , t ₂ ,..,t _i ,..,t _n , которые более полно характеризуют случайный процесс одновременно в n сечениях, обозначаемые как В теории связи наиболее широкое применение находят двумерные функции распределения

18.

Узкополосные и широкополосные СП. Особенности узкополосных СП.

С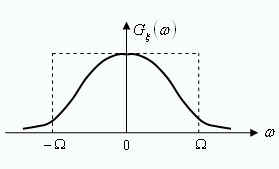 П, для которых определенная в том или ином смысле полоса занимаемых частот много меньше величины |w0|. Такие процессы называются относительно узкополосными, или просто узкополосными. Пусть энергетический спектр процесса сосредоточен в некоторой полосе, включающей нулевую частоту: Такие процессы часто называют низкочастотными, или относительно широкополосными. При этом, определенная в том или ином смысле (см. ниже) ширина полосы занимаемых частот оказывается, как правило, много больше центральной частоты спектра в области положительных (отрицательных) частот.

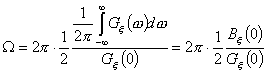-ширина полосы занимаемых частот.

21.

Линейные преобразования СП.

29.

Статистическая теория проверки гипотез.

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки [3, 5, 11]. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.

Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l >10 состоит из бесконечного множества простых гипотез Н0 о равенстве l =bi , где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Принятие или отклонение гипотезы Н0 по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1. Ошибка второго рода возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0. Вероятность отвергнуть ложную гипотезу Н0 называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1.

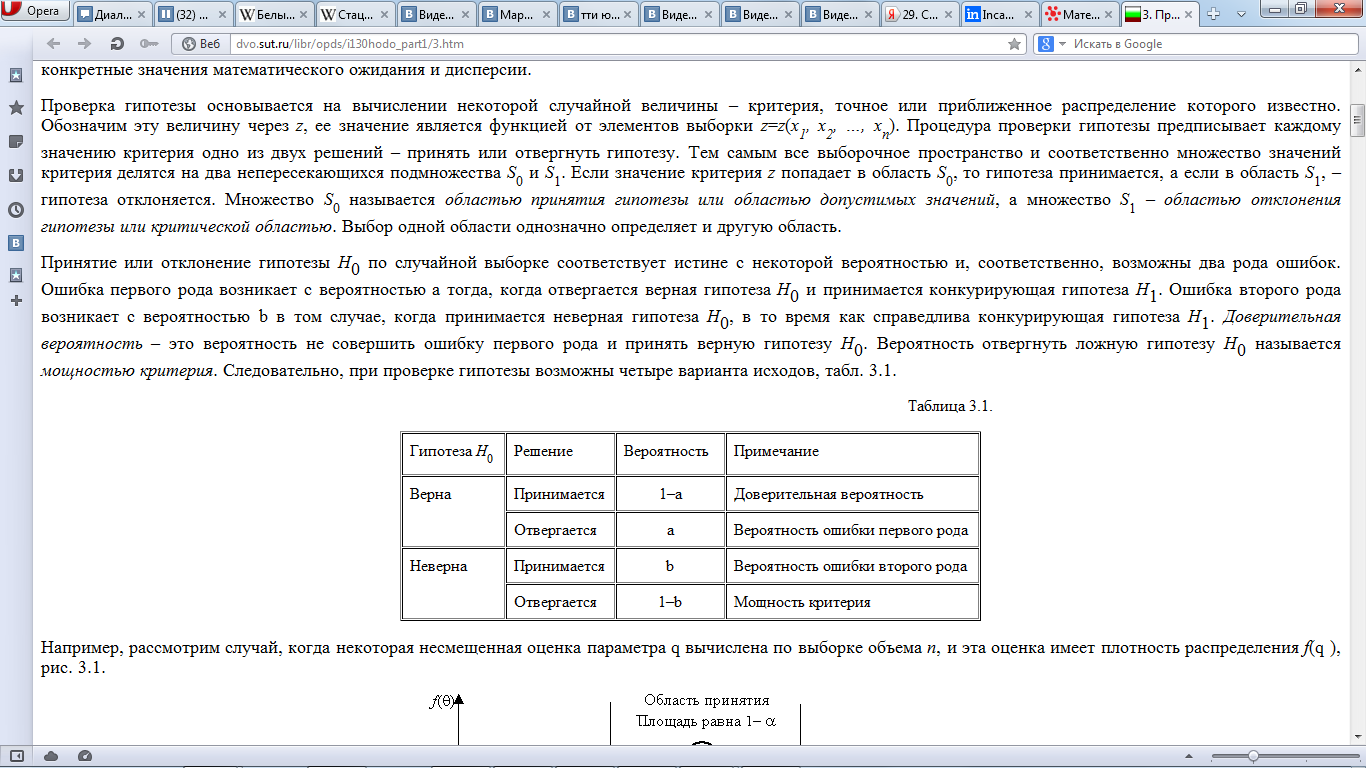При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.

В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.

15.

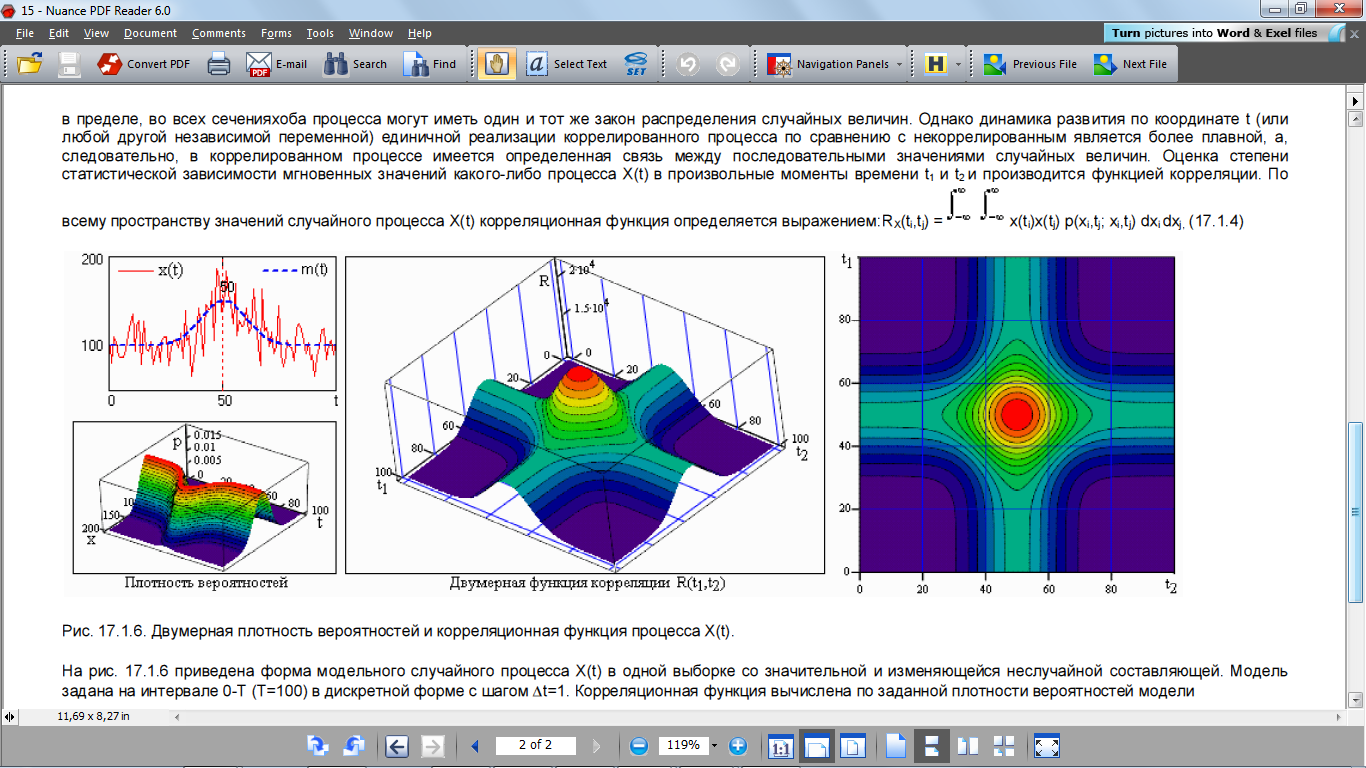
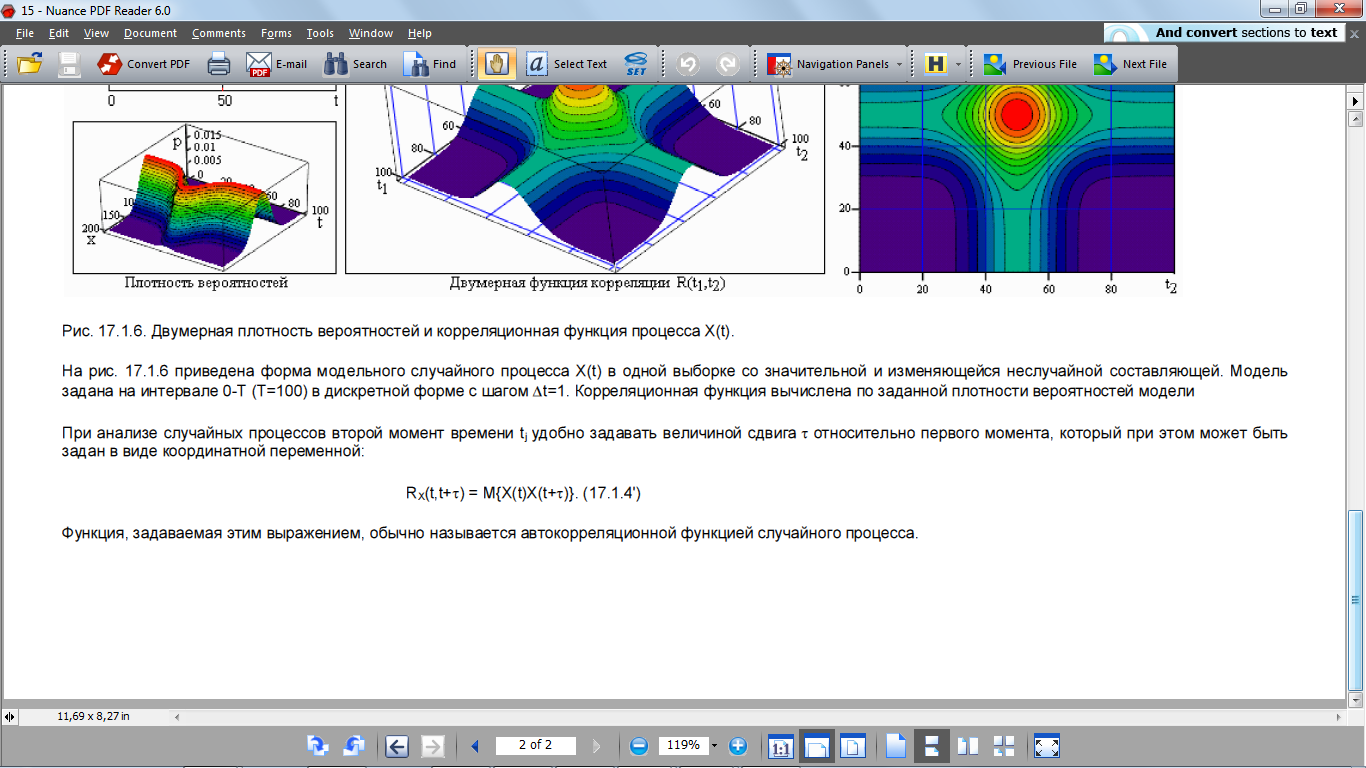
Математическое ожидание и дисперсия СП. Корреляционная функция СП.

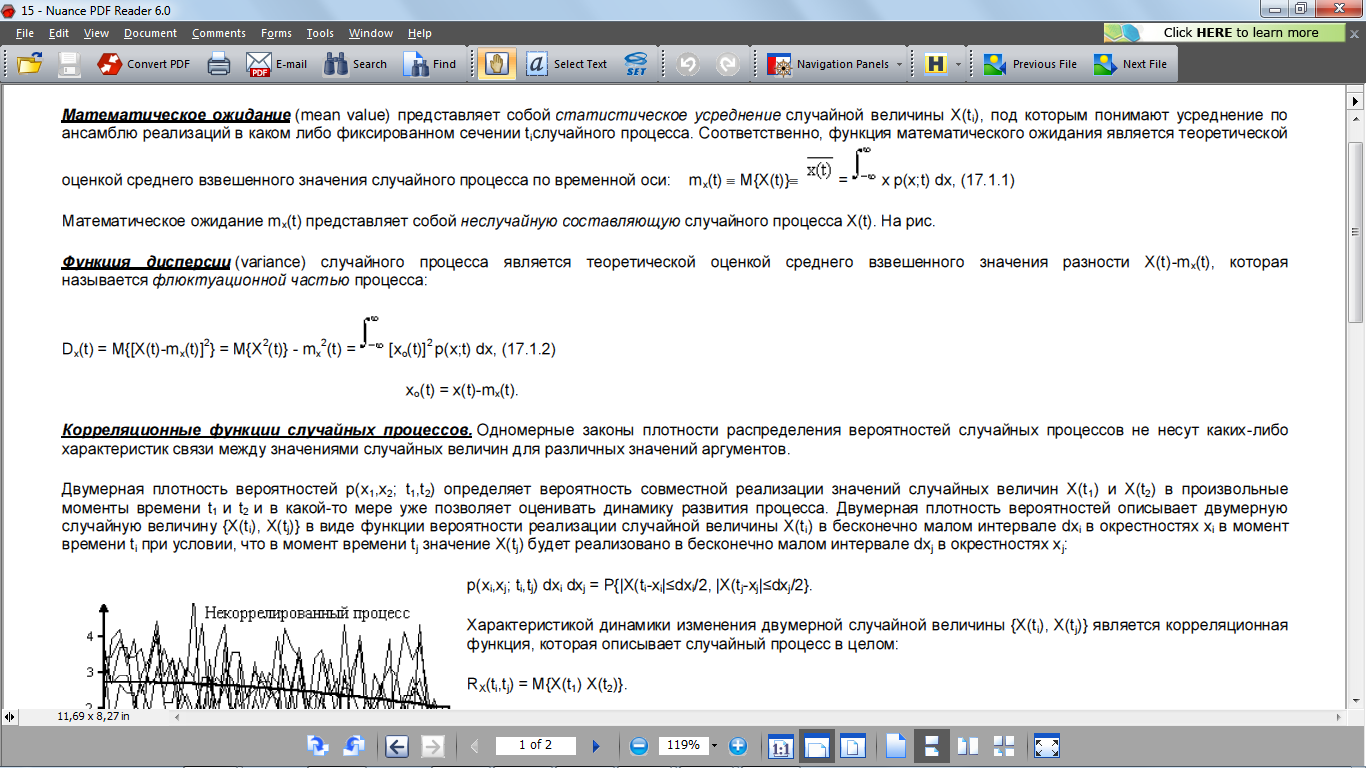
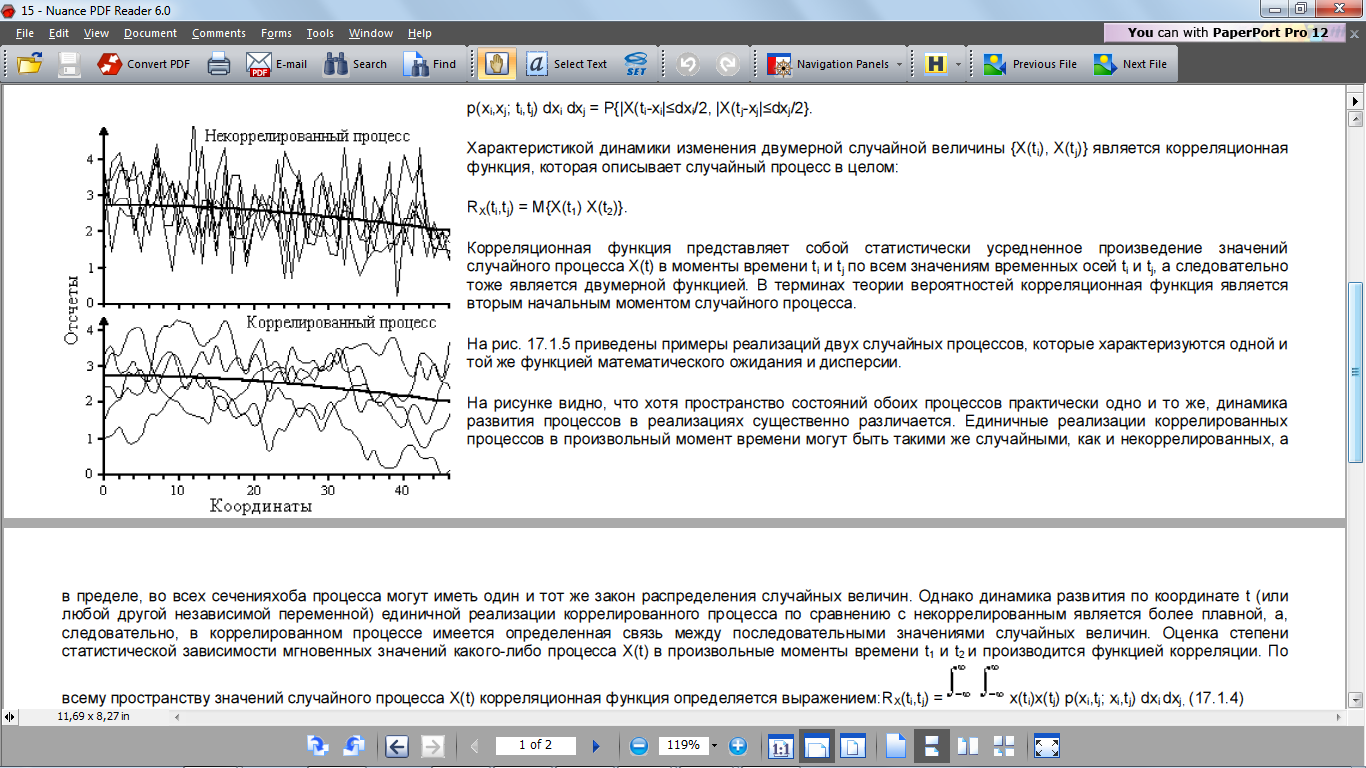
33.Критерий Неймана-Пирсона. Критерий идеального наблюдателя. Минимаксный критерий. Критерий идеального наблюдателя:

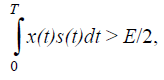
Критерий Неймана-Пирсона: