Оглавление

Краткие теоретические сведения 2

1 Режимы моделирования 2

1.1 Temperature sweep 2

1.2 Worst Case 3

1.3 Monte Carlo 3

2 Резонансные цепи 4

2.1 Добротность резонансной цепи и полоса пропускания 4

2.2 Включение резонансной цепи в транзисторный усилитель 6

3 Лабораторная схема резонансного усилителя 8

4 Расчет резонансного усилителя 9

5 Задание на ЛАБОРАТОРНУЮ РАБОТУ №4 13

контрольные вопросы 14

Список источников, рекомендуемых для изучения 16

Краткие теоретические сведения

В радиотехнических системах распространены резонансные усилители. В данной лабораторной работе рассматривается транзисторный каскад такого усилителя, который строится на основе апериодического усилительного каскада предыдущей лабораторной работы. Также продолжается изучение режимов моделирования САПР EWB.

1Режимы моделирования

1.1Temperature sweep

Режим моделирования «Temperature sweep» осуществляет температурные испытания моделируемой схемы. Диа­логовое окно для установки параметров моделирования особых пояснений не требует, поскольку оно, за исключением температурного диапазона и отсутствия параметров компонента, не отличается от ок­на других режимов.

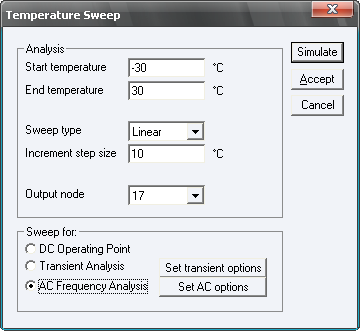
Рис. 11 Окно параметров режима моделирования «Temperature sweep»

1.2Worst Case

Worst Case – расчет режима по постоянному току или частотных характеристик при предельных отклонениях параметров компонентов схемы (расчет на наихудший случай). Отклонение параметров задается для каждого компонента индивидуально в индивидуальном окне параметров компонента. Но можно при этом задать отклонение (tolerance) равным Global, что будет означать глобальное значение отклонения. Это значение устанавливается в окне параметров данного режима (Рис. 11). Collating function – режим расчета схемы (выбираются из предлагаемого списка), при котором: устанавливается максимальное и минимальное значение напряжение в заданном узле (Max. value, Min. Value), максимальная и минимальная частота при одном и том же напряжении (Frequency at max, Frequency at min), максимальное значение частоты пересечения заданного уровня порогового напряжения Threshold снизу-вверх или сверху-вн (Rise edge frequency, Fall edge frequency).

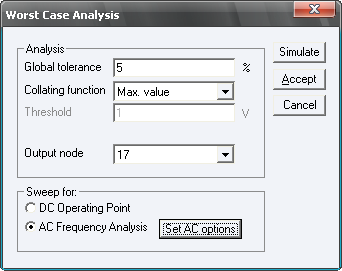
Рис. 11 Окно параметров режима моделирования «Worst Case»

1.3Monte Carlo

Monte Carlo – статистический анализ по методу Монте-Карло. В отличие от расчета на наихудший случай в данном режиме расчеты производятся при случайном значении параметров. Однако, эти значения выбираются в пределах заданного отклонения – tolerance. Закон распределения случайных значений выбирается опцией Distribution type. Uniform — равновероят­ное распределение и Gaussian — гауссовское распределение.

Режим эффективен при большом количестве параметров, когда расчет на наихудший случай дает результаты сложные для анализа.

Рис. 12 Окно параметров режима моделирования «Monte Carlo»

2Резонансные цепи

2.1Добротность резонансной цепи и полоса пропускания

Добротностью резонансного контура называется отношение максимальной энергии, накопленной в течение одного периода, к энергии, рассеиваемой за этот период.

Пиковая энергия, накопленная контуром на резонансной частоте, определяется формулой:

,

(2.1)

rдe – пиковое значение синусоидального тока;

– индуктивность контура.

Энергия рассеиваемая контуром за один период равна:

,

(2.2)

где – сопротивление катушки индуктивности;

– резонансная частота цепи.

Следовательно, добротность контура определяется формулой:

,

(2.3)

Однако, потери в контуре удобнее отображать эквивалентным параллельным включенным сопротивлением . В этом случае, выражение для добротности может быть получено приравниванием импедансов контуров:

,

(2.4)

Из уравнений (3) и (4) видно, что для контура без потерь значение Q стремится к бесконечности ( ).

Ширина полосы пропускания резонансного контура зависит от резонансной частоты и параметра Q:

,

(2.5)

Чем выше значение Q, тем уже полоса пропускания, т.е. тем выше избирательность контура. Избирательность – это способность контура (или усилителя) выбирать заданную полосу частот.

Одиночный колебательный контур имеет большую неравномерность АЧХ в полосе пропускания. Поэтому используют двух- и более контурные резонансные цепи.

Вид частотной характеристики схемы с двумя контурами зависит от коэффициента связи между катушками индуктивности. Коэффициент связи

,

(2.6)

­гдe М ­– взаимная индуктивность двух катушек,

L₁ – ­ индуктивность первичной обмотки,

L₂ – ­ индуктивность вторичной обмотки.

Коэффициент связи количественно описывает степень связи между катушками. Если , то между катушками связь отсутствует. Если , то весь магнитный поток, создаваемый первым контуром, пронизывает обмотку второго контура. На рис. показана частотная характеристика двух связанных контуров при различных значениях .

Критический коэффициент связи:

,

(2.7)

­гдe и ­ добротность соответствующих контуров с учетом их

нагрузки.

Если , то связь между контурами мала (докритическая) и резонансная характеристика двух контуров напоминает характеристику одиночного контура. Если , то связь между контурами очень сильная (сверхкритическая) и частотная характеристика имеет два разнесенных по частоте максимума. Чем сильнее связь, тем дальше расположены максимумы друг от друга и глубже провал между ними. При связь критическая и частотная характеристика максимально "приближается" к прямоугольной, причем полоса пропускания при этом:

,

(2.8)