Лабораторна робота № 3 створення|створіння| і обробка масивів

Мета|ціль|. Отриматитримати практичні навички|навички| створення|створіння| і обробки масивів даних за допомогою мови С++.

Короткі теоретичні відомості

Масив – це тип даних, використовуваний для подання великої кількості даних одного типу. Доступ до елементів масиву організовують за допомогою індексів. Типове оголошення масиву розподіляє пам'ять, що починається з базової адреси. У С++ ім'я масиву – покажчик на базову адресу (фактично константа).

За способом розподілу пам'яті під дані масиви розділяють на статичні й динамічні.

Під час оголошення статичного масиву відбувається|походить| пошук зв'язної області вільної оперативної пам'яті, розмір якої дорівнює числу елементів масиву, помноженому на розмір одного елемента. Кількість байтів, займана |позичати, посідати | одним елементом, визначається його типом.

Мова|язик| С++ допускає масиви будь-якого типу, включаючи масиви масивів (багатовимірні|багатомірні|).

Наприклад. Заданий двовимірний масив дійсних чисел. Визначити математичне очікування|чекання| і дисперсію.

#include <iostream. h>

#include <conio. h>

#define Row 5

#define Col 4

void main ()

{float masRowCol,//оголошення масиву mas, який містить Row*Col //елементів типу float

float m_o = 0, m_o_2=0; int i, j;

for (i = 0; i < Row, i ++)

for (j = 0; j < Col, j ++)

{cin >> masij; //внесення значень елементів

m_o + = masij; //накопичення суми елементів масиву

m_o_2+=masij*masi j;//накопичення суми квадратів елементів масиву

}

m_o = m_o / (Col*Row); //обчислення мат. сподівання/

сout << “\n Математичне сподівання = ” << m_o;

m_o_2 = m_o_2 / (Col*Row); //обчислення моменту другого порядку

cout << “\ n Дисперсія = “ << m_о_2 - m_о*m_0;

getch();

}

Динамічні масиви використовують для гнучкішого розподілу оперативної пам'яті під елементи масиву і керування нею. При цьому в С++ використовують оператори new і delete у вигляді|виді|:

ім’я_массиву = new тип_ елеменау [кількість_елементів] ;

delete [] ім’я_масиву;

при цьому ідентифікатор ім’я_масиву має бути оголошений покажчиком на тип елементів масиву:

тип_елемента * ім’я_масива;

Якщо компілятору не вдається виділити з|із| купи (вільної пам'яті) необхідний обсяг пам'яті, що запрошується оператором new, то ідентифікатору ім’я_масиву привласнюється значення системного покажчика порожнечі|пустоти| NULL.

Під час динамічного розподілу пам'яті під багатовимірні|багатомірні| масиви спочатку за допомогою оператора new відбувається|походить| виділення зв'язної області під ланцюжок покажчиків на рядки масиву (тобто під адреси рядків). Довжина цього ланцюжка визначається кількістю рядків. Далі необхідно ініціалізувати кожний покажчик з|із| ланцюжка адресою, за якою знаходитиметься|перебуватиме| ланцюжок елементів відповідного рядка.

Наприклад. Створити динамічний двовимірний масив чисел, визначити позицію першого нуля у кожному рядку.

#include < iostream. h >

void main()

{ int row, col, i, j, pos;

cout <<  \n уведіть кількість рядків і стовпчиків;

cin >> row>>col;

int ** mas;

mas = new int * row; // розподіл пам’яті під адреси рядків

for (i = 0; i < row; i ++)

{ mas i = new int col; /* розподіл пам’яті під елементи i - того

рядка масиву */

for (j = 0; j < col; j ++)

cin >> mas i j ; // внесення значень елементів масиву

}

for (i = 0; i < row; i ++)

{ pos = -1;

for (j = 0; j < col; j ++)

if (mas ij = = 0) break;

pos = j; /* якщо поточний елемент стовпчика дорівнює

нулю, занести його позицію до змінної pos*/

if (pos <col) cout <<  \ n в  <<i<< - ому рядку нуль знаходиться в 

<<pos<<  стовпчику;

else cout <<  \n  <<i<<  рядок не містить нуля;

}

for(i=0;i<col;i++) delete masi; /*звільнення пам’яті, що була зайнята під елементи i-того рядка */

delete mas; //звільнення пам’яті, що була зайнята під покажчики на рядки.

}

Завдання до лабораторної роботи № 3

1. Вивчити можливості створення та оброблення однотипових даних на прикладі програм, що розглянуто у п.п. «Короткі теоретичні відомості» та «Приклад виконання лабораторної роботи №3». Перевірити роботу наведених програм.

2. Модифікувати програму, яку наведено у п. «Приклад виконання лабораторної роботи №3» таким чином, щоб розподіл памя’ті відбувався динамічно, а не статично. Пояснити принципові відмінності застосованих методів.

3. |задачі|Написати програму, що дозволяє розв’зати поставлену в індивідуальному завданні задачу з використанням масивів. Спосіб зберігання елементів масиву вибрати самостійно. Пояснити вибір.

Приклад виконання лабораторної роботи №3

Приклад використання масивів для збереження та оброблення однотипових даних.

Нехай задано деяку квадратну матрицю розмірності n  n, яка містить дійсні числа. Розіб’ємо дану матрицю на чотири сектори однакового розміру, як показано на рис.1. Будемо вважати, що квадратна матриця є збалансованою,

я

	1 . .	. . n
1 .	1	3
. n	2	4

Рис.1 Сектори

матриці

кщо сума елементів першого та четвертого секторів дорівнює сумі елементів другого та третього секторів. Необхідно написати програму, яка б для будь – якої матриці заданого розміру визначала, чи є така матриця збалансованою.

Для збереження елементів матриці використаємо статичний двовимірний масив даних типу float, а для підрахунку необхідних сум – статичний одномірний масив даних типу float, елементи якого спочатку завжди дорівнюватимуть нулю:

float mas[10][10]; ,//оголошення масиву mas, який містить 100 елементів типу;

float Sum[]={0,0,0,0};//оголошення масиву Sum з чотирма елементами, які //дорівнюють нулю;

int i,j,n;

cin>>n; //ввід кількості елементів масиву

for(i=0;i<n;i++)

for(j=0;j<n;j++)

cin>>mas[i][j]; // внесення значень елементів масиву.

Для визначення суми елементів за секторами необхідно спочатку визначити розмір сектора. Для цього достатньо виконати наступну дію:

int rozmir=n/2;

У даному випадку використане ціле ділення. Тобто, якщо n є числом, яке не кратне 2, змінна rozmir буде цілим числом. Це дозволяє відкинути середній стовпчик і рядок під час визначення розміру сектора, якщо n є числом, яке не кратне 2.

Обчислення суми елементів в секторах можна проводити окремо з кожному сектора, але це збільшить загальний час виконання програми, тому підрахунок сум виконаємо одночасно за один прохід циклу. Наведений нижче фрагмент програми демонструє використання циклів для проходу по всіх елементах масиву і підрахунку всіх чотирьох сум:

for(i=0;i<centr;i++)

for(j=0;j<centr;j++)

{ Sum[0]+=mas[i][j]; //підрахунок суми у першому секторі

Sum[1]+=mas[n-1-i][j]; //підрахунок суми у другому секторі

Sum[2]+=mas[i][n-1-j]; //підрахунок суми у третьому секторі

Sum[3]+=mas[n-1-i][n-1-j]; //підрахунок суми у четвертому секторі

}

Підрахунок суми елементів першого та третього секторів проводить, починаючи з елементів рядка з нульовим індексом у прямому напрямку, другого і четвертого секторів – починаючи з останнього елемента рядка у зворотному напрямку. Аналогічно, накопичення суми елементів першого та другого секторів проводать, починаючи з нульового елемента стовпчика у прямому напрямку, для третього та четвертого секторів – починаючи з останнього елемента стовпчика у зворотному напрямку.

Таким чином, у цілому програма визначення збалансованості заданої матриці матиме вигляд:

#include <iostream.h>

#include <conio.h>

void main()

{ float mas[10][10];

float Sum[]={0,0,0,0};

int i,j,n;

cin>>n;

for(i=0;i<n;i++)

for(j=0;j<n;j++)

cin>>mas[i][j];

int rozmir=n/2;

cout<<"\nc="<<centr+n%2;

for(i=0;i<rozmir;i++)

for(j=0;j<rozmir;j++)

{Sum[0]+=mas[i][j];

Sum[1]+=mas[n-1-i][j];

Sum[2]+=mas[i][n-1-j];

Sum[3]+=mas[n-1-i][n-1-j];

}

for(i=0;i<4;i++)

cout<<"\nSum["<<i<<"]="<<Sum[i];

if ((Sum[0]==Sum[3])&&(Sum[1]==Sum[2])) cout<<"\n збалансована";

else cout<<"\n не збалансована";

getch();}

Зміст|вміст,утримання| звіту щодо лабораторної роботи №3

1. Титульна сторінка |аркуш|: назва дисципліни; номер і найменування роботи; прізвище, ім'я, по батькові студента; дата виконання.

2. Поставлення завдання|задачі|. Слід дати конкретне поставлення, тобто вказати, який масив даних потрібно створити, які під задачі мають розв’язувати.

3. Математична схема розв’язання поставленої задачі

4. Визначення основних змінних і функцій з|із| коментарями.

5. Реалізація функцій.

6. Лістинг основної програми, де має бути вказано, в якому місці та яка функція викликається|спричиняються|.

Варіанти завдань до лабораторної роботи №3

1. Є n міст, зв'язаних мережею шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти найкоротший шлях і його довжину від вказаного міста відправлення до будь-якого іншого відомого міста (метод Форда визначення найкоротшого шляху на графі в інтерпретації Дейкстри). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.

2. Є n міст, зв'язаних мережею шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти довжини найкоротших шляхів між будь-якими двома відомими містами (метод Шимбела визначення найкоротшого шляху на графі ). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.

3. “Життя” – це багатоклітинна істота, яка населяє прямокутну пустелю. Пустеля розбита на осередки, подібні до клітин шахівниці. Осередок|чарунка,вічко,комірка| може бути порожнім|пустим| або вміщати одну клітинку життя. У цьому світі “життя” розвивається за кроками. За один крок в одних осередках клітини гинуть, а в інших- зароджуються. Зміна поколінь “життя” відбувається за такими правилами:

- сусідами клітини називаються клітини, що знаходяться у восьми осередках, дотичних з осередком, що містить клітину;

- якщо клітина має двох або трьох сусідів, то вона зберігає себе на наступному такті “життя”;

- якщо клітина має більше ніж три або менше ніж два сусіди – вона гине. У першому випадку – від перенаселеності, у другому – від “самотності”;

- якщо у клітині немає “життя”, але у неї рівно три сусідні клітини, то у ній зароджується “життя”.

Необхідно написати програму, що дозволяє визначати стан “життя” через вказану кількість кроків. Питання про розміри пустелі та її заповнення вирішити самостійно.

4. Існує n груп 2-го і 3-го курсів, які необхідно розподілити в n комп'ютерних класів для проведення лабораторних занять. На підставі наявних статистичних досліджень визначено продуктивність кожної групи у кожному комп'ютерному класі. Необхідно так розподілити групи по класах, щоб сумарна продуктивність на заняттях з програмування була максимальною (угорський метод розв’язанн задачі вибору: виконати крок приведення масиву і вибір незалежних нулів). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліні “Методи оптимізації”.

5. Умова завдання №4:

- реалізувати крок пошуку мінімального покриття матриці і її наступного приведення.

6. Задана “s/t - мережа”, яка складається з n міст і m дуг. Необхідно визначити величину максимального потоку в “s/t - мережі” (теорема Форда - Фалкерсона). Теоретичний матеріал див. у методичних вказівках до виконання семестрової роботи з дисципліни “Дискретна математика”.

7. Транспортна задача: вибір початкового опорного розв'язання методом північно-західного кута. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.

8. Транспортна задача: вибір початкового опорного розв'язання методом мінімального елемента. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”

9. Транспортна задача: вибір початкового опорного розв'язання методом Фогеля. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.

10. Транспортне задача: покращання опорного плану методом потенціалів. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.

11. Симплексний метод розв'язання ЗЛП: побудова симплексної таблиці, вибір розв’язувального елемента. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.

12. Симплексний метод розв'язання ЗЛП: перерахунок симплексної таблиці, визначення оптимальності одержаного розв’язку . Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.

13. Задано три послідовності: U(розмірності n), X(розмірності m), Y(розмірності r). Ураховуючи, що послідовність U – універсальна множина, послідовності X і Y – підмножини універсальної множини, необхідно знайти:

- об'єднання множин X і Y;

- перетин множин X і Y;

- різниця множин X і Y, Y і X;

- доповнення множин X і Y;

- прямий добуток множин X і Y.

Передбачити можливість некоректного завдання множин U, X, Y. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.

14. Задано дві матриці А={a_ij} розмірності nn і B={b_ij} розмірності mg. Для кожної з них поміняти місцями другий і третій стовпці та елементи рядка, який містить найбільший елемент матриці, замінити нулями. Підрахувати значення найбільшого мінора для матриць А і В.

15. Скласти функцію для підрахунку елементів матриці С={c_ij}, розмірності m g, що являється добутком матриць А={a_ij} розмірності m n і B={b_ij} розмірності n g. У масиві В поміняти місцями рядки, які вибирає користувач.

16. Скласти функцію для обчислення елементів матриці С={c_ij}, яка є сумою матриць А={a_ij} і B={b_ij} розмірності n  n. Причому матриця А може бути задана довільно, а елементи матриці B визначаються наступним чином:

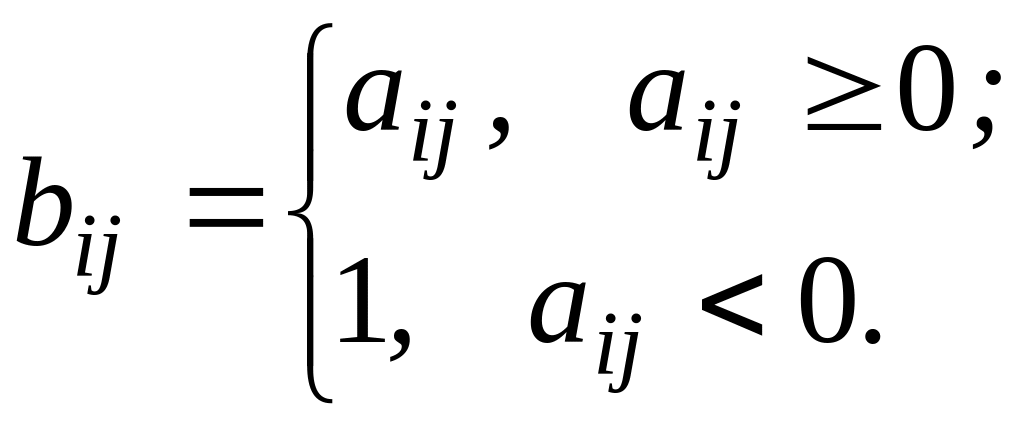
Потім у матриці А замінити всі від’ємні елементи найменшим у кожному рядку відповідно, а додатні- замінити залишком від ділення елемента на 2.

17. Скласти функцію для обчислення|підрахунку| вектора Z={z_i}, i=1..m, що дорівнює добутку матриці А={a_ij} розмірності m  n на вектор Х={х_j}, елементи якого обчислюють за формулою 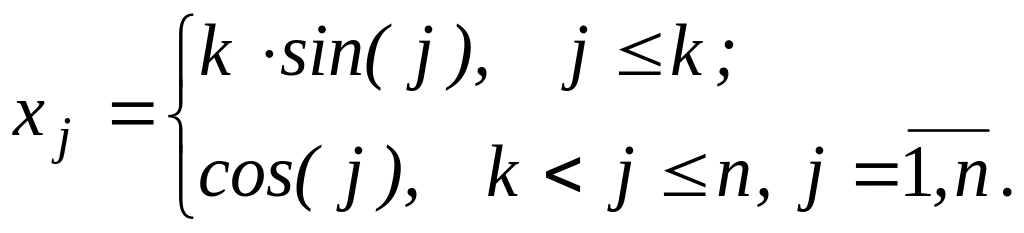Перевірити, чи являються елементи вектора Z упорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок зменшування, а також номер цього елемента, виправити порушення, тобто розташувати елементи у порядку зменшування.

18. Скласти функцію, яка у заданій матриці А розмірності mn знаходить число R - найменше з позитивних відношень, де s – номер стовпця, у якому елемент a_is є негативним. У масиві А замінити елементи стовпця знайменшим значенням нулями.

19. Написати програму, яка будує матрицю А розмірності nn з компонентами, визначуваними за формулою: a_ij= sin(i+j)x, i,j=1..n, x – довільна дійсна величина. Потім у кожному рядку А замінити найбільший елемент абсолютною величиною діагонального елемента, а від’ємні елементи замінити їх кубами. Далі розташувати елементи кожного рядка у порядку зростання.

20. У масиві А={a_ij} розмірності n  n знайти різницю між сумою і добутком елементів масиву. Потім у кожному рядку знайти найбільший елемент і впорядкувати всі елементи у правильному порядку відносно до найбільшого, тобто якщо існує рядок {1.2; 0.5; 7.0; 2.6; 5.0}, то після впорядкування має вийти рядок {0.5; 1.2; 7.0; 5.0; 2.6}.

21. Скласти функцію для обчислення матриці B={b_ij}, яка є добутком числа g на матрицю А={a_ij} розмірності n  n. Число g – найбільший елемент заданого вектора Z. Потім у матриці В замінити діагональні елементи найбільшими елементами кожного стовпця відповідно.

22. Скласти функцію для обчислення вектора B={b_i}, що дорівнює тому рядку матриці А={a_ij} розмірності n  n, у якій розташовано найбільший елемент матриці, та вектора С={c_i}, який є таким стовпцем матриці А, у якому знаходиться найменший елемент матриці. Потім упорядкувати елементи знайдених векторів у порядку зростання елементів.

23. Задано дві матриці А={a_ij} розмірності nn і B={b_ij} розмірності mg. Для кожної з них визначити добуток від’ємних елементів і їх кількість. Упорядкувати елементи рядків у матриці А і стовпців матриці В у порядку зростання лінійним швидким сортуванням.

24. Задано матрицю А={a_ij} розмірності mn. Скласти функцію для побудови логічного вектора B={b_i} за наступним правилом: якщо у рядку з номером k кількість додатних елементів більша ніж кількість від’ємних, то b_k=1(true), інакше b_k=0(false). Потім необхідно розташувати елементи кожного стовпця масиву А у порядку зменшення лінійним сортуванням.

25. Задано матрицю А={a_ij} розмірності nn. Скласти функцію для побудови вектора B={b_i} за наступним правилом: якщо a_ii0, то b_i узяти таким, що дорівнює сумі елементів і - го рядка, інакше – суму абсолютних величин і - го стовпця. Потім у матриці А розташувати елементи кожного рядка у порядку зростання.

26. Уведено матрицю А={a_ij} розмірності mn. Скласти функцію для побудови|шикування| логічного вектора B={b_i} за наступним|слідуючим| правилом: якщо і - ий рядок матриці А утворює незбутню послідовність, то b_k=1(true), інакше b_k=0(false). Потім у матриці А для кожного рядка визначити номери найменших елементів і добуток елементів, що йдуть за ними.

27. Уведено логічний вектор А={a_i} і дійсний Х={х_i} і=1.. n. Скласти функцію для перетворення вектора Х за правилом: якщо a_i=1(true), то х_i помножити на 10, інакше – розділити на -10. Потім у векторі Х замінити додатні елементи найбільшим серед додатних, а від’ємні – найменшим серед від’ємних.

28. Написати аналог гри “Хрестики - нулі”.

29. Задано куб 222, грані якого розбито на чотири однакові сектори 11. Кожний з секторів розфарбовано довільним чином. Визначити, чи розфарбовано кожну з граней куба одним кольором. Спосіб зберігання даних визначити самостійно.

30. Задано масив 33, заповнений довільно числами від 1 до 8, одна комірка масиву “умовно порожня”. Використовуючи принцип гри у квача, упорядкувати елементи масиву.