10. Кавитация

10.1. Возникновение кавитации

Явление кавитации было предсказано Л. Эйлером еще в XVIII веке и О. Рейнольдсом в 1873 году задолго до его обнаружения в 1893 году при испытании английского эскадренного миноносца «Дэринг».

Кавитацией принято называть явление разрыва сплошности в жидкости с образованием кавитационных микропузырьков, заполненных паром, газом или их смесью, обусловленное понижением давления, или так называемое «холодное кипение» жидкости.

Из интеграла Бернулли следует, что при установившемся движении жидкости распределение давлений в потоке существенно зависит от распределения скоростей. Для несжимаемой идеальной жидкости уравнение Бернулли имеет вид

Из него следует, что при движении несжимаемой идеальной жидкости в некоторых частях потока давление может получаться отрицательным или даже равняться минус бесконечности.

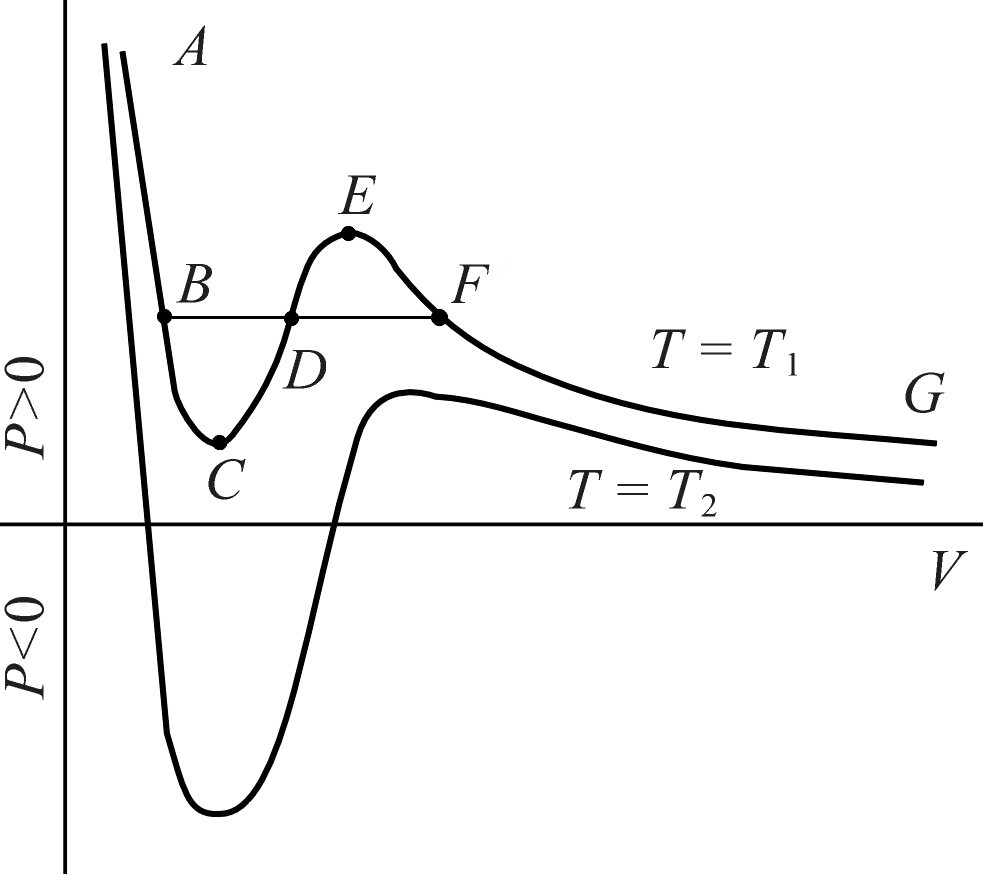
Рисунок 10.1

Диаграмма Ван-дер-Ваальса (рис. 10.1) дает представление о поведении жидкости, в которой непрерывно падает давление при постоянной температуре. Если проследить изменение давления на P–V диаграмме (рис. 10.1) от точки А до точки G по изотерме A-В-C-D-E-G, то в точке B оно достигнет той величины, при которой обычно начинается процесс парообразования. Далее проследим переход жидкости в пар при постоянном давлении (Р = const), чему соответствует линия B-D-F. После того как вся жидкость перейдет в пар, растяжение приведет к снижению давления в системе. В точке В прежде всего следует ожидать начала возникновения кавитации. В особых условиях (дегазированная жидкость, чистый сосуд, отсутствие вибрации) удается подойти через точку В к точке G, а при достаточно низких температурах (например комнатная – для воды) изотерма пересечет линию нулевого давления, т. е. в жидкости возникнут напряжения растяжения. При этом каждый элемент жидкости находится в области низкого давления лишь очень короткое время.

Известно, что воду, находящуюся в чистом сосуде под давлением в 1 атм, можно перегреть свыше 100 °С или охладить на несколько градусов ниже 0 °С. Перегрев, переохлаждение, а также перенасыщение воды газом – хорошо известные примеры метастабильных состояний. Для метастабильности характерно следующее свойство: вещество мгновенно выводится из метастабильного состояния при возникновении зародышей (с размерами, большими критической величины для данных условий) другой фазы.

Практический опыт учит тому, что жидкости не могут сопротивляться сколько-нибудь значительным напряжениям растяжения. Однако впервые в 1843 году Ф. Донни установил возможность метастабильного состояния жидкостей, при котором в них действуют растягивающие напряжения.

Максимальные растягивающие напряжения были замерены Л. Бриггсом центробежным методом. В опытах со ртутью ему удалось достичь значений растягивающих напряжений 4,210⁷ Па, а с водой – 2,810⁷ Па. Согласно кинетической теории жидкостей, чистые жидкости способны выдерживать очень высокие растяжения (отрицательные давления): от 50 до 1000 мПа. В настоящее время не выяснено, предельны ли полученные Л. Бриггсом значения растягивающих напряжений.

Самая простая теоретическая оценка разрывных напряжений сделана на основании предположения, что разрыв происходит на микрополостях, размер которых по порядку величины равен среднему расстоянию между молекулами. Предположив, что разрыв произойдет тогда, когда разрывные напряжения достигнут величины капиллярных сил на поверхности пузырька, которым условно заменяется микрополость, мы можем определить величину этих напряжений с помощью формулы Лапласа:

, (10.1)

где  капиллярная постоянная; R – радиус полости, или пузырька. Исходя из этой формулы, для воды ( ) получим значение Па.

В отличие от специально поставленных лабораторных опытов с прецизионно чистой (химически и механически) водой в обычных условиях, как правило, не удается зафиксировать сколько-нибудь заметных растягивающих напряжений. В быту, технике и природе не встречаются жидкости с высокой степенью чистоты, что является непременным условием ранее указанных физических опытов. Поэтому давление в обычном потоке не может быть ниже некоторой положительной величины , близкой при обычной температуре (20 °С) к нулю, т. е. к давлению насыщенных паров жидкости, которое зависит от температуры и свойств жидкости.

Когда давление в потоке падает до значения , нарушается сплошность течения и образуется область, заполненная паровыми или газовыми пузырьками, т. е. осуществляется фазовый переход первого рода в условиях умеренных или низких температур или кавитации («холодное кипение»).

Теоретически холодное кипение в жидкости начинается при . Если в жидкости много растворенного воздуха, снижение давления приводит к его выделению и образованию газовых каверн, в которых давление выше, чем давление насыщенных паров жидкости. При наличии в жидкости микроскопических пузырьков кавитация может возникать в условиях .

Вместе с тем, как отмечает академик Л. И. Седов, практика и физические теории указывают на то, что даже в обычных условиях в короткие промежутки времени в жидкости могут возникать ограниченные по величине отрицательные давления, вызывающие внутренние растяжения, при отсутствии действительных разрывов и кипения. Например, обычная водопроводная вода может выдерживать очень короткое время растяжение до 4 атм.

Очевидно, что причиной низкой объемной прочности в повседневной практике является загрязненность жидкости другими веществами и нерастворенными частицами. Их наличие приводит к появлению в жидкости слабых мест, получивших название кавитационных зародышей, или ядер кавитации (гипотеза Л. А. Эпштейна – Гарвея). Детальная структура ядер окончательно не установлена. Малые размеры и неопределенность пространственного положения их существенно затрудняют наблюдение за ними.

В инженерных расчетах принимают, что кавитация возникает при падении давления в жидкости до , т. е.

(10.2)

где  критическое значение кавитации;  давление в невозмущенном потоке.

Под ядрами кавитации в настоящее время понимают:

– газовые микропузырьки, внесенные из атмосферы;

– твердые частицы с микротрещинами, внесенные извне и образовавшиеся в результате деятельности биоорганизмов;

– микротрещины в твердых поверхностях, заполненные парогазом;

– паровые пузырьки, образующиеся при ионизирующем воздействии космического излучения (в частности при вторично-нейтронном облучении);

– паровые пузырьки, возникающие при гетерофазных флуктуациях (в результате объединения молекул с повышенной энергией – гомогенная нуклеация или образующиеся на примесных частицах или молекулах растворенных газов – гетерогенная нуклеация).

При этом имеет место статически-динамическое равновесие. Поэтому при определении кавитационной прочности реальной жидкости необходима фиксация конкретных зародышей (например спектров парогазовых микропузырьков лазерно-галографическими или радиоэлектронными способами по индикатрисам рассеяния).

Каждый кавитационный пузырек, формируясь из ядра, растет до конечных размеров (первая стадия «жизни» пузырька), после чего схлопывается. Две фазы существования пузырька – расширение и схлопывание – образуют полный термодинамический цикл. Схлопывание пузырька сопровождается люминесцентными и акустическими эффектами, а также резким повышением температуры и давления в малой окрестности вблизи пузырька. Причем схлопывание пузырька около твердых стенок происходит не симметрично, а с образованием так называемой кумулятивной струйки.