9.10. Теплоотдача при поперечном обтекании цилиндра

Как показывают исследования, интенсивность теплообмена для отдельных мест цилиндра, обтекаемого поперечным потоком жидкости, весьма неравномерна. По мере удаления от лобовой образующей, вблизи которой происходит разветвление потока, местный коэффициент теплоотдачи уменьшается в связи с нарастанием пограничного слоя. Такое изменение этой величины имеет место вплоть до точки отрыва пограничного слоя, которая при докритических значениях числа Рейнольдса (т. е. при ламинарном пограничном слое) лежит несколько впереди экваториального сечения (рис. 9.11). За этой точкой начинается возрастание коэффициента теплоотдачи, обусловленное вихреобразованием в кормовой области цилиндра.

Такой характер распределения коэффициента теплоотдачи сохраняется до тех пор, пока . При пограничный слой турбулизуется и точка отрыва его смещается ближе к кормовой части цилиндра. В этом же направлении сдвигается и точка минимума коэффициента теплоотдачи. Поскольку отрыв турбулентного пограничного слоя связан со значительно более интенсивным вихреобразованием, чем отрыв ламинарного слоя, то и коэффициент теплоотдачи возрастает в этом случае более резко.

Зависимость между средним значением числа Нуссельта и критерием Рейнольдса для случая поперечного обтекания цилиндра воздухом (Рr = 0,72) может быть выражена формулой

, (9.65)

где С и – постоянные, зависящие от числа Рейнольдса. Их значения даны в таблице.

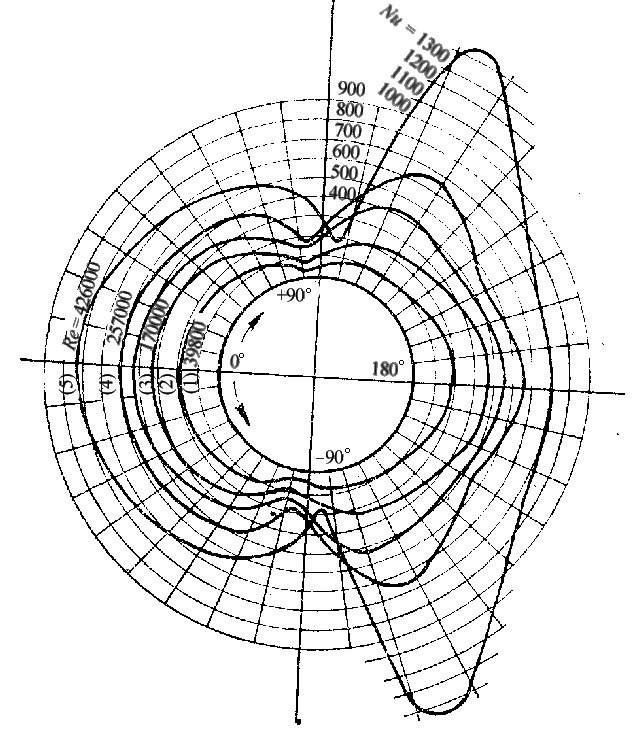
Рисунок 9.11

Таблица

	5–80	80–5·103	5·103–5·104	> 5·104
С	0,81	0,695	0,197	0,023
	0,40	0,46	0,60	0,80

Для поперечного обтекания цилиндра другими газами или жидкостями с может быть рекомендована формула

(9.66)

в которой постоянные С и сохраняют прежние значения.

Численные значения физических постоянных и в формулах (9.65) и (9.66) относятся к средней температуре потока.

 Более строго интенсивность этих двух процессов следует поставить в связь с существованием теплового и диффузионного пограничных слоев, о которых речь пойдет в дальнейшем.

 Вообще говоря, толщина пограничного слоя является величиной условной, поскольку скорость V₁ по мере удаления от поверхности приближается к значению U асимптотически. Обычно принято определять  как расстояние от поверхности, на котором V₁ = (0,980,99)U.

* Это дополнительное условие непосредственно вытекает из уравнения (9.15), если учесть, что при не только , но и .

* Это дополнительное условие непосредственно вытекает из первого уравнения системы (9.31) при применении к нему рассматриваемого граничного условия.

217