9.4. Начальный участок в цилиндрической трубе при ламинарном режиме движения жидкости
Если жидкость поступает в трубу из резервуара большой емкости, то во входном сечении трубы распределение скоростей будет почти равномерным. По мере удаления от входного сечения происходит разрастание ламинарного пограничного слоя. Так как расход жидкости должен быть во всех сечениях трубы одинаков, то торможение жидкости, имеющее место в пограничном слое, должно компенсироваться увеличением скорости в ядре потока. Благодаря этому кривые распределения скоростей приобретают вид, показанный на рис. 9.4.
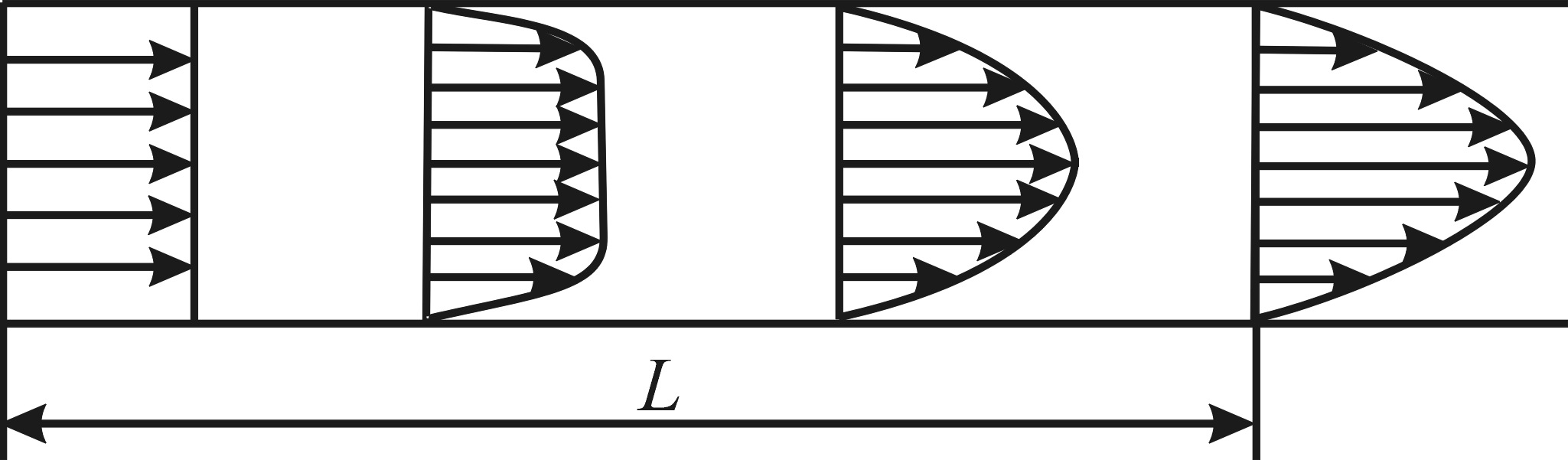
Рисунок 9.4
Участок трубы, в конце которого по всему сечению устанавливается параболическое распределение скоростей, характерное для ламинарного режима движения, получил название начального участка.
Полагая, что общие закономерности, которым подчиняется формирование ламинарного пограничного слоя в трубе, остаются такими же, как для плоской пластинки, можем в соответствии с уравнением (9.22) написать
или
.
Обозначая длину
начального участка через
и считая, что при x1
= L
,
получим
.
Таким образом, длина входного участка является функцией числа Рейнольдса. По Шиллеру,
.
9.5. Тепловой ламинарный пограничный слой на плоской пластинке, обтекаемой в продольном направлении
Если поверхность тела обтекается потоком жидкости с температурой, отличающейся от температуры самого тела, то у поверхности тела образуется тепловой дограничный слой, в котором сосредоточивается разность этих температур. В пределах этого слоя, сходного с гидродинамическим пограничным слоем, наряду с конвекцией тепла существенное значение имеет перенос тепла молекулярной теплопроводностью. Роль этой формы переноса тепла возрастает по мере приближения от внешней границы теплового пограничного слоя к поверхности тела, где она становится единственно возможной. За пределами теплового пограничного слоя процесс молекулярной теплопроводности играет ничтожную роль по сравнению с конвекцией тепла.
Тепловой пограничный слой, как и его гидродинамический аналог, может быть и ламинарным, и турбулентным. Здесь мы рассмотрим ламинарный тепловой пограничный слой, который образуется на плоской пластинке при продольном обтекании ее стационарным двухмерным потоком несжимаемой жидкости.
Система уравнений, описывающих процесс конвективной теплопроводности, для данного случая упрощается. Для уравнения Навье Стокса, входящего в состав этой системы, упрощения уже были сделаны применительно к гидродинамическому пограничному слою. Подобным же образом может быть упрощено и собственно уравнение конвективной теплопроводности. Перепишем это уравнение в координатной форме
(9.28)
и преобразуем его к безразмерному виду.
Для этой цели
воспользуемся в качестве множителей
преобразования протяженностью пластинки
в направлении обтекания
,
скоростью набегающего потока
и его температурой
(температура среды);
получим
,
следовательно,
или после деления на множитель при левой части уравнения
или, наконец,
(9.29)
где
– критерий Пекле.
Обозначим толщину
теплового пограничного слоя через
и сохраним за толщиной гидродинамического
пограничного слоя его прежнее обозначение
.
Безразмерная толщина теплового
пограничного слоя будет
=
.
Оценим порядок
величины отдельных членов, входящих в
уравнение (9.29). При этом
будем иметь в виду, что, как уже было
установлено, порядок величины
равен
,
а предельное значение координаты
имеет для теплового пограничного слоя
порядок
.
Величины
и
,
как было показано ранее, изменяются в
пределах от нуля до единицы; предельное
изменение температуры в тепловом
пограничном слое является величиной
конечной и его порядок также можно
положить равным единице.
Подпишем под каждым членом уравнения (9.29) порядок величины его сомножителей:
Поскольку
,
то очевидно, что в правой части этого
уравнения можно пренебречь производной
по сравнению с
.
Далее, поскольку порядок обеих частей
уравнения должен быть одинаковым, можно
утверждать, что величина 1/Ре должна
иметь порядок, равный
,
т. е.
Отсюда находим
или
что равносильно
(9.30)
где
критерий Прандтля.
Как будет показано
в дальнейшем, найденный здесь характер
зависимости
от числа Рейнольдса подтверждается
расчетом, тогда как зависимость этой
величины от числа Прандтля оказывается
несколько иной.
Перепишем уравнение (9.29), возвращая ему размерную форму и исключая опущенную производную, стоящую в скобках, получим
В таком виде это уравнение должно быть включено в систему уравнений конвективного переноса тепла. Уравнение движения жидкости должно быть в этой системе также представлено в упрощенной форме, а именно в форме (9.15), найденной для пограничного слоя на плоской пластинке.
Таким образом, для ламинарного теплового пограничного слоя будем иметь следующую систему уравнений:
(9.31)
при граничных условиях:
(9.32)
Здесь
температура поверхности пластинки.
Из сопоставления
граничных условий для
и Т следует, что решение системы
уравнений (9.31) возможно
лишь для случаев, когда
.
Будем решать эту систему приближенным методом, сведя уравнение конвективной теплопроводности к интегральному соотношению, схожему по своему виду с уравнением импульсов Кармана.
Для этой цели преобразуем указанное уравнение к виду
В силу уравнения неразрывности член этого уравнения, который содержит в качестве сомножителя сумму производных, стоящую в скобках, равен нулю.
Далее запишем уравнение неразрывности в форме
и вычтем из него предыдущее уравнение, тогда получим
Будем отсчитывать
температуру от температуры поверхности
и введем следующие обозначения:
;
.
Теперь последнее уравнение запишется
в виде
(9.33)
а граничные и дополнительные условия к нему приобретут вид, аналогичный тем, которые привлекались к решению задачи о гидродинамическом пограничном слое, т. е.
(9.34)
Интегрируя уравнение (9.33) по в пределах от нуля до , получаем
(9.35)
Интеграл, записанный в левой части этого уравнения, подобен тому, который встречался при выводе уравнения импульсов, и может быть представлен в виде
Используя граничные условия (9.34), находим
Подстановка полученных равенств в уравнение (9.35) дает
Разделив обе части
этого уравнения на
и имея при этом в виду, что для случая
обтекания плоской пластинки скорость
потенциального потока
есть величина постоянная, получим
интегральное соотношение для теплового
пограничного слоя, аналогичное уравнению
импульсов Кармана,
(9.36)
Полином, при помощи которого может быть выражено распределение температуры в тепловом пограничном слое, должен в соответствии с числом привлекаемых граничных и дополнительных условий состоять из четырех членов:
(9.37)
В силу тождественности вида этого полинома и граничных условий (9.34) с таковыми для скорости в гидродинамическом пограничном слое [уравнения (9.18) и (9.17)] должны быть тождественны по форме и выражения для температурного и скоростного полей в соответствующих пограничных слоях. Поэтому мы можем, опуская детальные вычисления, по аналогии с уравнением (9.19) написать
(9.38)
Используя выражения (9.19) и (9.38), вычислим интеграл, входящий в уравнение (9.36); получим
где
.
Поскольку мы
приняли, что
и, следовательно,
,
то вторым членом в скобках можно
пренебречь по сравнению с первым.
Далее, дифференцируя выражение (9.38), находим значение производной, стоящей в правой части уравнения (9.36):
. (9.39)
Если вычисленные значения интеграла и производной подставить в уравнение (9.36), то получим
,
или
(9.40)
В случае когда
тепловой пограничный слой зарождается
одновременно с гидродинамическим у
передней кромки пластинки, отношение
их толщин
не должно зависеть от
,
т. е.
.
Если, кроме того, учесть, что в соответствии
с равенством (9.21)
то уравнение (9.40) приобретет вид
Принимая
14/13
1
и замечая, что
,
получаем
,
или
(9.41)
Это равенство уточняет оценку порядка зависимости величины от критерия Прандтля, данную в выражении (9.30).
Подставляя в равенство (9.41) значение из выражения (9.23), получим формулу для толщины ламинарного теплового пограничного слоя
(9.42)
Так как эта формула получена в предположении, что Т / 1, то она применима лишь для случаев, когда Pr 1, т. е. для газов и неметаллических жидкостей.
Зная
,
можно определить значение местного
коэффициента теплоотдачи
.
Примем для определенности, что
.
Имеем
или
или, наконец, учитывая равенство (9.39),
(9.43)
Отсюда видно, что местный коэффициент теплоотдачи обратно пропорционален толщине теплового пограничного слоя. Подставляя в (9.43) значение из уравнения (9.42), получим
.
Как и для формулы (9.25), более точный расчет несколько исправляет численный множитель в формуле (9.44), давая
. (9.44)
Обычно вместо
пользуются более удобным для расчетов
средним по длине пластинки значением
коэффициента теплоотдачи, за которым
мы сохраним обозначение
и который определяется как
или, учитывая равенство (9.44),
Этому уравнению можно придать безразмерную форму:
(9.45)
Определив из этого
уравнения число Нуссельта, можно найти
количество тепла, отдаваемого жидкости
одной стороной пластинки шириною, равной
,
в единицу времени:
(9.46)