9. Пограничный слой и процессы тепло- и массообмена

9.1. Понятие о пограничном слое

Ранее отмечалось, что при очень больших значениях числа Рейнольдса, свидетельствующих о большом преобладании инерционных сил над силами вязкости, можно последними пренебречь и рассматривать движущуюся жидкость при таких Re как идеальную. Однако такое приближение не может быть распространено на ту область течения жидкости, которая непосредственно примыкает к поверхности твердого тела и на которой сказывается тормозящее влияние поверхности. В этой, вообще говоря, узкой области имеет место резкое изменение скорости по нормали к поверхности от нулевого значения, которое она имеет на самой поверхности, до значения, сравнимого с тем, которое устанавливается вдали от поверхности. Этот тонкий слой жидкости получил название пограничного слоя. В этом слое пренебрегать силами вязкости нельзя. Наоборот, благодаря большим градиентам скорости они приобретают здесь решающее значение. Но сведение сферы влияния этих сил к узкой области пограничного слоя позволяет внести значительные упрощения в уравнения движения вязкой жидкости и делает возможным их интегрирование.

Явления, происходящие в пограничном слое, играют существенную роль как в определении величины гидродинамического сопротивления, так и в определении интенсивности процессов тепло- и массообмена между твердым телом и обтекающей его жидкостью^.

Движение жидкости в пограничном слое может быть как ламинарным, так и турбулентным.

9.2. Уравнения ламинарного пограничного слоя

для более легкого восприятия рассмотрим двухмерное обтекание плоской поверхности тела несжимаемой жидкостью. Направим ось вдоль поверхности по направлению потока, а ось – перпендикулярно к поверхности (рис. 9.1). Будем полагать поток стационарным и массовые силы отсутствующими. Тогда уравнения Навье  Стокса и уравнение неразрывности принимают вид

(9.1)

Обозначим скорость за пределами пограничного слоя (иными словами, скорость набегающего потока) через U. Поскольку вне пограничного слоя жидкость рассматривается как идеальная, движение частиц которой происходит без деформации и, следовательно, не сопровождается вращением, то в указанной области поток можно считать потенциальным.

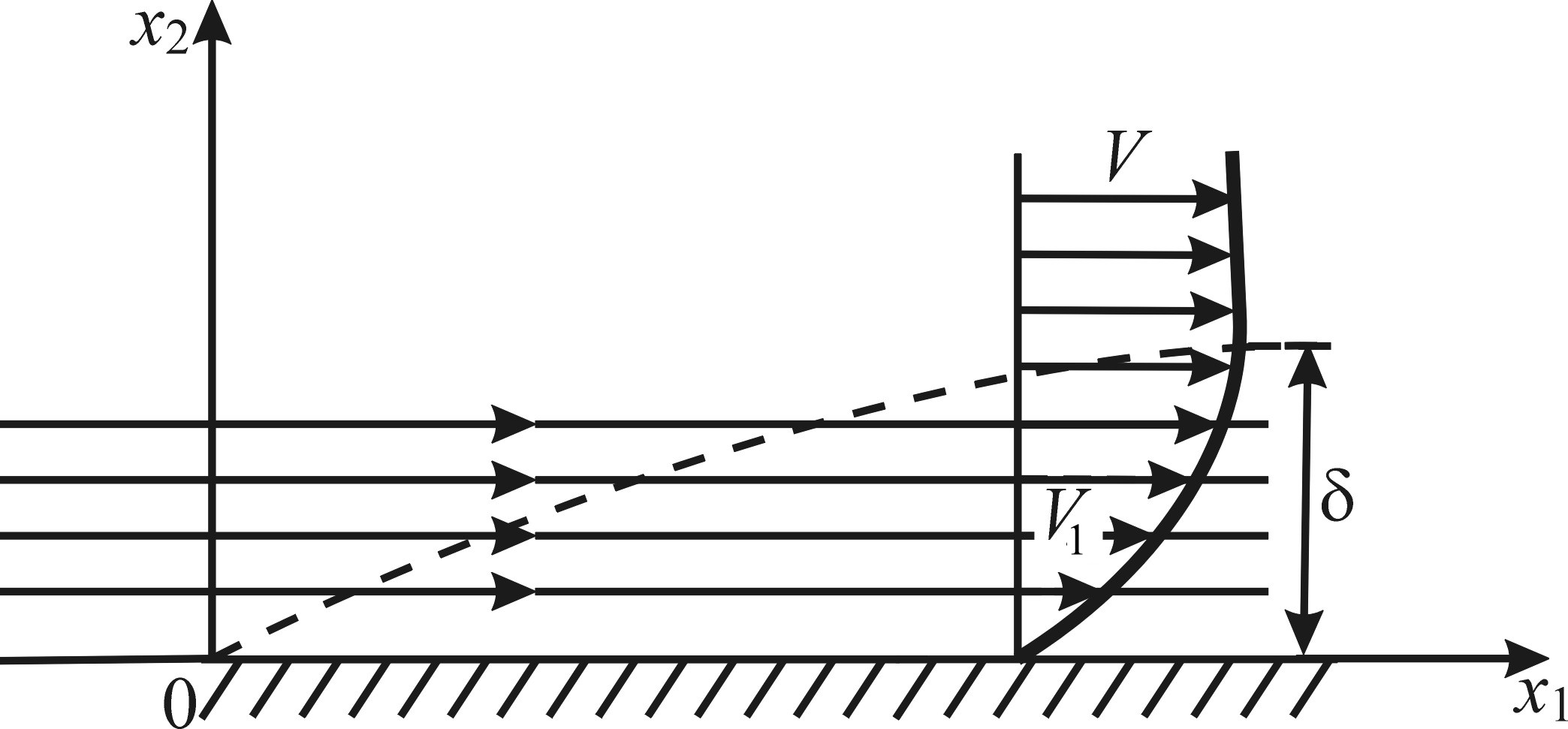
Рисунок 9.1

Преобразуем систему уравнений (9.1) к безразмерному виду, воспользовавшись для этой цели в качестве характерных величин протяженностью поверхности тела в направлении обтекания и скоростью набегающего потенциального потока ; в качестве масштаба преобразования давления выберем удвоенный динамический напор потока . Тогда будем иметь

Подставив соответствующие величины в первое из уравнений системы (9.1), получим

или после деления обеих частей уравнения на

.

Придав аналогичный вид второй компоненте системы (9.1), преобразуя к безразмерной форме уравнение неразрывности и замечая, что – число Рейнольдса, определенное по скорости набегающего потока, получим

(9.2)

Такая форма записи уравнений движения удобна для анализа порядка величины отдельных членов, входящих в эти уравнения, и для выявления тех упрощений, которые могут быть сделаны при применении этих уравнений к пограничному слою.

Обозначим толщину пограничного слоя через и будем понимать под этой величиной то расстояние от поверхности, на котором скорость становится близка к скорости основного (набегающего) потока^.

Прежде чем приступить к анализу уравнений (9.2), отметим, что безразмерная координата изменяется в пределах от нуля до единицы (при ). Безразмерной координатой приходится в данной задаче оперировать только в пределах пограничного слоя, где ее значение изменяется в интервале от нуля до , здесь  безразмерная толщина пограничного слоя.

Безразмерная компонента скорости изменяется в пределах от нуля до единицы (при , т. е. на внешней границе пограничного слоя).

Обратимся теперь к уравнению неразрывности

Определяя порядок производной как отношение предельных изменений величин и , находим, что он равен единице. Из рассматриваемого уравнения следует, что производная также имеет порядок, равный единице, а так как предельное значение безразмерной координаты равно , то и предельный порядок величины будет таким же.

Запишем теперь под членами первых двух уравнений системы (9.2) их порядки и при сопоставлении отдельных членов этих уравнений друг с другом будем считать . Производную , поскольку она не связана с , следует рассматривать как величину конечную, и ее порядок можно положить равным единице. Относительно порядка производной нельзя сделать никаких предварительных предположений. Таким образом, можем написать

Очевидно, что в правой части первого уравнения можно пренебречь величиной по сравнению с  величиной, порядок которой много больше единицы. Из этого уравнения следует, что величина должна иметь порядок, равный единице, т. е. такой же, как и все остальные члены этого уравнения:

.

Отсюда вытекает, что порядок величины равен , а или, учитывая, что ,

(9.3)

Поскольку в основе теории пограничного слоя лежит предположение о том, что число Рейнольдса, характеризующее поток, велико, то из соотношения (9.3) становится очевидным, что толщина пограничного слоя представляет ничтожно малую величину по сравнению с размерами обтекаемого тела. Как будет видно из дальнейшего, порядок зависимости от числа , выраженный соотношением (9.3), подтверждается точным расчетом.

Обратимся теперь ко второму уравнению. Порядок членов, содержащихся в левой части этого уравнения, равен , слагаемые, стоящие в скобках, после умножения на приобретают соответственно порядки и , поэтому производная также должна иметь порядок . Следовательно, рассматриваемое уравнение можно полностью отбросить и, в частности, пренебречь изменением давления в пограничном слое в направлении, нормальном к поверхности, считая, что .

Это означает, что в принятом приближении давление в пограничном слое остается таким же, как вне пограничного слоя, и является функцией только координаты х. Поэтому в первом уравнении системы (9.2) можно вместо частной производной написать полную производную .

Таким образом, из системы уравнений (9.2) второе уравнение можно целиком исключить, а в первом сделать указанные упрощения. Возвращая оставшимся уравнениям размерную форму, получим

(9.4)

Уравнения (9.4) называются уравнениями Прандтля для пограничного слоя. Будучи получены из уравнения Навье  Стокса, в котором пульсационные скорости в явной форме не представлены, они пригодны лишь для описания движения в ламинарном пограничном слое.

Применим к внешней границе пограничного слоя уравнение Бернулли  Эйлера для потенциального потока (5.63), в котором для данного случая геометрический напор рассматривается как величина постоянная:

.

Дифференцируя это уравнение по , находим, что

.

Подставляя это выражение в уравнение Прандтля, получим систему уравнений ламинарного пограничного слоя в более удобной форме:

(9.5)

Эти уравнения, полученные для случая обтекания плоской поверхности, пригодны и для искривленных поверхностей, если радиус кривизны намного превосходит толщину пограничного слоя .

Граничные условия для этих уравнений имеют вид

(9.6)

Наиболее простой, но приближенный метод решения системы уравнений (9.5) основан на сведении этой системы к так называемому уравнению импульсов Кармана. Преобразуем инерционные члены, входящие в первое уравнение системы (9.6), следующим образом:

Тогда можем записать

или, используя уравнение неразрывности,

(9.7)

Далее запишем уравнение неразрывности в форме

где член равен нулю, a поскольку скорость набегающего потока от координаты не зависит, и вычтем из этого уравнения выражение (9.7). Тогда будем иметь

(9.8)

Проинтегрировав это уравнение по в пределах от нуля до толщины пограничного слоя , получим

(9.9)

При интегрировании следует учесть, что является величиной переменной, зависящей от координаты .

Первый интеграл представляет одно из слагаемых производной, взятой по координате от интеграла с переменным верхним пределом:

Следовательно,

При интегрировании уравнения (9.9) используем граничные условия (9.6), присоединив к ним некоторые дополнительные условия:

(9.10)

Находим значения отдельных составляющих уравнения (9.9):

После подстановки всех последних равенств уравнение приобретет вид

или

(9.11)

Введем следующие обозначения:

(9.12)

(9.13)

Первый из этих интегралов получил название толщины вытеснения, а второй – толщины потери импульса. Подставив эти величины в уравнение (9.11), придадим ему вид

или после дифференцирования первого слагаемого

(9.14)

Полученное уравнение и есть уравнение импульсов Кармана, являющееся основным интегральным соотношением для ламинарного пограничного слоя.

Рассмотрим физический смысл величин и . Перепишем равенство (9.12) в следующей форме:

.

Содержание интеграла можно представить себе как связанную с уменьшением скорости потерю объемного расхода жидкости через сечение в пограничном слое, отнесенного к ширине поверхности, равной единице. Графически этот интеграл определяется площадью, которая ограничивается кривой распределения скоростей, абсциссой и асимптотой (рис. 9.2).

Левая часть последнего равенства показывает, что такая же потеря расхода имела бы место в том случае, если бы жидкость в пограничном слое вела себя как идеальная и ее скорость в этой области была бы всюду равна скорости основного потенциального потока , но поток оказался бы смещенным от поверхности на расстояние . Величина может быть определена из условия равновеликости заштрихованных площадей.

Аналогичный смысл имеет и величина . Ее можно понимать как некоторую эквивалентную толщину, отвечающую уменьшению потока импульса (количества движения), обусловленному вязкостью.

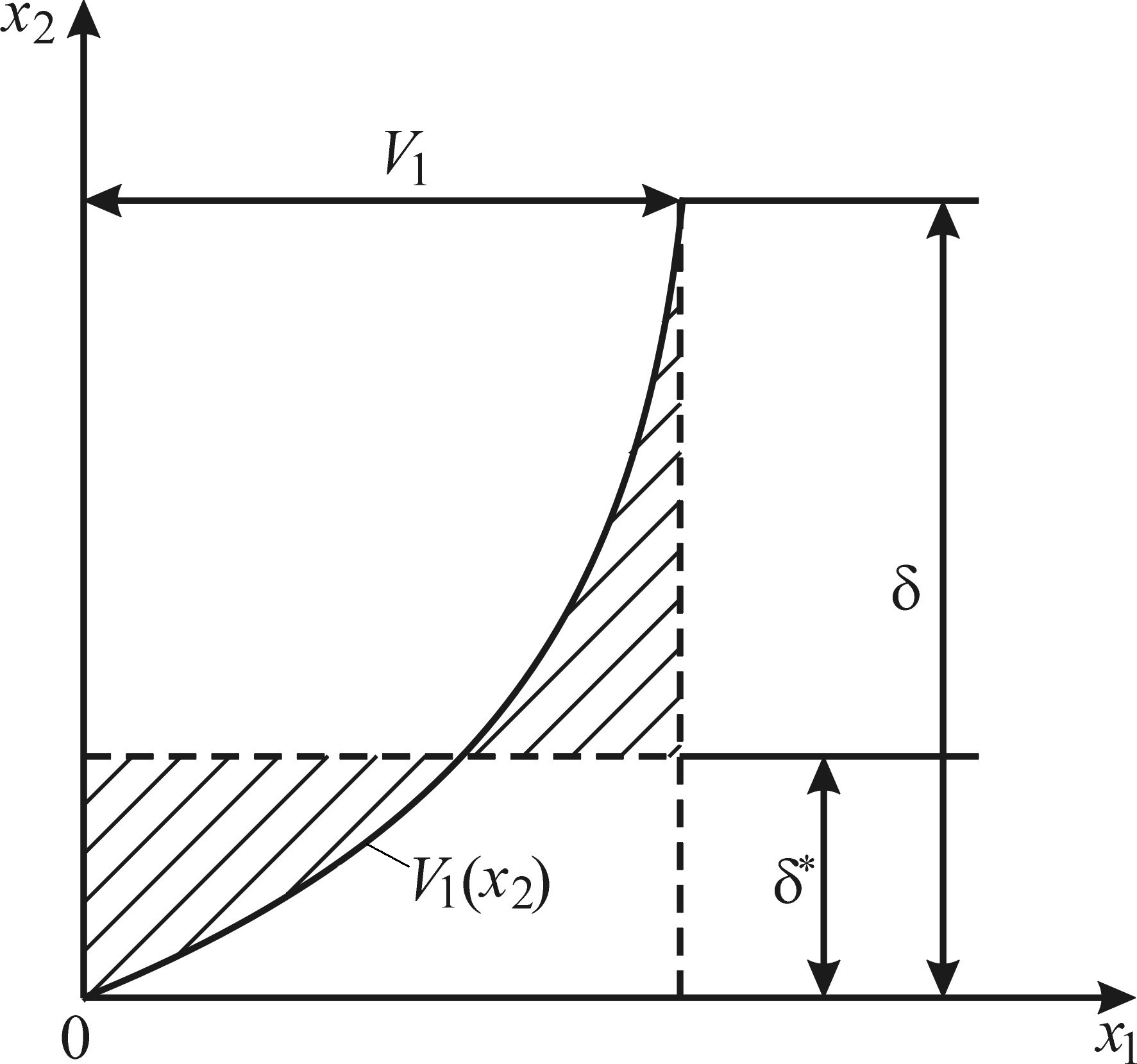
Рисунок 9.2