5.5. Формы записи уравнений движения в различных системах координат (инерциальных и неинерциальных)

Предыдущие законы и уравнения записывали в абсолютно неподвижной системе для любой инерциальной системы координат (согласно третьему постулату Галилея  Ньютона). Покажем это конкретно. Пусть система координат инерциальна, т. е. движется равномерно и поступательно с постоянной скоростью . Тогда

, (5.38)

где  относительная скорость.

Так как для такой инерциальной системы координат

и ,

то

; (5.39)

(5.40)

Следовательно, уравнения движения в напряжениях не изменяют свой вид:

(5.41)

. (5.42)

Итак, индекс r переносного движения для инерциальной системы координат можно опускать. Однако для неинерциальных систем координат (движущейся неравномерно или с вращением) этого сделать нельзя. Покажем это. Пусть переносная скорость

(5.43)

Тогда абсолютная скорость представима так:

= (5.44)

или

= , (5.45)

(5.46)

Можно установить, что

, (5.47)

и уравнения абсолютного движения в напряжениях, но для неинерциальной системы координат, примут вид

(5.48)

которым можно придать и другую форму:

. (5.49)

Уравнение (5.49) часто используют для описания абсолютного движения в относительной системе координат.

Покажем также запись относительного движения в относительной (неинерциальной) системе координат, что очень удобно при описании движения жидкости во вращающихся механизмах (планетарных задачах в масштабах вращающейся Земли и др.). Напомним основные положения теоретической механики об абсолютном, переносном и относительном движениях:

; (5.50)

, (5.51)

где

и ;

(5.52)

где  соответственно переносное, кориолисово и относительное ускорения. Причем (см. рис. 5.5)

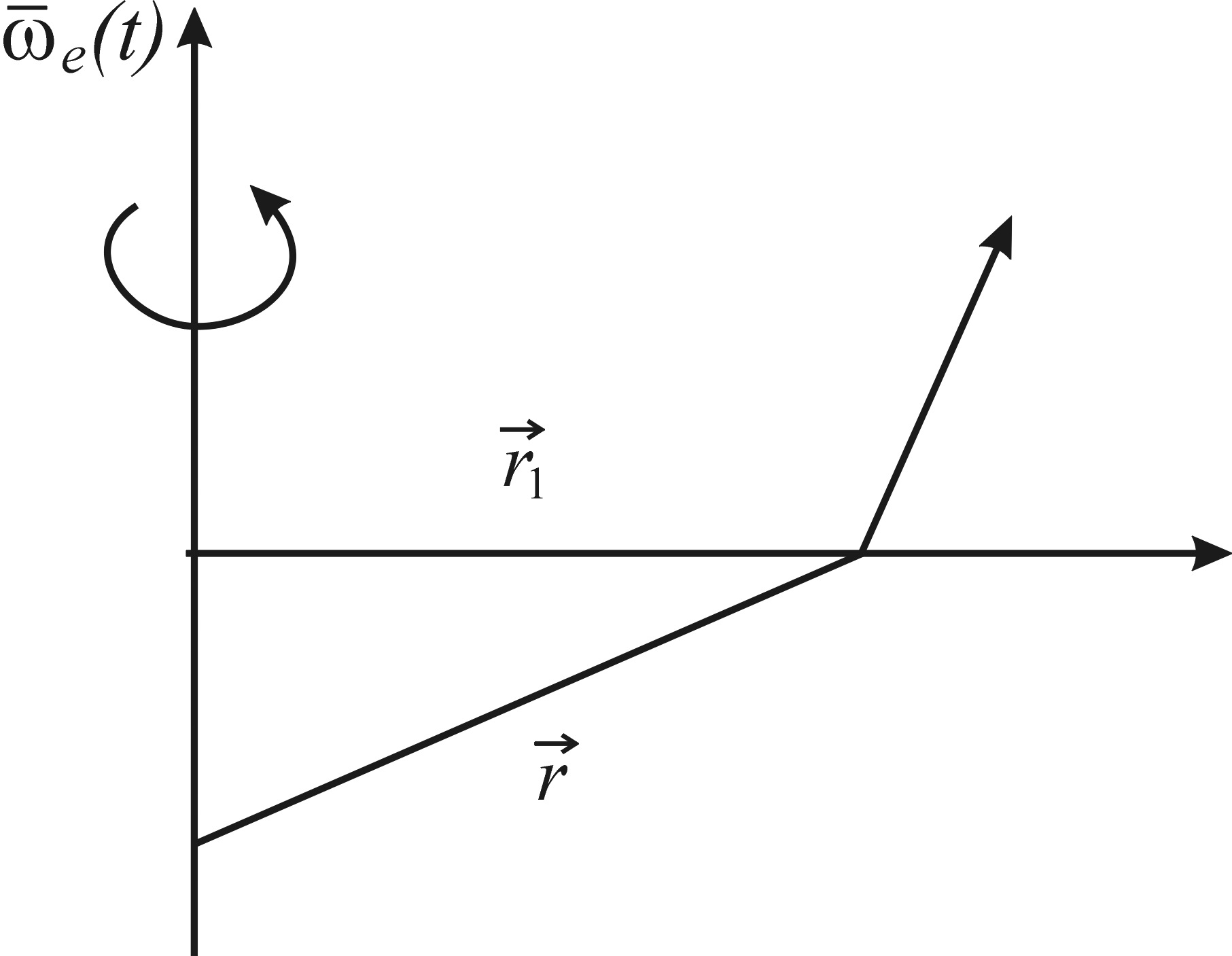
Рисунок 5.5

,

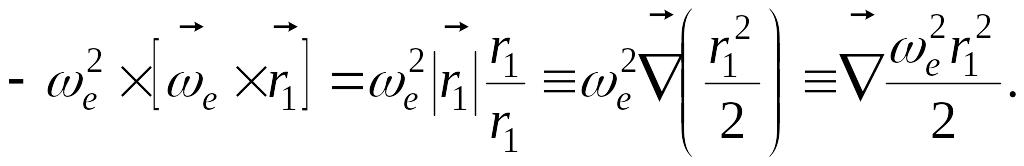
По формуле Эйлера имеем для относительной системы координат

, (5.53)

или, с использованием тождества Громеки  Лэмба

. (5.54)

После чего уравнения движения в напряжениях (5.27) примут форму

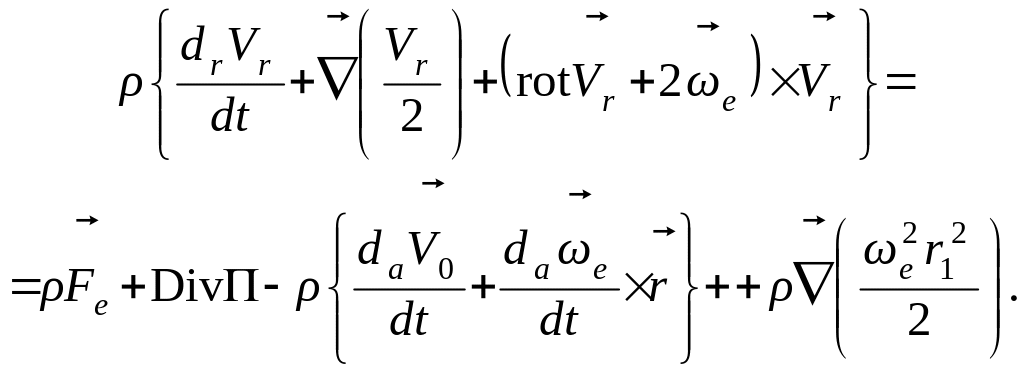(5.55)

Если инерциальная система движется равномерно ( ) и вращается, но с постоянной угловой скоростью ( ), то

, ,

а кроме того, и Для такой системы координат окончательно будем иметь

(5.56)

где последний член – объемная плотность центробежных сил с потенциалом . Для идеальной баротропной жидкости в поле консервативных объемных сил ( ) будем иметь эти же уравнения в форме Озеена (для относительного движения):

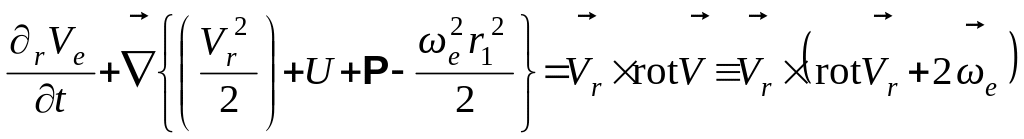(5.57)

при и . Из сопоставления (5.45) и (5.52) можно установить, что

(5.58)

то есть

(5.59)

Для инерциальной системы координат ( и ) формула (5.59) обращается в тождество вида 0 0, а (5.58) переходит в ранее полученное соотношение (5.52).

5.6. Первые интегралы уравнений движения Эйлера

Для идеальной ( ; ) баротропной жидкости в поле консервативных сил можно получить первые интегралы уравнений движения Эйлера, записанные в форме Озеена – в абсолютной, или инерциальной, системе координат, а также для относительного движения. Выпишем эти уравнения:

; (5.60)

. (5.61)

Интеграл Бернулли. Предположим, что течение стационарно, т. е. . Умножим левую и правую части уравнения (5.60) скалярно на , причем все перемещения направлены вдоль линии тока, когда . Тогда в правой части (5.60) получим тождественный нуль, а в левой части

(5.62)

Следовательно, плотность механической энергии

, или , (5.63)

остается постоянной вдоль линии тока, а на каждой из линий тока может быть свое значение для всех ее точек.

Уравнение Бернулли, полученное как первый интеграл уравнений Эйлера, означает ничто иное, как утверждение о сохранении механической энергии. В соответствии с этим первые два слагаемых в (5.63) представляют собой соответственно потенциальную энергию положения и объемного действия поверхностных сил, а третье – удельную кинетическую энергию (см. вторую форму записи).

При записи уравнения Бернулли в виде

слагаемые трехчлена называют соответственно геометрическим, пьезометрическим и скоростным напорами.

Уравнение Бернулли можно использовать для расчетов гидромашин (рабочих колес гидротурбин, насосов и т. д.) в случае относительного движения жидкости в равномерно вращающейся вокруг неподвижной оси системе координат. В относительной системе координат, например связанной с вращающимся рабочим колесом, поток жидкости стационарен, и применение теоремы Бернулли возможно (в отличие от абсолютного потока).

Если аналогичную процедуру выполнить для уравнений (5.61), т. е. интегрируя вдоль линий тока относительного движения, то

. (5.64)

При стационарном течении в относительной системе координат в силу (5.64) уравнения (5.61) дают  условие Н. Е. Жуковского (Ф. И. Франкль и М. В. Келдыш в 1935 г. показали, что это условие является первым, но достаточно сильным приближением). Это означает, что вихри абсолютного движения располагаются вдоль линий тока относительного движения:

. (5.65)

При малых нагрузках , т. е.

,

условие Н. Е. Жуковского переходит в линеаризированное условие

(5.66)

Это означает, что вихри абсолютного движения при малых нагрузках располагаются примерно вдоль линии тока переносного течения, которое всегда известно.

Интеграл Громеки. При стационарном течении можно интегрирование (5.60) провести и вдоль вихревых линий, принимая . Тогда

(5.67)

будет вдоль вихревых линий, где  одна и та же для всех геометрических точек на одной и той же вихревой линии. Если линии тока и вихревые линии образуют поверхности (рис. 5.6), то для них очевидно, что ;

Рисунок 5.6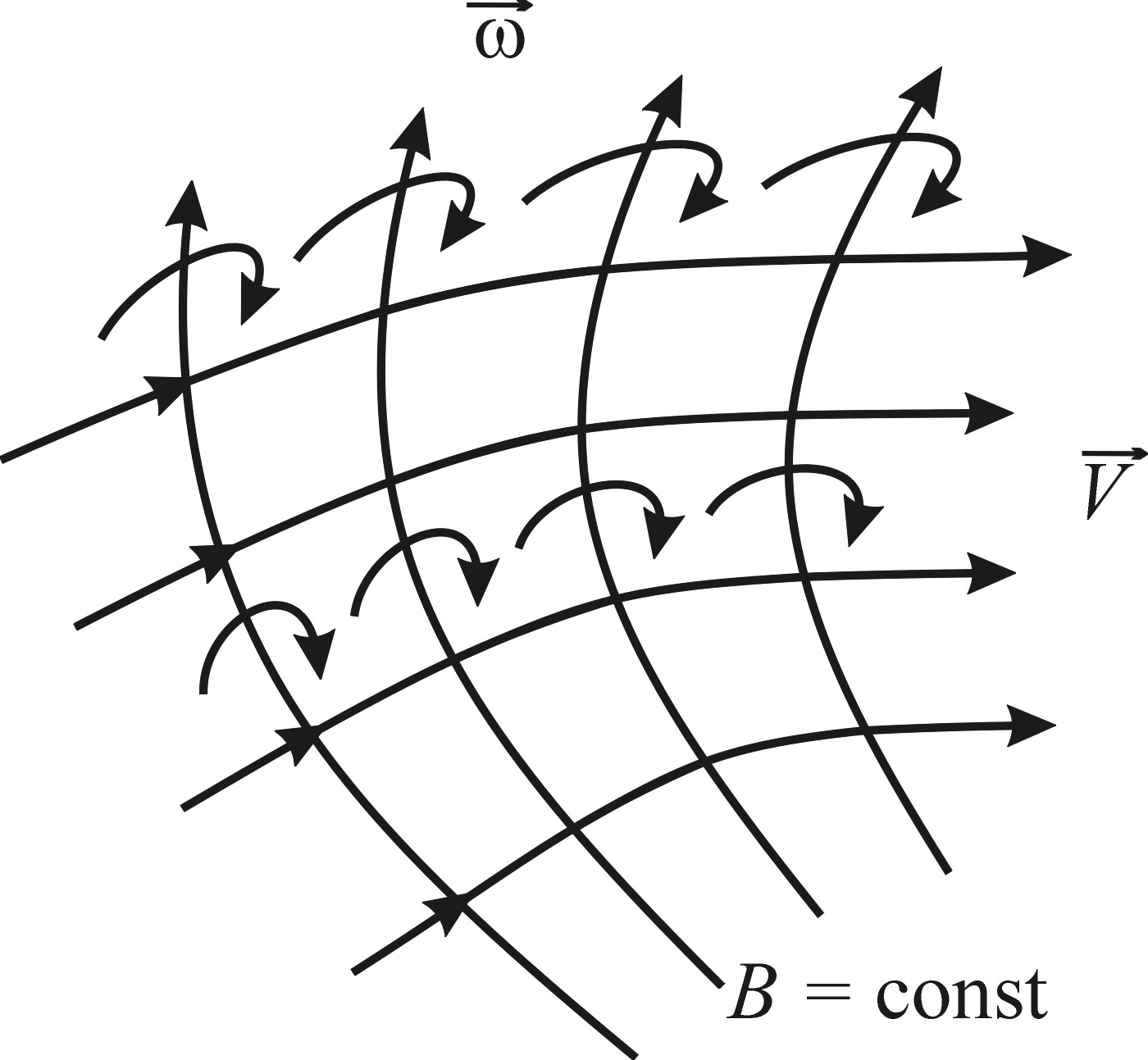

(5.68)

или эти поверхности являются энергетическими поверхностями.

Интеграл Коши  Лагранжа. Пусть , т. е. (в силу теоремы Стокса). Учтем также, что (дифференцирование по независимым переменным и можно поменять местами для непрерывной ). Тогда (5.60) принимает вид

, (5.69)

то есть

. (5.70)

Причем одна и та же для всех геометрических точек всего или той части пространства , которое заполнено жидкостью или газом.

Интеграл Эйлера. Имеем ; и течение стационарно – . В этом случае

. (5.71)