5.3. Уравнения Эйлера движения невязкой жидкости
Движение жидкости подчиняется законам Ньютона и на их основе описывается системой, состоящей из уравнений количества и момента количества движения.
Предположим, что на движущуюся жидкость
действуют объемные силы
.
Общие уравнения движения невязкой
жидкости могут быть получены из
дифференциальных уравнений равновесия
(3.6), если, согласно принципу Д’ аламбера,
к действующим силам добавить силы
инерции. Тогда уравнение движения
запишем так:
. (5.19)
Здесь
– силы инерции, отнесенные к единице
массы и объема. В проекции на оси
декартовых прямоугольных координат
уравнение Эйлера примет вид
(5.20)
Сделав предположение об идеальности жидкости (невязкости, т. е. об отсутствии в жидкости касательных напряжений трения) и добавив к (5.20) уравнение несжимаемости (5.18), получим замкнутую систему уравнений динамики Эйлера.
Для решения определенной задачи
необходимо задаться начальными и
граничными условиями. Начальными
условиями будут:
при t = t0.
Если движение стационарное (установившееся),
начальные условия опускаются.
Граничные условия:
1) условие непроницаемости твердых границ потока, т. е. нормальная составляющая скорости к поверхности канала (трубы, русла и т. п.) во всех его точках должна быть равна нулю; касательная составляющая произвольна. В случае вязкой жидкости это условие заменяется условием «прилипаемости» жидкости к стенкам канала, т. е. условием равенства скоростей жидкости и точек твердой поверхности, по которой она движется.
Условие непроницаемости является общим для задач как внешнего обтекания тел (обтекание лопасти турбины или рабочего колеса насоса, любого тела, движущегося в жидкости и т. п.), так и внутреннего (задач, связанных с течением жидкости в проточной части гидромашин, в трубках, реках и т. д.);
2) задание поля скоростей вдалеке (на бесконечности) от обтекаемого тела (в случае внешнего обтекания) и секундного объемного расхода жидкости сквозь любое сечение канала (внутреннее обтекание).
В рассмотренной общей постановке задач динамики невязкой жидкости решение этих уравнений представляет существенные трудности. Во-первых, уравнение динамики Эйлера записываются в частных производных, т. е. это не обыкновенные дифференциальные уравнения, и, во-вторых, эти уравнения нелинейны из-за наличия в них конвективных членов. Решение этих уравнений в большинстве случаев возможно лишь с помощью численных методов.
5.4. Закон импульсов. Уравнения движения в напряжениях
Математическая формулировка закона импульсов была дана И. Ньютоном в трактате «Nature Fhylosofical» (1654 г.) Анализируя кинематические законы Кеплера о движении планет, И. Ньютон обратил внимание, что для всех из них оказывается справедливым условие
. (5.21)
Тем самым он открыл закон всемирного
тяготения, физическая природа которого
до сих пор не ясна. Одновременно он
обобщил законы кинематики и сформулировал
ставшим знаменитым второй закон механики:
.
Применительно к жидкости закон импульсов записывается в форме
, (5.22)
где
,
тензор напряжений
в среде. Используя преобразование
Остроградского
Гаусса, получим
.
Применив формулу Эйлера (5.7), получаем
(5.23)
По уравнению неразрывности (5.12) первый интеграл тождественно равен нулю. Тогда
. (5.24)
Эта интегральная форма закона импульсов МЖГ удобна при вычислении суммарных нагрузок (и главного вектора внешних сил, действующих со стороны жидкости на движущееся в ней тело, см. рис. 5.4).
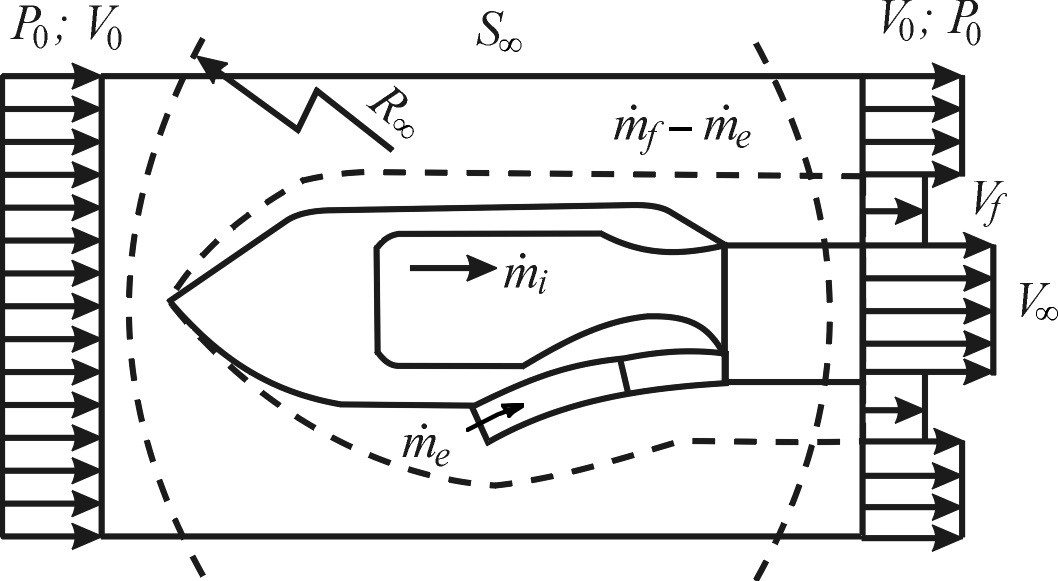
Рисунок 5.4
.
Если
то
.
Стягивая объем
в точку (или опираясь на произвольность
его выбора), получим дифференциальную
форму закона импульсов для МЖГ:
. (5.25)
Его называют в МЖГ уравнением движения в напряжениях. Используя тождественное преобразование Громеки Лэмба:
, (5.26)
ему можно придать форму
. (5.27)
Для ньютоновских жидкостей, т. е. когда
имеется линейная зависимость между
тензором напряжений
и тензором скоростей деформаций
(обобщенный закон Ньютона), получаем
и
. (5.28)
Уравнение движения в напряжениях принимает вид
(5.29)
Обычно пренебрегают изменением
от давления и температуры, т. е. полагают
.
В случае несжимаемых
жидкостей
уравнения движения
(5.30)
были феноменологически получены Навье
и теоретически обоснованы Стоксом.
Поэтому (5.30) называют уравнениями
Навье
Стокса. Для идеальной несжимаемой
жидкости (когда касательными напряжениями
и вязкостью можно пренебречь,
)
будем иметь уравнения, известные еще
Эйлеру:
. (5.31)
В случае баротропной жидкости
в поле консервативных сил
можно ввести функции
и
. (5.32)
Тогда уравнение движения Эйлера (5.31) можно записать в форме Озеена:
(5.33)
или
. (5.34)
Последняя форма более удобна для интегрирования. Векторному уравнению (5.25) всегда соответствуют три скалярных (в проекции на оси координат). Так, для декартовой системы координат будем иметь, например,
, (5.35)
где индексы
и
проходят значения от 1 до 3, причем по
дважды встречающемуся индексу
производится суммирование, т. е.
(5.36)
и аналогично
. (5.37)