5. Динамика невязкой жидкости
Основные уравнения динамики жидкости выводятся на основании общих теорем динамики систем материальных точек. При этом постулируется, что эти общие теоремы, которые в механике доказаны для дискретных материальных точек, справедливы и для сплошной среды.
5.1. Формула Эйлера для дифференцирования по времени интеграла по «живому» объему
В динамике жидкости имеют дело с рядом характерных величин для выделенного произвольного движущегося «живого объема», все время состоящего из одних и тех же частиц:
массой
, (5.1)
импульсом
, (5.2)
моментом импульса
, (5.3)
энергией
, (5.4)
где
внутренняя энергия
среды; с
ее теплоемкость,
.
Общие законы сохранения материи в физике формулируются через ее изменение во времени. Поэтому, по Эйлеру, при движении материальной среды необходимо вычислить
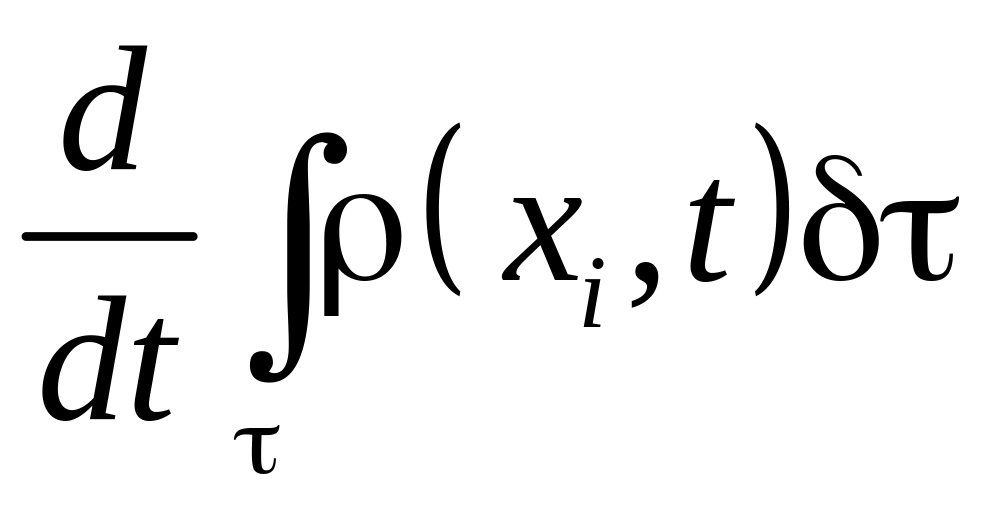(5.5)
следующим образом (см. рис. 5.1):
(5.6)
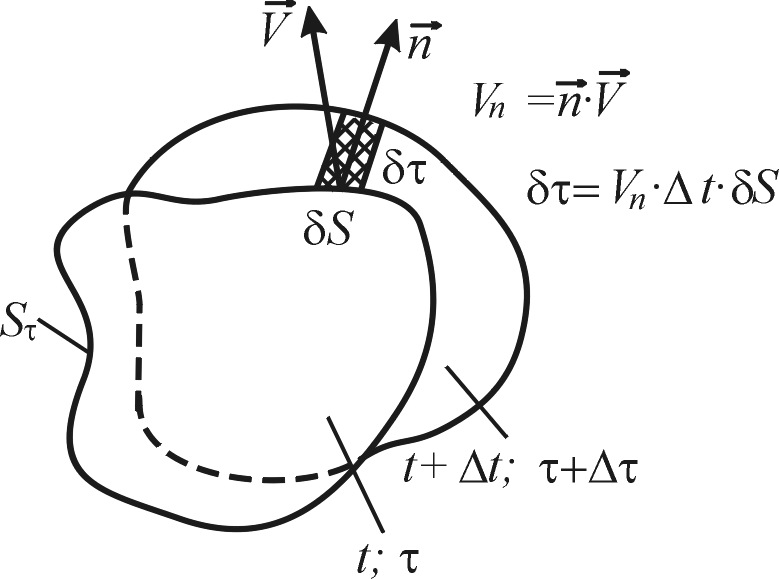
Рисунок 5.1
В последнем пределе учтем, что
и применим к интегралу
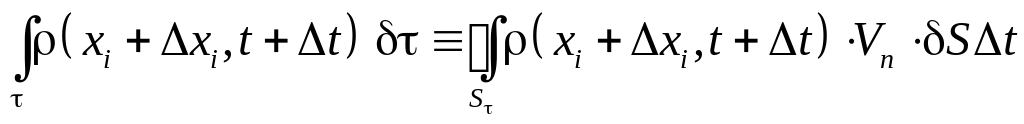
преобразование Остроградского Гаусса, а именно
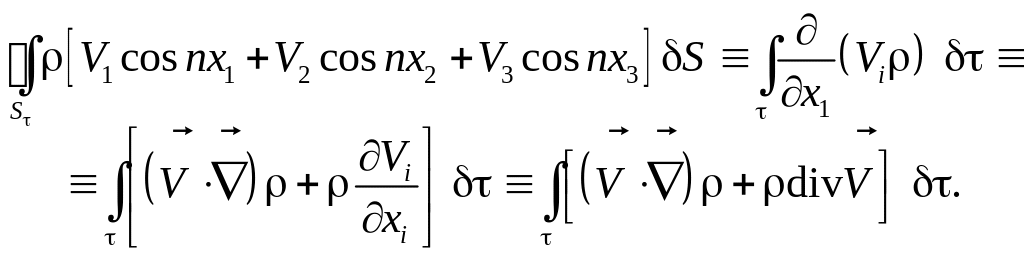
В итоге получаем следующую формулу Эйлера:
(5.7)
при этом имеем формулу Эйлера для разложения полной производной на локальную и конвективную составляющие
Здесь символ
записывается для декартовой системы
координат в форме
(5.8)
Например,
конвективную производную от плотности
можно записывать так:
(5.9)
5.2. Закон сохранения массы. Уравнение неразрывности
Законы сохранения, являющиеся краеугольным камнем современной физики, были впервые сформулированы еще М. В. Ломоносовым, который писал: «… если что-либо исчезает, то в другом месте прибывает».
Конкретное содержание этого фундаментального закона сохранения материи (вещества) на основе химических опытов было дано в 1785 г. А. Лавуазье и Ж. Менье, которые, в частности, получили широко известную теперь формулу для воды
.
В механике жидкости и газа закон сохранения массы представляется следующим образом:
. (5.10)
Применяя формулу Эйлера (5.7), получаем
. (5.11)
В силу произвольности выделенного «живого» объема это может быть тогда и только тогда, когда
. (5.12)
Это и есть
уравнение неразрывности для сплошных
сред (континуумов). С учетом того, что
–
скаляр,
.
Применив формулу
получим уравнение неразрывности в виде
. (5.13)
В случае стационарного
поля плотности (локальная производная
)
(5.14)
В частном случае несжимаемой жидкости
(
)
уравнение (5.14) называется уравнением
несжимаемости:
(5.15)
Для несжимаемых жидкостей
, (5.16)
т. е.
. (5.17)
Расписав (5.12) в проекциях, получим выражение для практических вычислений:
(5.18)
Учитывая, что
,
можно (5.12) придать более компактную
форму:
. (5.18a)
Рисунок
5.2
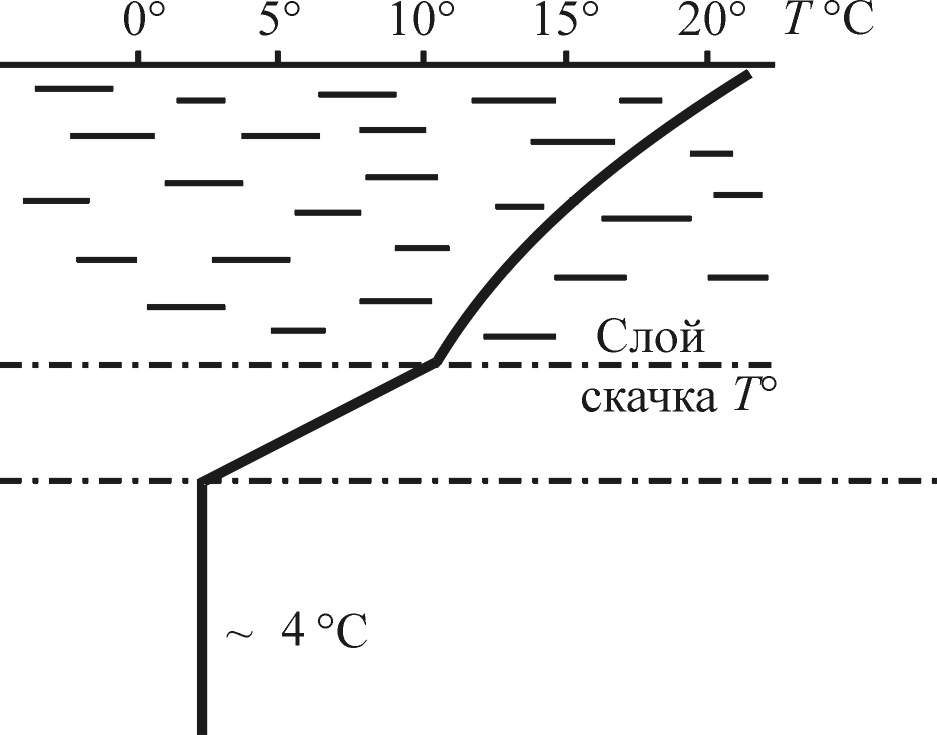
Для морской воды (рис. 5.2) или воды в
прудах-охладителях ТЭС и АЗС с изменением
температуры
плотность
также будет функцией
,
но ее распределение в пространстве
должно подчиняться закону (5.17). Для
сжимаемых жидкостей (например газа,
воздуха)
и должен всегда соблюдаться закон
(5.18a). Если же
плотность – физическая константа (в
большинстве случаев для капельных
жидкостей, в том числе и для воды):
,
то
.
Тогда уравнение неразрывности вырождается в более простое:
,
каковым
и следует
пользоваться для несжимаемых жидкостей
(как капельных, так и газообразных
при малых давлениях и числах Маха
).
Исходя из условия неразрывности движущейся материальной среды следует считать, что, если среда несжимаема, дивергенция вектора скорости должна быть равна нулю в любой точке пространства, занятого потоком. Это положение можно рассматривать и в ином (обратном) смысле, т. е. равенство нулю дивергенции вектора скорости считать признаком несжимаемой движущейся сплошной материальной среды. Этим определяется и принципиальная возможность оценивать дивергенцией вектора скорости объемные деформации в движущейся сплошной материальной среде, что используется при определении нормальных напряжений.
Рассмотрим, как записываются в конкретных случаях уравнения неразрывности.
П
Рисунок
5.3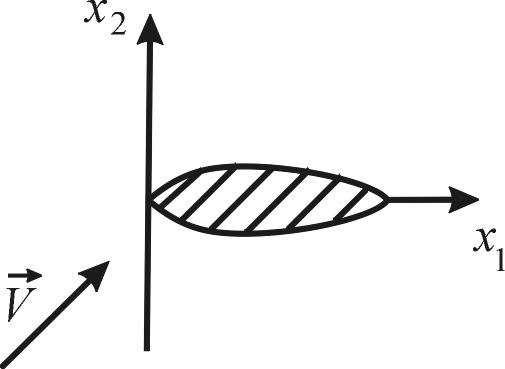
Для установившихся течений параметры жидкости являются функциями только координат точек, следовательно, частные производные параметров по времени обращаются в нуль. А для плоских установившихся течений сжимаемой жидкости около профиля крыла уравнение неразрывности записывается в виде
.