§ 11.10. Анализ деформированного состояния
Рис.11.7 |
Тензор
деформации
|
.
(1.4) представим в симметричном виде
(рис.11.7), когда
и т.д. Анализ деформи-рованного состояния
проведем по аналогии с вышеприведенным
анализом
напряженного
состояния. Три взаимно ортогональных
направления, сдвиги между которыми при
деформации тела равны нулю, называются
главными
осями деформированного
состояния. Линейные деформации по этим
направлениям называются главными
деформациями
и обозначаются
.
Главные деформации находятся из уравнения, аналогичного уравнению (11.5) для определения главных напряжений
. (11.17)
Здесь
и
инварианты деформированного состояния:
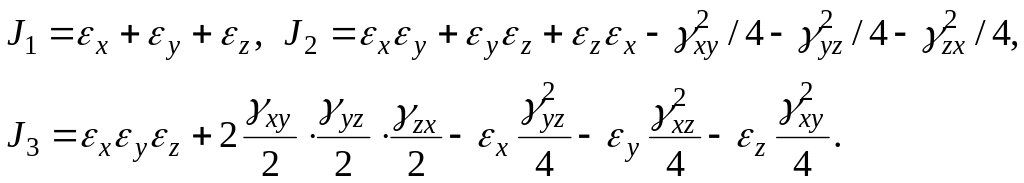(11.18)
Решение кубического
уравнения (11.17) дает три величины главных
деформаций
.
В случае плоской
деформации, когда, например,
по аналогии с ПНС формулы (11.12), получим
и
:
. (11.19)
Экстремальные сдвиги находятся по формулам, аналогичным (11.7), для определения экстремальных касательных напряжений:
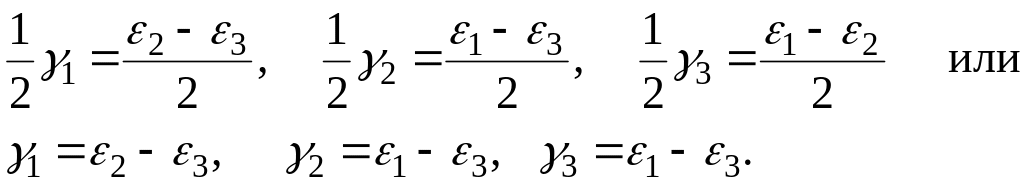(11.20)
Для изотропных материалов направления главных деформаций совпадают с направлениями главных напряжений.
Выясним физический
смысл инварианта
:
Рассмотрим кубик, у которого ребра
совпадают с направлениями главных
деформаций и до нагружения тела их длины
равны 1. Его объем
.
После деформации его объем станет
.
Относительное
изменение объема обозначим
:
,
.
Деформации малы, поэтому величины второго и третьего порядка малости можно не учитывать, тогда
.
(11.21)
Итак, первый инвариант деформированного состояния определяет относительное изменение объема тела.
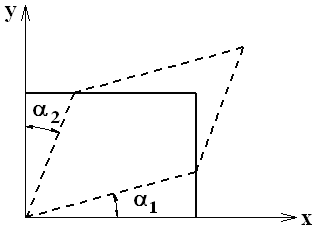
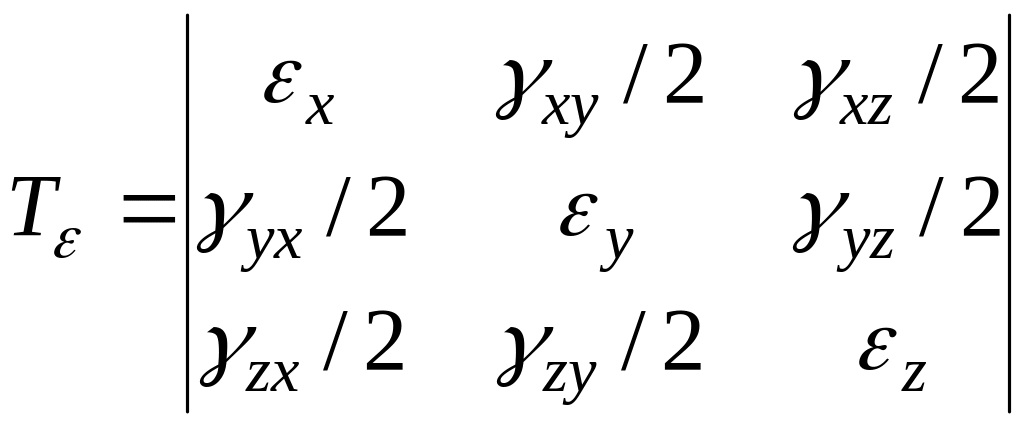