- •Раздел 11
- •Часть I. Объемное напряженное состояние
- •§ 11.1. Напряжения на наклонных площадках
- •§ 11.2. Полное, нормальное и касательное напряжения на
- •§ 11.3. Главные напряжения, главные площадки
- •§ 11.4. Экстремальные касательные напряжения
- •§ 11.5. Октаэдрические нормальные и касательные
- •Часть II. Плоское напряженное состояние
- •§ 11.6. Полное, нормальное и касательное напряжения на
- •§ 11.7. Главные напряжения, главные площадки
- •§ 11.8. Экстремальные касательные напряжения
- •§ 11.9. Чистый сдвиг
- •§ 11.10. Анализ деформированного состояния
§ 11.7. Главные напряжения, главные площадки
Здесь, как и в
объемном напряженном состоянии, имеются
главные
площадки с
направляющими косинусами
![]() и
и
![]() ,
на которых нормальные напряжения
экстремальны, и они называются главными
напряжениями
,
а касательные напряжения отсутствуют.
Поэтому здесь
,
на которых нормальные напряжения
экстремальны, и они называются главными
напряжениями
,
а касательные напряжения отсутствуют.
Поэтому здесь
![]()
![]() .
Подставляя это в формулы (11.9), получим:
.
Подставляя это в формулы (11.9), получим:
![]() (16)
(16)
Известно, что
![]() ,
поэтому уравнения (16) имеют решение,
если его определитель
,
поэтому уравнения (16) имеют решение,
если его определитель
![]() .
.
Раскроем этот определитель
![]() . (17)
. (17)
Здесь
![]() инварианты
ПНС.
инварианты
ПНС.
Решение квадратного уравнения (17) дает два корня и , которые и называют главными напряжениями в ПНС:
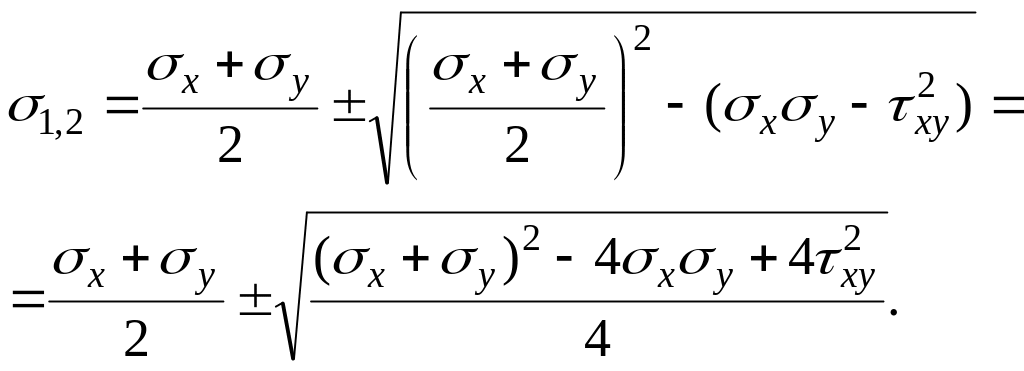
Окончательно получим для (знак (+)) и (знак (–)):
![]() .
(11.12)
.
(11.12)
Положение главных
площадок,
где действуют
и
,
в ПНС удобно определять углами
![]() ,
которые нормали к главным площадкам
составляют с осью
.
Их легко определить из условия отсутствия
на главных площадках касательных
напряжений. Подставляя
,
которые нормали к главным площадкам
составляют с осью
.
Их легко определить из условия отсутствия
на главных площадках касательных
напряжений. Подставляя
![]() и
и
![]() в (11.11), получим
в (11.11), получим
![]() ,
,
откуда
![]() . (11.13)
. (11.13)
Из (11.13) получим
два значения
,
одно
,
другое
![]() ,
которые определяют две взаимно
ортогональные главные площадки.
,
которые определяют две взаимно
ортогональные главные площадки.
![]() и
и
![]() откладывать от оси
против хода часовой стрелки.
откладывать от оси
против хода часовой стрелки.
Чтобы не выяснять,
на каких площадках действуют
и
,
надо подставить
и
![]() в формулу (11.10), большая величина
в формулу (11.10), большая величина
![]() ,
а меньшая
,
а меньшая
![]() .
Эти величины
и
должны быть равны величинам, вычисленным
по (11.12).
.
Эти величины
и
должны быть равны величинам, вычисленным
по (11.12).
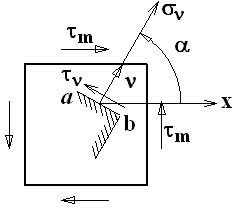
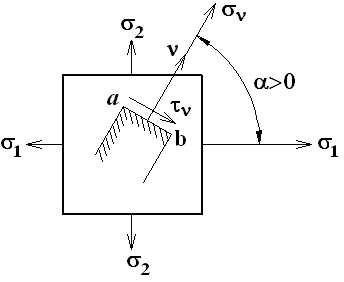
§ 11.8. Экстремальные касательные напряжения
Вырежем из тела,
испытывающего ПНС, прямоугольный элемент
с главными площадками, на которых
действуют
и
(рис.11.5). Выделим наклонную площадку ab,
нормаль
к которой с направлением
составляет угол
![]() .
Напряжения
и
.
Напряжения
и
![]() на этой площадке найдем по зависимостям
(11.10) и (11.11), полагая
на этой площадке найдем по зависимостям
(11.10) и (11.11), полагая
![]() .
.
Рис.11.5 |
Из второй формулы
(18) видно, что при
Подставляя сюда и из формулы (11.12), получим
|
Итак, экстремальные касательные напряжения действуют на площадках под углом 45 к главным и определяются по формулам (11.14) или (11.15).
Нормальные
напряжения
![]() на этих площадках найдем по первой
формуле (18), подставляя
(
на этих площадках найдем по первой
формуле (18), подставляя
(![]() ):
):
![]() . (19)
. (19)
Здесь учтено, что
![]() .
.
§ 11.9. Чистый сдвиг
Рассмотрим частный
случай ПНС, когда главные напряжения
![]() .
.
В этом случае
экстремальные
![]() найдем по (11.14), а нормальные напряжения
найдем по (11.14), а нормальные напряжения
![]() на этих площадках по (19). Итак
на этих площадках по (19). Итак
![]() .
.
Такой случай носит название чистый сдвиг.
Рис. 11.6 |
Вырежем из тела
прямоугольный элемент, испытывающий
чистый сдвиг, т.е. по его граням действуют
только
(рис.11.6). Найдем нормальное напряжение
и касательное
на наклонной площадке
под углом
|
Из этих формул
видно, что при
![]() ,
а это, как известно, характеристики
главной площадки.
,
а это, как известно, характеристики
главной площадки.
Итак, при чистом сдвиге главные площадки расположены под углом 45 к площадкам чистого сдвига, а главные напряжения на них:
![]() (при
(при
![]() ).
).

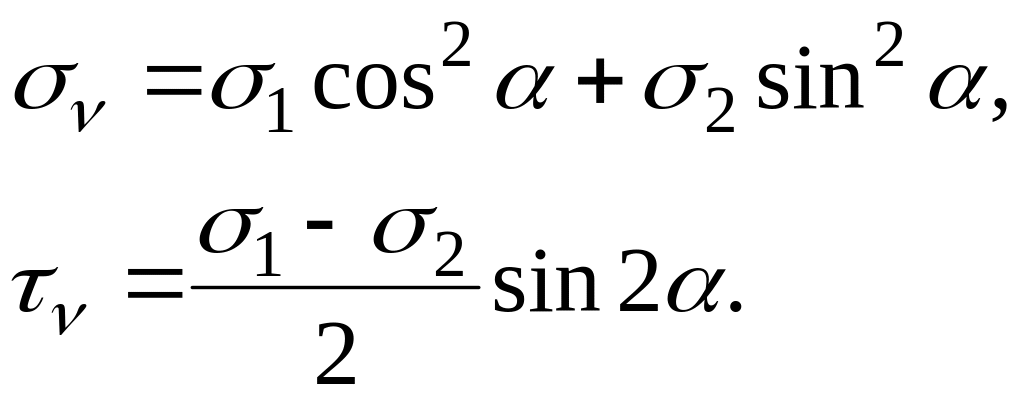 (18)
(18)