Раздел 11

анализ напряженно-деформированного

состояния в точке тела

Часть I. Объемное напряженное состояние

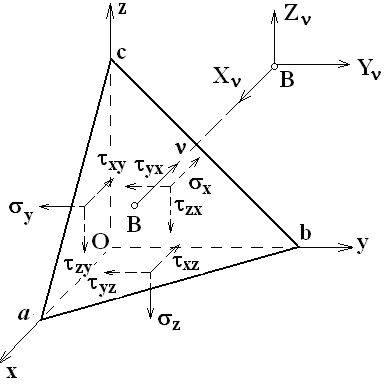
§ 11.1. Напряжения на наклонных площадках

(Условия на поверхности)

Рис.11.1

Вырежем из нагруженного тела бесконечно малый тетраэдр с тремя плоскостями, совпадающими с координатными (см. рис. 11.1). Положение в пространстве наклонной пло-щадки определяется нор-малью , направляющие конусы которой обозначим так: Площадку обозначим . Невидимые треугольные пло-щадки, перпендикулярные осям и , обозначим и

определим так:

. (1)

На этих невидимых, отрицательных площадках, действуют положительные напряжения, определяемые . На наклонной площадке действуют компоненты полного напряжения и . Под действием всех напряжений, показанных на рис.11.1, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики

. (2)

Объемные силы и здесь не учитываются, т.к. они пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (2) – второй порядок малости. Подставляя (1) в (2) и сокращая на , получим

. (3)

Составляя уравнения статики и , получим еще два уравнения, которые легко записать, используя кольцевую перестановку и , получим три уравнения равновесия тетраэдра:

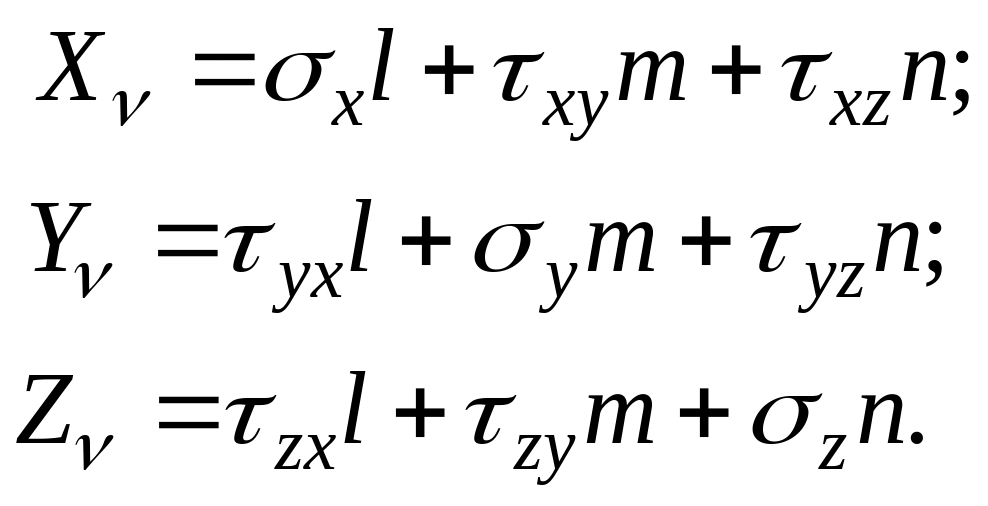(11.1)

Если площадка совпадает с поверхностью тела, то и соответствуют компонентам внешней нагрузки. В этом случае уравнения (11.1) называют условиями на поверхности тела. Они связывают внешние напряжения с внутренними в теле.

§ 11.2. Полное, нормальное и касательное напряжения на

наклонной площадке

На рис. 11.1 показаны компоненты полного напряжения на наклонной площадке . Очевидно, что его численное значение определяется так:

.

Подставляя сюда формулы (11.1), найдем

. (11.2)

Полное напряжение можно разложить на нормальное и касательное напряжения на наклонной площадке. Очевидно, что . Напряжение можно найти, проектируя и на нормаль , т.е. . С учетом формул (11.1) получим

. (11.3)

Касательное напряжение можно найти так:

. (11.4)

§ 11.3. Главные напряжения, главные площадки

На наклонной площадке, у которой орт нормали совпадает с направлением , величина , а будет экстремально и равно . Такая площадка называется главной (ее направление определяют направляющие косинусы, которые обозначим ). А напряжения на ней обозначим . Все его проекции на оси будут . Подставим их в формулы (11.1):

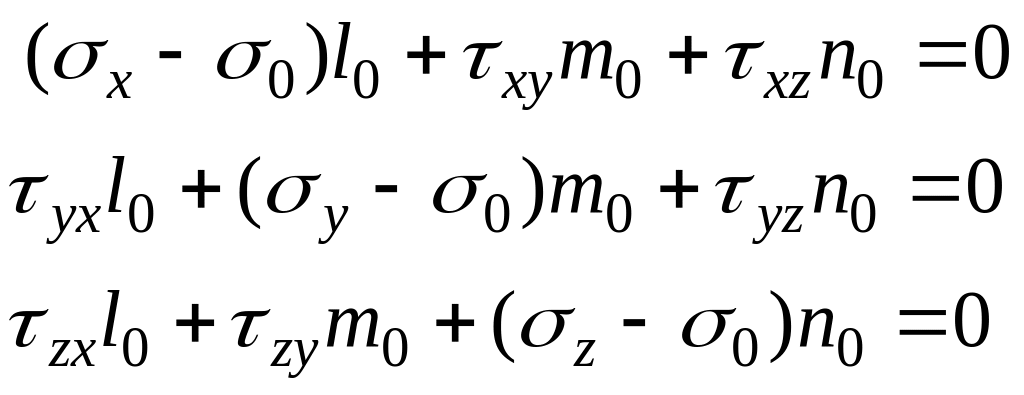или (4)

Надо найти и при известных напряжениях в точке тела .

Очевидно, что

. (5)

Из этого следует, что одновременно не могут быть равны нулю. Тогда система уравнений (4) имеет решение, если ее определитель

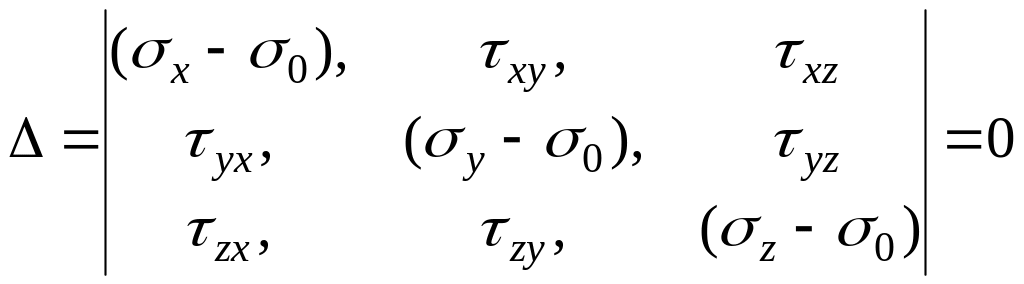. (6)

Раскрывая этот определитель, получим, с учетом закона парности касательных напряжений:

(7)

(8)

После перемножений и приведения подобных членов найдем

. (11.5)

Где:

. (11.6)

Величины и называются инвариантами тензора напряжений (легко убедится, что есть определитель ). При повороте осей компоненты меняются, но и при этом не должны меняться, т.к. , определяемые из (11.5), не зависят от выбора положения осей , а зависят от нагружения тела.

Решение кубического уравнения (11.5) дает три корня для , которые и называются главными напряжениями. Итак, имеем три главных напряжения, которые действуют на трех главных площадках, определяемых . Например, найдем главной площадки, где действует . Для этого составим три уравнения: и любые два уравнения из системы (4), подставляя в них . Решая эти три уравнения, найдем . Аналогично определяются две другие площадки, где действуют и . Можно показать, что главные площадки взаимно ортогональны.

Инварианты напряженного состояния через главные напряжения определяются с учетом (11.6) так:

Здесь учтено, что на главных площадках нет касательных напряжений.