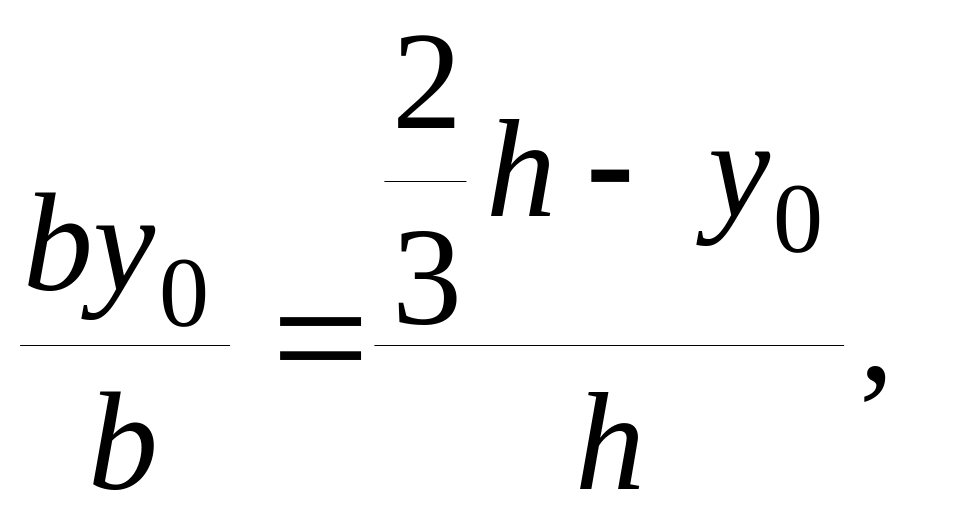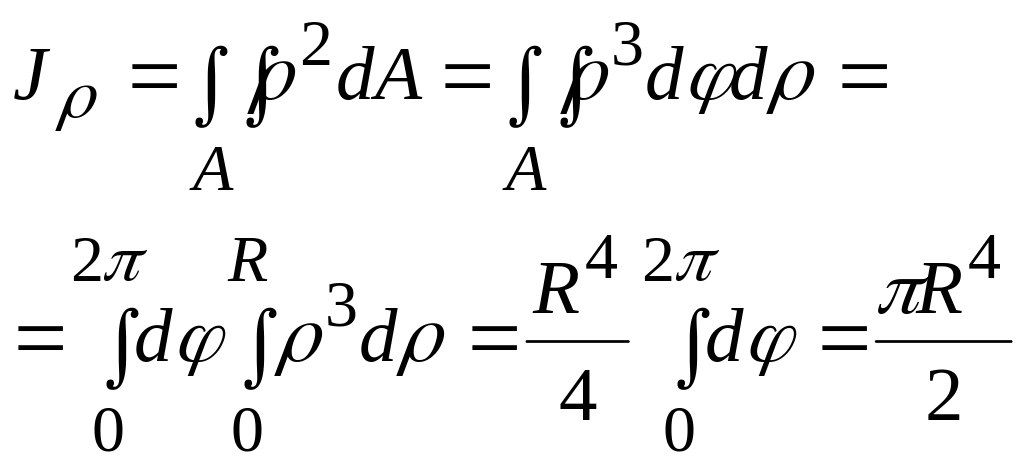§ 2.5. Эллипс инерции

Введем новую геометрическую характеристику, которую назовем радиусом инерции.

. (2.15)

Предположим, что для какой-либо фигуры оси и являются главными центральными осями. Запишем выражение момента инерции относительно оси , наклонной к оси на угол . На основании (2.11) получим

, т.к. .

Разделив все на А, получим

. (2.16)

Рис. 2.8

Построим в осях эллипс, взяв за полуоси радиусы инерции фигуры (рис. 2.8). При этом вдоль оси отложим радиус , а на оси - радиус .

Данный эллипс называ-ется эллипсом инерции.

Проведем касательную к эллипсу, параллельную оси . Можно показать, что расстояние между касатель-ной и осью , обозначенное

на рис. 2.8 величиной h, равно:

. (2.17)

Сравнивая полученную зависимость с выражением (2.16), видим, что величина численно равна радиусу инерции относительно наклонной оси . Установленное свойство эллипса инерции позволяет графически определить момент инерции относительно любой оси, проходящей через начало координат. Для этого достаточно провести касательную к эллипсу параллельно этой оси и замерить кратчайшее расстояние между касательной и осью. Это расстояние будет равно радиусу инерции для рассматриваемой оси. Момент инерции определяется так: