Выполняется, и это означает, что коэффициент корреляции значим (имеет место зависимость между параметрами х и у).

2. Вычисление средней ошибки коэффициента корреляции

При r/m_r ³ 3 коэффициент корреляции считается достоверным, т.е. связь доказана. При r/m_r < 3 связь недостоверна.

Для рассматриваемого примера , r/m_r = 0,51/0,148 = 3,446 > 3 – связь достоверна.

3. Метод сравнения контрольных карт медиан

Простым методом анализа степени корреляционной зависимости считается метод медиан (метод сравнения графиков), удобный при исследовании технологического процесса с использованием данных, полученных на рабочем месте.

Пусть величины х и у заданы с помощью графиков или контрольных карт, причем количество измерений для параметров х и у должно быть одинаково. Проводятся линии медиан Me_x, Me_y. Точкам выше медиан присваивается символ «+», точкам ниже медиан -  символ «-», точкам, находящимся на медиане - символ «0».

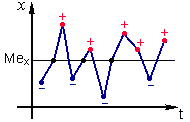
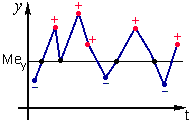
Рис. 17

Каждой паре значений (x,y) соответствует пара символов.  Пары символов заменяются одним кодом по правилам: 

Пара	Код
+ +	+
– –	+
+ – (– +)	–
+ 0	0
– 0	0
0 0	+

Далее следует подсчитать:

- число кодов "+" - N(+),  - число кодов "–"  - N(–),  - число кодов "0" - N(0),

- число k = N(+) + N(-).

Затем нужно вычислить два числа P = N(+) + N(0)/2 и M = N(–) + N(0)/2 и найти наименьшее из них min(Р, М). По таблице кодовых значений для известного значения k и заданном коэффициенте риска α = 1 – Р (Р - доверительная вероятность) следует найти соответствующее минимальное значение min_k. Если min(Р, М) ≤ min_k, то корреляционная зависимость существует, причем:

 при P > M - положительная (прямая) корреляция;  при P < M – отрицательная (обратная) корреляция

Применим этот метод для рассматриваемого нами примера:

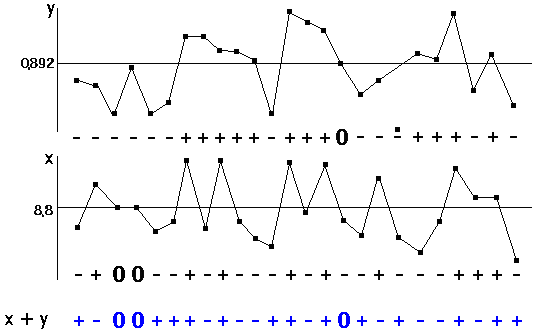
Рис. 18

Подсчитываем числа кодов:

Р = N(+) + N(0)/2 = 13 + 3/2 = 14,5;

М = N(–) + N(0)/2 = 9 + 3/2 = 10,5;

k = 13 + 9 = 22.

Из двух значений Р и М выбирается меньшее (10,5) и сравнивается с кодовым значением из таблицы 4, соответствующим значению k. По таблице 4 находим, что кодовое число, соответствующее k = 22, при коэффициенте риска 0,05 равно 5. Поскольку min (Р, М) = 10,5 > 5, можно сделать заключение о том, что корреляция отсутствует, т.е. нельзя говорить о корреляционной зависимости между давлением сжатого воздуха и процентом дефектов в процессе литья под давлением тонкостенных деталей.

Таблица 4 - Таблица кодовых значений 

k	α		k	α		k	α
	0,01	0,05		0.01	0.05		0.01	0.05
8	0	0	36	9	11	64	21	23
9	0	1	37	10	12	65	21	24
10	0	1	38	10	12	66	22	24
11	0	1	39	11	12	67	22	25
12	1	2	40	11	13	68	22	25
13	1	2	41	11	13	69	23	25
14	1	2	42	12	14	70	23	26
15	2	3	43	12	14	71	24	26
16	2	3	44	13	15	72	24	27
17	2	4	45	13	15	73	25	27
18	3	4	46	13	15	74	25	28
19	3	4	47	14	16	75	25	28
20	3	5	48	14	16	76	26	28
21	4	5	49	15	17	77	26	29
22	4	5	50	15	17	78	27	29
23	4	6	51	15	17	79	27	30
24	5	6	52	16	18	80	28	30
25	5	7	53	16	18	81	28	31
26	6	7	54	17	19	82	28	31
27	6	7	55	17	19	83	29	32
28	6	8	56	17	20	84	29	32
29	7	8	57	18	20	85	30	32
30	7	9	58	18	21	86	30	33
31	7	9	59	19	21	87	31	33
32	8	9	60	19	21	88	31	34
33	8	10	61	20	22	89	31	34
34	9	10	62	20	22	90	32	35
35	9	11	63	20	23	91	32	35

4. Метод медиан на диаграмме разброса

Другой метод анализа оценки значимости корреляционной зависимости основан на проведении на диаграмме разброса вертикальной и горизонтальной прямых линий, соответствующих медианным значениям переменных х и у.  Выше и ниже горизонтальной прямой, справа и слева от вертикальной прямой должно быть равное число точек. Если общее число точек окажется нечетным, медианы следует провести через центральную точку (в приведенном примере на рисунке 19 вертикальная и горизонтальная медианы пройдут через 13-ю точку ранжированного ряда, так как число точек равно 25).

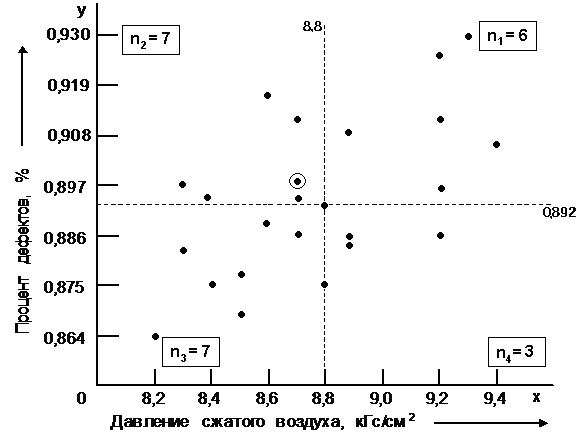
 Рисунок 19 – Диаграмма рассеяния для давления сжатого воздуха  и процента дефектов

В каждом из четырех квадрантов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают n₁,  n₂,  n₃,  n₄  соответственно. Точки, через которые прошла медиана не учитывают. Отдельно складывают точки в положительных (1-ый и 3-ий) и отрицательных (2-ой и 4-ый) квадрантах.

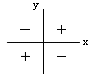
Положительные и отрицательные квадранты рассматриваются относительно проведенных на диаграмме разброса медиан.

n ₍₊₎ = n₁ + n₃

n _(-) = n₂ + n₄ 

k = n ₍₊₎ + n _(-)

Для рассматриваемого примера:

n ₍₊₎ = 6 +7 = 13

n _(-) =7 + 3 = 10

k =13 + 10 = 23

Так как две точки находятся на медиане, то k не равно 25.

 

Для определения наличия и степени корреляции по методу медиан также используется таблица кодовых значений (таблица 4), соответствующих различным значениям k при двух значениях коэффициента риска α (0,01 и 0,05).

Из n₍₊₎ и n_(-)  выбирается меньшее значение и сравнивается с кодовым значением из таблицы 4. Делают заключение о наличии или отсутствии корреляции. Если меньшее из чисел n оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место. В случае, когда n(+) > n(-),  то это свидетельствует о прямой корреляции, в противном случае, когда  n(+) < n(-), можно говорить об обратной корреляции. В рассматриваемом примере табличное кодовое значение при коэффициенте риска α = 0,05, соответствующее k = 23, равно 6. Поскольку n ₍₊₎ = 13, n_(-) = 10, то меньшим из чисел будет  n_(-) = 10, а 10 > 6, можно утверждать, что в данном случае между двумя параметрами не наблюдается корреляционной зависимости, т.е. нельзя говорить о корреляционной зависимости между давлением сжатого воздуха и процентом дефектов в процессе литья под давлением тонкостенных деталей.

Исходя из различных способов выявления наличия корреляционной зависимости, получаем, что расчетный коэффициент корреляции является значимым и значит, корреляционная зависимость существует. Однако изучение диаграммы по методу медиан и методу сравнения соответствующих графиков показывает, что явной корреляционной зависимости не наблюдается. Поэтому, проведя один анализ, или рассматривая диаграмму рассеяния однобоко, нельзя однозначно сказать о наличии корреляционной зависимости или о ее характере (прямая, обратная и т.д.), а если такое заключение делается, то оно требует либо проверки экспериментом, либо проведения дополнительного исследования.

Иногда случайно проявляется сильная корреляция, которая не подкрепляется вовсе, или подкрепляется слишком слабой причинно-следственной зависимостью между ними. Корреляция такого рода называется ложной корреляцией. Даже если коэффициент корреляции высок, это совсем не обязательно указывает на причинно-следственную связь.

Порядок выполнения работы.

1. Ознакомиться с общими положениями.

2. Рассмотреть приведенный пример.

3. В соответствии с указанным преподавателем заданием (Приложение А)

построить диаграмму разброса, произвести ее анализ и расчет тесноты связи между параметрами.

4. По результатам проделанной работы сделать выводы.

Требования к отчету.

Отчет по работе должен содержать:

- тему и цель работы;

- вариант задания;

- диаграмму разброса

- анализ диаграммы разброса и расчет степени связи между параметрами,

- выводы.