Анализ характера изменения параметров качества во времени

Диаграмма разброса позволяет наглядно показать характер изменения параметра качества во времени. Для этого из начала координат проводится биссектриса. Если все точки будут находиться на биссектрисе, то это означает, что значения данного параметра не изменились в процессе эксперимента. Следовательно, рассматриваемый фактор (или факторы) не влияет на параметр качества. Если основная масса точек лежит под биссектрисой, то это значит, что значения параметров качества за прошедшее время уменьшилось. Если же точки ложатся выше биссектрисы, то значения параметра за рассматриваемое время возросли. Проведя лучи из начала координат, соответствующие уменьшению увеличению параметра на 10, 20, 30, 50 %, можно путем подсчета точек между прямыми выяснить частоту значений параметра в интервалах 0…: %, 10…20 % и т.д.

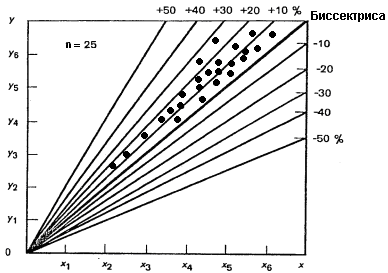
Рис. 16 Пример анализа диаграммы разброса.

Определение тесноты связи между исследуемыми параметрами.

Существуют различные способы количественной оценки степени корреляционной зависимости. Один из них основан на вычислении коэффициента корреляции r.  Коэффициент корреляции определяет меру линейной зависимости между случайными величинами, его величина рассчитывается по формуле:

где    х_i и у_i – значения параметров х и у для i-го измерения;

          и - средние арифметические величин х и у, которые определяются по формулам:

                            = (х₁ + х₂ + х₃ +...+ х_n) / n,                                 (1)

                           = (у₁ + у₂ + у₃ +…+ у_n) / n,                                  (2)

где    n – объем выборки, т.е. количество измерений;

S_х и S_у – средние квадратические (стандартные) отклонения величин х и у.

С учетом формул для средних квадратических отклонений

и ,

получаем

.

                      

Величина коэффициента корреляции может изменяться в пределах

,

Причем считается, если между величинами x и y

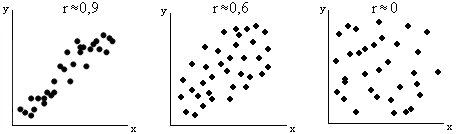
- имеется сильная положительная (прямая) корреляция, то r ≈ +1;

- имеется сильная отрицательная (обратная) корреляция, то r ≈ –1;

- имеется слабая корреляция, то │r │≈ 0,4 – 0,6;

- нет корреляции, то r = 0.

Определим коэффициент корреляции для рассматриваемого примера изготовления деталей с тонкими стенками. Значения ∆х = х_i -   и ∆у = у_i - , S_х и S_у приведены в таблице 2.

Таблица 2 – Расчетная таблица для данных о давлении сжатого воздуха и проценте дефектов в процессе литья под давлением 

Дата	Давление, кГс/см2, х	Процент дефектов, у	∆х= хi -	∆у= уi -	Δх ∙ ∆у	(Δх)2	(Δу)2
1	8,6	0,889	-0,169	-0,00384	0,0006489	0,0286	0,0000147
2	8,9	0,884	0,136	-0,00884	-0,0012022	0,0185	0,0000781
3	8,8	0,874	0,036	-0,00384	-0,0006782	0,0013	0,0003549
4	8,8	0,891	0,036	-0,00184	0,0000662	0,0013	0,0000033
5	8,4	0,874	-0,364	-0,01884	0,0068577	0,1325	0,0003549
8	8,7	0,886	-0,064	-0,00684	0,0004377	0,0041	0,0000467
9	9,2	0,911	0,436	0,01816	0,0079177	0,1901	0,0003300
10	8,6	0,912	-0,169	0,01916	0,0032380	0,0280	0,0003670
11	9,2	0,895	0,436	0,00216	0,0009417	0,1901	0,0000046
12	8,7	0,896	-0,064	0,00316	-0,0002022	0,0041	0,0000099
15	8,4	0,894	-0,364	0,00116	-0,0004222	0,1325	0,0000013
16	8,2	0,864	-0,564	-0,02884	0,0162657	0,3181	0,0008317
17	9,2	0,922	0,436	0,02916	0,0127137	0,1901	0,0008503
18	8,7	0,909	-0,064	0,01616	-0,0010342	0,0041	0,0002611
19	9,4	0,905	0,636	0,01216	0,0077337	0,4045	0,0001478
22	8,7	0,892	-0,064	-0,00084	0,0000537	0,0041	0,0000007
23	8,5	0,877	-0,264	-0,01584	0,0041817	0,0697	0,0002509
24	9,2	0,885	0,436	-0,00784	-0,0034182	0,1901	0,0000614
25	8,5	0,866	-0,264	-0,02684	0,0070857	0,0697	0,0007203
26	8,3	0,896	-0,464	0,00316	-0,0014662	0,2151	0,0000099
29	8,7	0,896	-0,064	0,00316	-0,0002022	0,0041	0,0000099
30	9,3	0,928	0,536	0,03516	0,0188457	0,2873	0,0012360
31	8,9	0,886	0,136	-0,00684	-0,0009302	0,0185	0,0000467
1	8,9	0,908	0,136	0,01516	0,0020617	0,0185	0,0002298
2	8,3	0,881	-0,464	-0,01184	0,0054937	0,2151	0,0001401
= 8,7644    = 0,89284                        ΣΔxΔy = 0,078379       Sх = 0,33       Sу = 0,016

При подстановке данных получаем

r =

Значение r равное 0,51 позволяет предположить существование некоторой положительной корреляции между давлением сжатого воздуха и процентом дефектов деталей, изготовляемых методом литья под давлением.

Так как коэффициент корреляции r ≈ 0.5, то необходимо проверить его значимость (существует ли на самом деле корреляция?). Проверить значимость коэффициента корреляции можно несколькими способами.

1. Вычисление расчетной значимости

Расчет значимости коэффициента корреляции производится по формуле

                                   Н_р = |r| ,                                   (3)

где   Н_р – расчетная значимость;

n – объем выборки;

r – коэффициент корреляции.

Затем полученное значение сравнивается с табличной значимостью Н_т, при этом должно выполняться соотношение Н_р ≥ Н_т

 Значения табличной значимости при различных степенях вероятности представлены в таблице 3.

   Таблица 3 - Значения табличной значимости (H_T)

P	n
	10	20	30	40	80	100
0,90	1,65	1,65	1,65	1,65	1,66	1,66
0,95	1,90	1,95	1,95	1,95	1,95	1,96
0,99	2,30	2,45	2,50	2,50	2,55	2,58

 При доверительной вероятности Р = 0,99 и n = 25 по таблице 3 определим Н_т = 2,475. Расчет Н_р по формуле (3) дает следующий результат

Н_р = 0,51 = 2,498

 Таким образом, требуемое условие

Н_р = 2,498 ≥ Нт = 2,475