Практическое занятие № 9.

Тема: Гистограмма.

Цель работы: целью данной работы является закрепление навыков построения и интерпретации гистограмм.

Общие положения.

Гистограммы применяются главным образом для изучения количественных закономерностей производственных или других процессов, при оценивании уровня качества продукции по периодам наблюдений, но могут использоваться и для расчетных значений. Благодаря простоте построений и наглядности гистограммы нашли широкое применение в управлении качеством.

Гистограмма представляет собой столбиковый график, построенный по полученным за определенный период данным, которые разбиваются на несколько интервалов. Число данных, попадающих в каждый из интервалов (частота) выражается высотой столбика. Гистограмма наглядно показывает величину и характер разброса контролируемого параметра. При наложении на гистограмму полей допуска контролируемого параметра можно сделать заключение о стабильности процесса и наличии нескольких влияющих факторов.

При вычерчивании гистограммы совокупность прямоугольников располагают на горизонтальной оси. Основаниями прямоугольников являются интервалы, шириной h, на которые разбивается ряд значений контролируемого параметра, а ординатами -  относительные частоты f_i (или m_i), характеризующие число значений, попавших в каждый интервал.

Для построения гистограммы  нужно число данных не менее 30 - 50, оптимальное число – порядка 100. Если их оказывается более 300, то затраты времени на их обработку оказываются слишком большими.

Построение диаграммы производится в определенной последовательности.

 Рассмотрим построение гистограммы на конкретном примере.

Пример

Для изучения процесса изготовления на токарном станке стальных осей произведены измерения диаметров 90 единиц продукции. Согласно ТУ диаметр оси должен иметь размеры 2,525 ± 0,03 см.

Шаг 1

По результатам измерений составляется таблица исходных данных - таблица 1.

Таблица 1

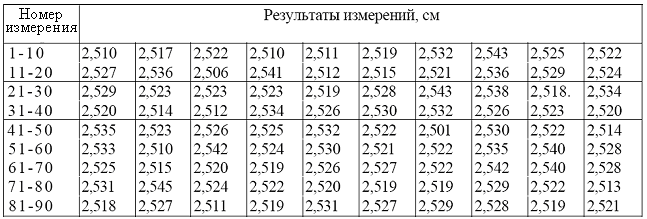
Шаг 2

Весь диапазон изменения (размах R) изучаемой величины разбивается на несколько интервалов. Для этого определяют наибольшее Хmax и наименьшее Хmin  значения для всех данных и находят выборочный размах. При большом числе значений (порядка 100) определение Хmax и Хmin  производят следующим образом: вначале определяют наибольшее и наименьшее значения в каждом десятке значений, а затем среди полученных значений определяют Хmax и Хmin для всего массива данных.

Для рассматриваемого примера составлена Таблица 2.

Таблица 2

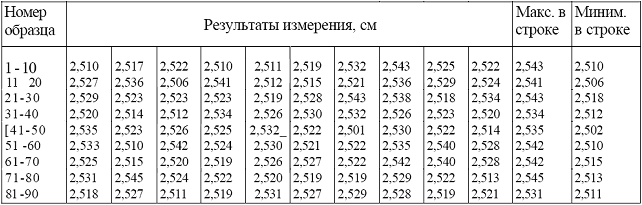
Количество измерений: n = 90

Наибольшее значение - Хmax = 2,545 см

Наименьшее значение - Хmin = 2,502 см

Выборочный размах R = Хmax - Хmin = 2,545 - 2,502 = 0,043 см

Далее, задавшись числом интервалов k (оно должно примерно соответствовать корню квадратному из числа данных n), определяют ширину интервала h. Для этого величину R делят на число интервалов, и полученное число округляют (как правило, в большую сторону).

В приведенном примере:

 k = = ≈ 9 – количество участков;

h = R / k = (2,545 – 2,502) / 9 = 0,043 / 9 ≈ 0,005 см             

Шаг 3

Выбирают границы интервалов. Сначала устанавливается точка отсчета, соответствующая нижней границе первого интервала, при этом первый интервал должен включать в себя наименьшее значение Хmin.  За начало первого интервала рекомендуется брать величину

Хнач = Хmin - точность измерения / 2,

(эта формула не является обязательной и можно из Хmin вычитать и другое значение по своему усмотрению).

В данном случае точность измерения диаметра валов составляет 0,001 см, для нижней границы первого интервала получаем

Хнач = 2,502 – 0,001 / 2 = 2,502 – 0,0005 = 2,5015 см.

Для дальнейших расчетов примем, например, Хнач = 2,5005 см. К установленной точке отсчета Хнач прибавляется ширина интервала h, и находится верхняя граница первого интервала (она же нижняя граница второго интервала). Продолжая прибавлять ширину интервала к предыдущему значению, определяются границы второго, третьего и т.д. интервалов.

В приведенном примере границы первого интервала положим равными 2,5005 и 2,5055 так, чтобы этот участок включал наименьшее значение 2,502. Границы второго интервала определяются следующим образом:

2,5055 + 0,005 = 2,5105.

Аналогично вычисляются границы следующих интервалов. При этом необходимо удостовериться, что последний интервал включает максимальное значение случайной величины Хmax, в противном случае меняя Хнач или изменяя ширину интервала, пересчитывают границы интервалов.

Желательно, чтобы никакие значения наблюдений не попадали на границу интервала, для этого, если значения данных (значения случайной величины), например, имеют 2 знака после запятой, границами интервалов выбирают числа, имеющие 3 знака после запятой. Если все же значение случайной величины оказалось равным границы интервала, то это значение случайной величины следует считать принадлежащим нижнему интервалу.

 Далее вычисляются середины интервалов по формуле:

середина интервала =

Шаг 4

Для определения частот попадания значений контролируемого параметра внутрь каждого из интервалов составляется таблица, в которой указываются: границы интервалов, середины интервалов, частота попадания и т.д. Для подсчета частот, приходящихся на каждый интервал, используются условные значки (наклонные черточки), сгруппированные по пять (Таблица 3).

Таблица 3

Интервал	Середина интервала, хi	Подсчет частот	Частота, fi
2,5005-2,5055 2,5055-2,5105 2,5105-2,5155 2,5155-2,5205 2,5205-2,5255 2,5255-2,5305 2,5305-2,5355 2,5355-2,5405  2,5405-2,54455	2,503 2,508 2,513 2,518 2,523 2,528 2,533 2,538 2,543	/ //// /////  //// /////  /////  //// /////  /////  /////  /////  // /////  /////  /////  //// /////  ///// ///// /////  /	1 4 9 14 22 19 10 5 6
итого		-	90

 После заполнения таблицы производится проверка - если  сумма частот (∑f_i) оказалась не равной общему числу значений (n), это означает, что в подсчет частот вкралась ошибка.

Шаг 5

Последним шагом является построение графика гистограммы. По оси абсцисс необходимо откладывать значения параметров качества, по оси ординат – частоту.

Для каждого интервала необходимо построить прямоугольник  (столбик) с основанием, равным ширине интервала h, высота его должна соответствовать частоте попадания данных в этот интервал f_i.

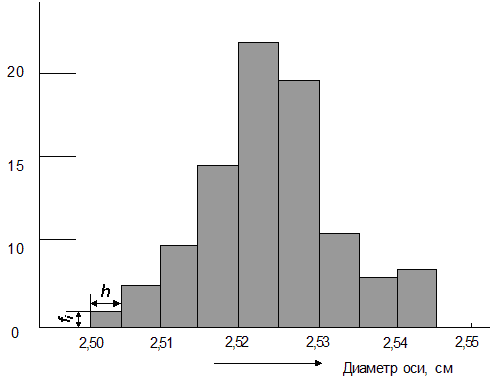
Рис. 1 Гистограмма

На график необходимо нанести линию, представляющую среднее арифметическое, а также линии, представляющие границы допуска, если они есть. В рассматриваемом примере верхняя граница допуска ВГД ограничена значением 2,555 см, нижняя граница допуска НГД - 2,495 см.

Для построенной гистограммы необходимо указать также происхождение данных (наименование изделия, контролируемый параметр, объем партии, число данных, среднее арифметическое значение  и среднее квадратическое отклонение S, период, в течение которого собирались данные и т.п.).

Рассмотрим упрощенный способ вычисления  и S , для чего на основе таблицы 3 составим расчетную таблицу 4.

 Таблица 4  - Расчетная таблица

Интервал	Середина интервала, хi	Частота, fi	ui	uifi	ui²fi
2,5005 – 2,5055 2,5055 – 2,5105 2,5105 – 2,5155 2,5155 – 2, 5205 2,5205 – 2,5255 2,5255 – 2,5305 2,5305 – 2,5355 2,5355 – 2,5405 2,5405 – 2,5455	2,503 2,508 2,513 2,518 2,523 2,528 2,533 2,538 2,543	1 4 9 14 22 19 10 5 6	-4 -3 -2 -1 0 1 2 3 4	-4 -12 -18 -14 0 19 20 15 24	16 36 36 14 0 19 40 45 96
итого		90	-	∑uifi = 30	∑ui2fi = 302

 

В таблице значение «ноль» присвоено тому интервалу, которому соответствует максимальная частота (для интервала 2,5205 – 2,5255 частота f = 22, u = 0). От этого значения (u = 0) в сторону уменьшения значений измерений записывают значения u_i, всякий раз на единицу меньше предыдущего –1, -2, -3, …, а в сторону увеличения значений измерения – всякий раз на единицу больше предыдущего 1, 2, 3,…

Взаимосвязь между х и u выражаются следующим уравнением:

u_i = (х_i – х_{u = 0}) / h,

где    х_{u = 0} – середина участка, для которого u = 0; h – ширина интервала.

 Следует записать произведения величин u_i на f_i в столбец u_if_i, а произведения u_i на u_if_i  в столбец u_i²f_i.

 Составление такой таблицы позволяет произвести вычисления статистических характеристик и S по следующим формулам

                                                     = х_{u = 0} + h (∑u_if_i / n)                                        

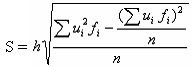
Для данного примера вычислим и S:

 = 2,523 + 0,005 (30/90) = 2,5247см,

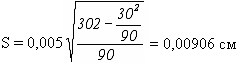
 Можно вычислить  и S и без составления расчетной таблицы, но эти расчеты будут более трудоемкими:

 = Σх_i /n,

Изобразим гистограмму в окончательном виде

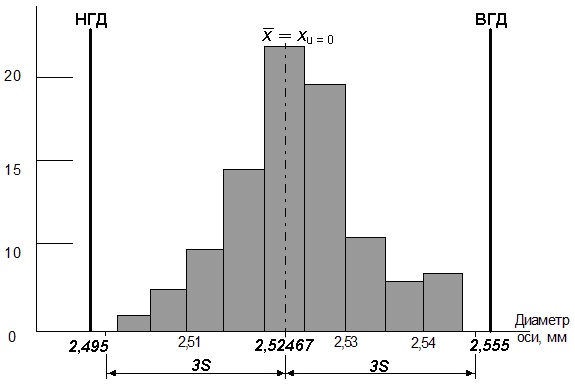
Рис. 2 Гистограмма

Таблица 5 - Данные указываемые при построении гистограммы

Наименование изделия
Тип контроля
Контролируемый параметр
Объем партии
Число данных
Период сбора данных
Ф.И.О. контролера
Ф.И.О. составителя гистограммы

Если на гистограмме от руки провести кривую распределения данных по частоте, представляющую собой среднее арифметическое,  то можно определить вид распределения гистограммы и соотношение значений контрольных нормативов.

Построенная на рис. 2 гистограмма отображает нормальное распределение случайной величины. Среднее значение гистограммы приходится практически на середину нормируемого размаха данных (середину поля допуска 2,525). Наивысшая частота оказывается в середине и постепенно снижается к обоим концам.

Гистограмма удовлетворяет полю допуска. Вероятность появления брака р составляет 0,27 %. Необходимо усилить контроль процесса, провести анализ факторов, влияющих на разброс, и провести мероприятия по улучшению состояния процесса.

 Полученная в результате анализа гистограммы информация может быть легко использована для построения и исследования причинно-следственной диаграммы, что повысит обоснованность мер, намеченных для улучшения процесса.