Лабораторна робота 8 згинання статично невизначуваної двохопорної балки

Мета робота : експериментально визначити прогин та кут повороту перерізів балки і порівняти їх з теоретичними значеннями.

Обладнання: двохопорна статично невизначувана балка, індикатори годинникового типу.

Загальні відомості

Балка називається статично невизначуваною, якщо кількість невідомих реакцій перевищує кількість можливих незалежних рівнянь рівноваги. Різниця між ними є ступенем статичної невизначуваності балки.

Розрахунок статично невизначуваних балок відбувається за методом сил чи методом переміщень. За методом сил розрахунок статично невизначуваної балки має наступну послідовність.

1. Визначається ступінь статичної невизначуваності балки за формулою:

, (8.1)

де К- кількість замкнених контурів балки; Ш - число простих шарнірів.

2. Будується основна система у вигляді геометрично незмінної статично визначуваної балки, шляхом відкидання “зайвих” в’язів.

3. В напрямку відкинутих “зайвих” в’язів прикладаються їхні невідомі реакції 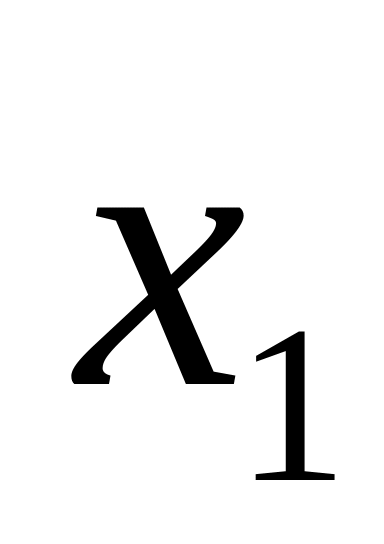, , 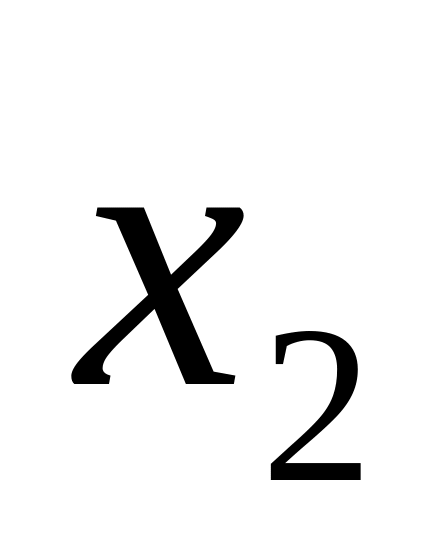... , 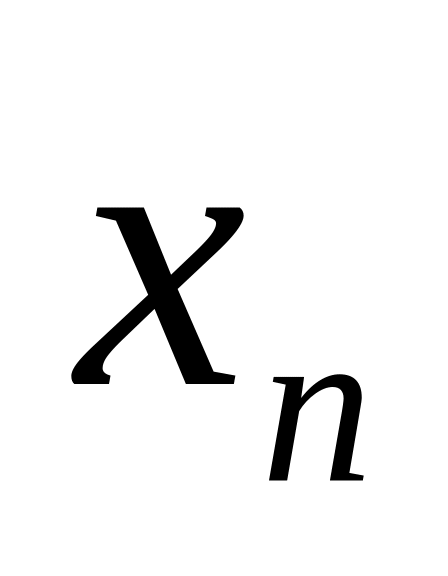та зовнішні навантаження. Таким чином будується еквівалентна система.

4. Складаються канонічні рівняння методу сил, що відображають умови еквівалентності основної системи та заданої балки – рівність нулю переміщень в напрямку відкинутих в’язів.

5. Визначаються коефіцієнти та вільні члени канонічних рівнянь.

6. Розв’язується система рівнянь, визначаються реакції у відкинутих в’язях.

7. Будуються дійсні епюри поперечних сил і згинаючих моментів балки.

8. Виконується кінематична перервірка правильності розрахунку балки.

Експериментальна частина лабораторної роботи виконується на установці, що показана на рис. 8.1. Балка АВ прямокутного поперечного перерізу розмірами dхh та довжиною l жорстко защемлена кінцем В і має шарнірно-рухому опору А.

Експериментальна частина роботи подібна до лабораторної роботи №7.

Розглянемо визначення розрахункових значень прогину перерізу D і кута повороту перерізу А. Застосуємо метод сил згідно до приведеної вище схеми.

Обчислимо ступінь статичної невизначуваності балки

.

Основну систему отримаємо відкиданням “зайвої” в’язі А. Прикладемо до основної системи зовнішню силу Р і реакцію відкинутої в’язі , та отримаємо еквівалентну систему.

Канонічне рівняння методу сил для один раз статично невизначуваної балки має вигляд:

. (8.2)

Для визначення коефіцієнтів , цього рівняння будуємо вантажну М_р й одиничну епюри згинаючих моментів.

За методом Мора по правилу Верещагіна визначаємо коефіцієнти канонічного рівняння (8.2):

, (8.3)

, (8.4)

де - площа одиничної епюри ; - ордината в точці центру її площі; Ω_P – площа вантажної епюри М_P; - ордината епюри під центром площі епюри М_P.

Підставляємо коефіцієнти , в канонічне рівняння та розв’язуємо його. Знаходимо реакцію відкинутого зв’язку А - :

.

Статична невизначуваність балки розкрита. Будуємо дійсну епюру згинаючих моментів . Виконуємо кінематичну перевірку епюри . Вона полягає в рівності нулю переміщення в напрямку відкинутого зв’язку - :

, (8.5)

де - площа епюри ; - значення на епюрі на рівні центру площі епюри .

До основної системи в перерізі D прикладаємо одиничну силу P=1, будуємо епюру згинаючих моментів від дії цієї сили. Перемножуємо за методом Мора епюри та знаходимо розрахункове значення прогину перерізу D балки:

, (8.6)

де - значення на епюрі на рівні центру площі епюри .

Прикладаємо до основної системи одиничний момент у перерізі А, будуємо епюру згинаючих моментів від його дії і, перемножуючи епюри та за методом Мора, обчислюємо розрахункове значення кута повороту перерізу А:

,

де - значення на епюрі на рівні центру площі епюри .