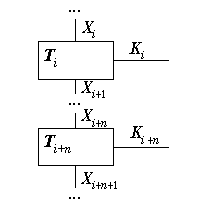6. Содержание отчета

После того как Вы добьётесь приемлемого результата, необходимо показать преподавателю итоговую работу в виде полученных вариантов паролей и составить отчет.

Отчёт должен содержать титульный лист, описание выполненных работ, в котором должны быть представлены краткие теоретические выкладки, возникшие трудности при выполнении работы и пути их решения, а также полученные Вами пароли для каждой из программ, с указанием шаблона пароля, а также результата проверки его стойкости.

Лабораторная работа № 9. Криптографические системы шифрования и их применение в электронном документообороте

1. Цели и задачи работы

В данной лабораторной работе необходимо изучить мировые тенденции развития систем защиты электронного документооборота и хранении данных в архивах.

2. Основные теоретические сведения

На пороге тысячелетий информация становится одним из наиболее важных и ценных продуктов, созданных человеком. Именно поэтому большое значение придается ее защите от неправомерного получения и использования.

Еще 15-20 лет назад, говоря о защите информации, понимали исключительно задачу сохранения секретной информации от не допущенных к ней лиц. Бурное развитие информационных технологий привело не только к революции в сфере обращения информации (создания, хранения, передачи информации), но и к пересмотру содержания самого понятия защиты информации. Сейчас принято выделять три главные составляющие этого понятия, а именно: конфиденциальность, целостность и доступность информации.

Под обеспечением конфиденциальности информации понимается решение проблемы защиты информации от ознакомления с ее содержанием лиц, не имеющих права доступа к ней. Обеспечение целостности – гарантирование невозможности несанкционированного изменения информации. И, наконец, доступность – категория, характеризующая возможность потребления (использования) информации законными пользователями. В некоторых случаях приходится говорить еще о необходимости обеспечения неотказуемости от переданной информации и необходимости разработки методов идентификации сторон в процессе информационного взаимодействия.

Частично ряд из отмеченных задач по защите информации решается на основе принятия соответствующих нормативно-правовых актов, использования организационных и режимных мер. Вместе с тем большую, если не центральную роль в защите информации играет ранее сверх засекреченная область деятельности – криптография.

Криптография в переводе с греческого означает тайнопись как систему изменения правил написания текстов с целью сделать эти тексты непонятными для непосвященных лиц (не путать с тайнописью, основанной на сокрытии самого факта написания текста, например, симпатическими чернилами и т.п.). Естественно, что используемый способ изменения написания текстов или какая-то часть его, обычно называемая ключом, должны быть неизвестны посторонним лицам.

Зарождение криптографии как способа действий для сохранения в тайне содержания писем, посланий, депеш, секретных приказов и т.п. относят к очень далеким временам, фактически к временам возникновения письменности.

В исторических документах древних цивилизаций Индии, Египта, Месопотамии имеются сведения о системах и способах составления шифрованных писем. Более достоверные сведения о применяемых системах шифров относятся к периодам существования государств древней Греции и древнего Рима. Шифровались религиозные тексты, прорицания жрецов, медицинские рецепты, использовалась криптография и в государственной сфере.

В той или иной степени имели дело с шифрованием текстов или затрагивали эти вопросы в своих трактатах такие исторические фигуры как Полибий, Юлий Цезарь, Платон, Пифагор, Аристотель и др.

Поскольку обоснование надежности шифров в основе своей базируется на математике, естественно, что достаточно сильно криптография была развита в арабских государствах в период их расцвета, в которых в это время жили и работали серьезные ученые-математики. А в 1412 году была даже издана 14-томная энциклопедия научных сведений – «Шауба-аль-Аша» (составитель Шехаб аль Кашканди), в которой содержится целый раздел о криптографии с описанием всех известных на то время способов шифрования текстов.

Эти примеры можно было бы продолжить. Важно отметить, что в течение длительного времени криптография была уделом отдельных талантливых изобретателей, как тех, кто создавал шифры, так и тех, кто пытался их разгадывать. Но постепенно, особенно начиная с XVII-XVIII веков, благодаря исследованиям и работам ряда ученых и, в частности, таких известных как Л. Эйлер, Ф. Эпинус, Д. Кардано, Ф. Виет и др., позднее – К. Шеннон, А. Тьюринг, криптография прочно становится на научную основу.

В настоящее время криптография является самостоятельным, активно развивающимся направлением научных исследований, ее результаты имеют весьма широкую область практических приложений, некоторые из которых ниже будут отмечены.

С гордостью можно отметить, что большой вклад в развитие криптографии как науки внесли наши отечественные ученые, о чем впервые открыто было заявлено в 2002 году на конференции «Московский университет и развитие криптографии в России» (ранее ввиду большой секретности исследований в области криптографии эти сведения были засекречены). К плеяде этих ученых относятся, в частности, такие всемирно известные по своим трудам в других областях научных исследований отечественные ученые как академики А.Н. Колмогоров, В.А. Котельников, А.А. Марков, А.О. Гельфонд, Ю.В. Линник и др.

Россия, кстати, единственная страна, в которой образована и пользуется реальной государственной поддержкой Академия криптографии РФ, имеющая весьма высокий научный потенциал. В ее составе 3 академика и 2 член-корреспондента РАН, более пятидесяти докторов наук. Академия ежегодно проводит большой объем исследований по фундаментальным проблемам криптографии, регулярно выпускает сборники научных трудов в этой области.

В результате деятельности российских ученых, работы ряда крупных научно-исследовательских институтов (один из которых, в частности, описан в произведениях Солженицына А.И.) в Советской России практически с нуля была создана целая отрасль разработки и производства надежных средств криптографической защиты информации (СКЗИ). Она сыграла огромную роль в победе нашей страны в Великой отечественной войне и в ее послевоенном восстановлении в условиях жесткого противостояния с Западом и, к счастью, выжила и в трудных условиях смены в России форм собственности и соответствующего изменения структуры государственной власти.

Среди государственных ведомств наиболее развитых стран, т.е. стран, оказывавших основное влияние на расстановку сил в мире, два ведомства – дипломатическое и военное – просто не могли эффективно выполнять свои функции без надежно функционирующих криптографических. История дипломатии и военных ведомств изобилует примерами напряженного противоборства криптографических служб, противостоящих друг другу в тех или иных конфликтах стран.

Вот некоторые из них.

Разгром в 1914 году двух не самых плохих русских армий – Ранненкампа и Самсонова в Восточной Пруссии – произошел из-за плохой организации шифрованной связи, в результате чего обмен информацией между ними велся в открытую со всеми вытекающими из этого последствиями.

В период советско-финской кампании осуществлялось сотрудничество Швеции, имевшей сильную дешифровальную службу, и Финляндии в области радиоразведки. Швеция передавала своему соседу результаты радиоперехвата и чтения шифрпереписки сухопутных частей Красной Армии и советских ВВС. Это, безусловно, сыграло свою роль в успешной организации упорного сопротивления Финляндии советским войскам.

История с немецкой шифровальной машиной «Энигма», использовавшейся в период второй мировой войны, стала уже одной из легенд криптографии. Дело в том, что эта машина, по оценкам специалистов даже с позиций современного взгляда на эти вопросы, была очень стойкой по отношению к попыткам вскрытия переданной по ней информации, и немецкое командование не опасалось использовать ее для шифрования, в том числе и весьма важной информации. Однако союзническими войсками были разработаны сценарии захвата ключей на кораблях и подводных лодках германского флота, и ряд подобных операций был успешно проведен. К несчастью для Германии, эти факты были оставлены без должного внимания со стороны немецкого командования, должных мер не было принято. В результате английские спецслужбы читали переписку по «Энигме», причем ценность ее была столь велика, что У. Черчилль, которому из этого источника стали известны планы германской бомбардировки Ковентри, предпочел пожертвовать городом, лишь бы не раскрыть и не потерять такой источник информации.

Но, конечно, не только такого рода события определяли судьбу и место криптографии в общественно-экономической и политической жизни стран. В значительно большей степени развитие криптографии определялось содержанием и темпами развития собственно информатики. Каждый раз с появлением новых видов носителей информации, новых способов передачи ее по каналам связи, увеличением скорости передачи и т.п. разрабатывались и соответствующие криптографические средства защиты информации. В настоящее время в мире разработано и поставляется на рынок очень большое разнообразие программных, аппаратных и программно-аппаратных СКЗИ, предназначенных для различных условий применения. Неискушенному потребителю бывает весьма сложно разобраться в этом море продуктов, чтобы выбрать для себя наиболее подходящий из них с точки зрения оптимального соотношения стоимости и эффективности реализации соответствующих защитных свойств, но этот вопрос уже выходит за рамки целей настоящей публикации.

Все приведенные выше исторические примеры относятся к так называемой проблеме обеспечения конфиденциальности информации, причем криптография – единственный из известных способов, позволяющий на строго научном, доказательном уровне решать эту проблему.

Вместе с тем сохранение информации в тайне (когда это необходимо) – не единственная проблема, возникающая в процессе производства, хранения и обмена информацией. Важными составляющими являются обеспечение целостности и подлинности информации. Оказывается, что криптография и здесь дает надежные средства решения этой задачи. Это хорошо иллюстрирует ситуация с электронным документооборотом, электронной торговлей, электронной коммерцией и т.п. В каждой из этих сфер деятельности важнейшая задача – гарантированное подтверждение целости и подлинности пересылаемых (получаемых) по электронным средствам документов, денежных переводов, счетов и т.д. Эта задача успешно решается средствами так называемой электронной цифровой подписи (ЭЦП), в основе которых лежат криптографические преобразования.

Здесь, как и в предыдущем случае, к настоящему времени разработано уже несколько вариантов средств, реализующих различные форматы ЭЦП. Но в отличие от предыдущего случая такое разнообразие во многом мешает эффективному использованию технологий ЭЦП в указанных выше областях, поскольку существенно затрудняет взаимодействие между собой различных структур, оснащенных разными средствами ЭЦП. Безусловно, это трудности временные, нисколько не бросающие тень собственно на криптографию. Более того, уже разработаны способы решения этой проблемы за счет соответствующего построения системы так называемых удостоверяющих центров и введения режимов взаимного признания подписей (технология так называемой кросс-сертификации, которая с выходом на арену Федерального агентства по информационным технологиям как структуры, выполняющей функции УФО (см. закон об ЭЦП), приобретает уже реальную возможность внедрения в практику уже в масштабах и интересах страны в целом). Но эта тема, по-видимому, заслуживает особого рассмотрения.

И наконец, еще одна составляющая понятия защиты информации, которая реально может встретиться в практике электронного документооборота, электронной торговли и т.п., - проблема неотказуемости от переданного документа (послания и т.п.). Оказывается, эта проблема опять же решается все теми же средствами ЭЦП (читай: криптографическими методами), причем не менее надежно, чем в случае обычной подписи на основе использования, при необходимости, графологических экспертиз.

Помимо упомянутых выше, а также ставших уже достаточно общеизвестными приложениями криптографии в области защищенного обмена информацией по сетям связи общего пользования, в частности, по интернету, защиты электронных баз данных, закрытия информации, хранящейся на жестких дисках, на «интеллектуальных» картах и т.п., имеются и менее известные примеры применения криптографических методов, также заслуживающие упоминания.

Так, известно широкое распространение голограмм для защиты от подделок документов, различного рода продукции и т.д. Оказывается, что наиболее надежная голографическая защита может быть построена на основе помещения в голограмму абсолютно надежно защищенного методами криптографии цифрового кода, содержащего всю необходимую идентификационную информацию о защищаемом объекте. Такие технологии уже разработаны российскими учеными, правда, пока их практическая реализация выглядит достаточно сложной.

Другой пример – проблема защиты контрольно-кассовых машин (ККМ) от изменения недобросовестными пользователями содержащейся в их фискальной памяти информации о результатах торгового дня. К настоящему времени уже разработаны (кстати, нашими отечественными фирмами) криптографические способы защиты от такого рода злоупотреблений, позволяющие практически со стопроцентной надежностью проверять контрольным органам подобное вмешательство в фискальную память ККМ. Более того, при оснащении контролируемых объектов соответствующими средствами связи можно было бы такой контроль делать дистанционно и незаметно для объекта контроля. Последнее удовольствие, правда, пока весьма дорогое.

Говоря о современном состоянии криптографии, следует сказать, что она переживает этап бурного развития. Этому способствуют два обстоятельства. Во-первых, стремительно развиваются ИТ-технологии, являющиеся основной сферой приложений для криптографии. Во-вторых, криптография, наконец, вышла в открытый мир, и в ней нашли поле приложения своих сил большое количество молодых, энергичных и талантливых ученых.

К числу наиболее интересных и значительных достижений современности в криптографии, безусловно, следует отнести изобретение американскими учеными Диффи и Хеллманом в 70-десятых годах прошлого столетия нового принципа построения шифров, не требующего организации довольно трудоемкого процесса постоянного защищенного снабжения связывающихся сторон секретными ключами. В новом способе эти ключи вырабатываются с помощью специальной процедуры обмена некоторыми данными по обычным открытым каналам связи. К сожалению, идея этого способа основана на глубоких математических результатах и не может быть доступно изложена в популярной форме. Вместе с тем, хотя этот способ уже широко используется на практике, некоторые основополагающие математические гипотезы, на которых он основан, пока строго не доказаны. Это создает определенную тревогу с точки зрения надежности такого рода шифровальных систем.

Еще одним направлением исследований, сулящим большие перспективы для криптографии, являются работы в области так называемой «квантовой криптографии», основанной уже на результатах теоретической физики. И хотя на пути практической реализации этого направления встретились серьезные трудности научно-технического характера, специалисты достаточно обоснованно надеются на возможность их преодоления, и тогда мы станем свидетелями новых крупных успехов в теоретической и практической криптографии.

В заключение один конкретный пример использования криптографии в банковской сфере. Речь идет об автоматизированных платежных системах с дистанционным управлением банковским счетом на базе общедоступных (открытых) сетей связи (пластиковые карты плюс интернет, системы мобильной связи и т.п.). Здесь такие важные функции платежных систем, как защита передаваемых по каналам общей связи платежных поручений, юридическая значимость электронных транзакций, неотказуемость участников системы от совершенных операций должны базироваться исключительно на криптографических средствах защиты.

Таким образом, криптографические методы, характеризующиеся большими возможностями по обеспечению конфиденциальности и достоверности информации, а также по обеспечению «неотказуемости» от авторства в процессе обмена информацией, находят себе применение во все более и более многочисленных приложениях. Можно предположить в связи с этим, что определенное знакомство с криптографией, ее методами и возможностями в недалеком будущем потребуется каждому пользователю электронных средств обработки и обмена информацией. Более того, оптимисты от криптографии считают, что криптография рано или поздно станет «третьей грамотностью» наряду со «второй» грамотностью – владением компьютером и информационными технологиями.

Человек - существо социальное, вот уже много тысячелетий он живет в обществе себе подобных. И вполне естественно, что одной из важнейших его способностей является умение общаться с другими людьми - передавать им сведения о том, что происходит в окружающем их мире, и о фактах своей субъективной реальности. Вторая сигнальная система - речь - по праву считается одним из важнейших отличительных признаков, качественно выделяющих человечество из животного мира. Характер информационного обмена между членами даже самого дикого племени многократно превышает по своей сложности все то, что можно увидеть у животных. Коммуникация в человеческом обществе имеет еще один отличительный признак - она узко избирательна. Мы разговариваем с разными людьми совершенно по-разному, и то, что сообщаем одним, стараемся скрыть от других.

Таким образом, с зарождением человеческой цивилизации возникло умение сообщать информацию одним людям так, чтобы она не становилась известной другим. Пока люди использовали для передачи сообщений исключительно голос и жесты, сделать это обычно не составляло особого труда - нужно было лишь исключить присутствие в непосредственной близости от разговаривающих тех людей, для которых сообщаемые сведения не предназначены. Однако иногда внешние факторы накладывали на поведение собеседников ограничения, не позволявшие им укрыться от посторонних ушей и глаз для проведения конфиденциальной беседы. Для действия в подобных обстоятельствах была создана, а точнее сложилась сама собой, система кодированных речью или жестами сообщений. В различных ситуациях она носила совершенно различный характер - от отдельного тайного знака, говорящего о наступлении определенного события, до развитых секретных языков, позволявших выражать мысли практически любой сложности. Даже в самом простейшем случае это была по своей сути вторая сигнальная система в миниатюре, предназначенная для передачи ограниченного набора сведений и известная как правило лишь небольшой группе посвященных, осколок - большой или маленький - альтернативного языка, и именно она положила начало развившемуся позже искусству тайно передавать сообщения.

Конечно, использование развитого "секретного" языка для защиты передаваемых данных обеспечивает гораздо большую свободу в коммуникации, чем несколько тайных знаков, о которых участники договорились накануне, однако этот путь имеет и гораздо большие издержки. За всеми посвященными уследить трудно, и рано или поздно такой язык станет понятным тем, от кого пытаются скрыть разговор. В этом случае возникнет необходимость его заменить другим, разработать же достаточно мощный язык и обучить ему нужное количество людей весьма затруднительно и накладно, а сделать это оперативно - невозможно. Поэтому подобный подход к проблеме проходит только в особых случаях, когда тому благоприятствуют обстоятельства. Так, он использовался американцами во время второй мировой войны: корабли ВМФ США осуществляли связь на языке малочисленного и компактно проживающего индейского племени. На каждом корабле было несколько индейцев-"шифровальщиков", у противника не было практически никаких шансов раздобыть себе такого "криптографа".

Надо заметить, что тема передачи сообщения посредством тайных знаков активно эксплуатировалась писателями и сценаристами приключенческого жанра. Вспомните фильм "Вариант омега", в котором советский разведчик передавал сигнал о том, что он работает под контролем немецкой контрразведки, ставя или пропуская точку после определенной фразы сообщения. Но немцы этот фокус раскусили и каждый раз аккуратно вырезали кусок магнитной ленты с точкой. Это, однако, им не помогло - доблестный советский разведчик передал свой сигнал выбором цветов во время покупки их у цветочника-связника. Кстати, о цветах - вспомните горшочек с цветком на подоконнике проваленной явочной квартиры, который так легкомысленно проигнорировал... Язык тайной передачи сообщений жестами активно используется и в наши дни представителями некоторых криминальных "специальностей", например, шулеров - во время "работы" пара шулеров ведет весьма оживленную беседу, незаметную ненаметанному глазу непрофессионала.

С возникновением письменности задача обеспечения секретности и подлинности передаваемых сообщений стала особенно актуальной. Действительно, сообщение, переданное словесно или показанное жестами, доступно для постороннего только в тот краткий промежуток времени, пока оно "в пути", а в его авторстве и подлинности у получателя никаких сомнений быть не может, потому что он видит своего собеседника. Иное дело, когда сообщение записано - оно уже живет отдельной жизнью и имеет свой путь, зачастую далеко расходящийся с путем человека, его создавшего. Записанное на бумаге сообщение существует в материальном мире гораздо более длительный промежуток времени, и у людей, желающих ознакомиться с его содержанием против воли отправителя и получателя, появляется гораздо больше шансов сделать это. Поэтому именно после возникновения письменности появилось искусство тайнописи, искусство "тайно писать" - набор методов, предназначенных для секретной передачи записанных сообщений от одного человека другому.

Данные о первых способах тайнописи весьма обрывочны. Предполагается, что она была известна в древнем Египте и Вавилоне. До нашего времени дошли указания на то, что искусство секретного письма использовалось в древней Греции. Первые действительно достоверные сведения с описанием метода шифрования относятся к периоду смены старой и новой эры и описывают шифр Цезаря - способ, которым Юлий Цезарь прятал свои записи от излишне любопытных глаз. С высоты достижений современной криптографии шифр Цезаря предельно примитивен: в нем каждая буква сообщения заменялась на следующую за ней по алфавиту. Однако для того времени, когда умение читать и писать было редким исключением, его криптостойкости вполне хватало. Использование шифра решало проблему секретности передаваемого сообщения, а проблема его подлинности решалась практически сама собой:

во-первых, для человека, не знавшего шифр, было невозможно внести осмысленные изменения в зашифрованные сообщения, носившие исключительно текстовый характер, а изменения, внесенные наобум приводили к тому, что после расшифрования получался бессмысленный набор букв;

во-вторых, практически до совсем еще недавних по историческим меркам времен отправляемые сообщения записывались от руки, а каждый человек имеет свой индивидуальный, присущий только ему почерк, который очень трудно воспроизвести другому человеку; запомнить почерк даже нескольких десятков наиболее важных своих корреспондентов, - а больше ни у кого и не было, - не составляет особого труда.

Человечество изобрело большое число способов секретного письма, многие из них были известны еще в древности. В некоторых способах тайного письма используются физические особенности носителей информации. Так симпатические чернила исчезают вскоре после написания ими текста или невидимы с самого начала. Но их можно снова сделать видимыми, обработав документ специальным химическим реактивом или осветив лучами определенной части спектра, обычно - ультрафиолетом. Стеганография предполагает, что передаваемый текст "растворяется" в сообщении большего размера с совершенно "посторонним" смыслом. Но если взять и извлечь из него некоторые символы по определенному закону, например - каждый второй, или третий, и т.д., получим вполне конкретное тайное сообщение. Шифрование является преобразованием сообщения по определенным правилам, что делает его бессмысленным набором знаков для непосвященного в тайну шифра человека.

Классифицировать способы засекречивания передаваемых сообщений можно по-разному, однако определяющих факторов всего два:

используются ли для засекречивания свойства материальных носителей и материальной среды передачи информации или оно осуществляется независимо от них;

прячется ли секретное сообщение или оно просто делается недоступным для всех, кроме получателя.

Как отмечено выше, большое число способов засекретить сообщение связано с воздействием на его носитель как на материальный объект. Это очень интересная тема, однако она является предметом изучения физики и химии, и никакого отношения к теории информации не имеет. Для массового практического применения гораздо больший интерес представляют методы защиты данных, которые опираются исключительно на свойства самих данных и никак не связаны с особенностями их физического представления. Образно говоря, при использовании методов данного типа барьер между собственно сообщением и злоумышленником, желающим его прочитать или исказить, возводится исключительно из самой информации. Речь в дальнейшем пойдет только о таких способах защиты.

В зависимости от ответа на второй из приведенных выше вопросов получаются различные классы способов засекречивания данных - стеганография и шифрование. Если рассматривать информацию отдельно от ее материального представления, то где же ее тогда можно спрятать? Ответ однозначен: только в еще большем массиве информации - как иголку в стоге сена. В этом и заключается принцип действия стеганографии. Например, мы отправляем нашему корреспонденту по электронной почте файл с растровой черно-белой картинкой, в котором наименее значащий бит в коде яркости каждой точки изображения будет элементом нашего тайного сообщения. Получатель письма извлечет все такие биты и составит из них "истинное" сообщение. Картинка, присутствующая здесь только для отвода глаз, так и останется для непосвященных простой картинкой. Стеганография бывает полезна, когда необходимо не просто передать секретное сообщение, а секретно передать секретное сообщение, то есть скрыть сам факт передачи секретного сообщения. Такой способ ведения тайной коммуникации, однако, имеет ряд недостатков:

во-первых, трудно обосновать его стойкость - вдруг злоумышленникам станет известен способ "подмешивания" секретных данных к "болванке" - массиву открытых данных;

во-вторых, при его использовании объем передаваемых или хранимых данных резко увеличивается, что отрицательно сказывается на производительности систем их обработки;

Другой подход - не скрывать факт передачи сообщения, но сделать его недоступным посторонним. Для этого сообщение должно быть записано так, чтобы с его содержимым не мог ознакомиться никто за исключением самих корреспондентов - в этом и заключается суть шифрования. И криптография возникла именно как практическая дисциплина, изучающая и разрабатывающая способы шифрования сообщений.

Вернемся к истории. Чем оживленнее велась переписка в обществе, тем большая ощущалась потребность в средствах ее засекречивания. Соответственно, возникали все более совершенные и хитроумные шифры. Сначала при заинтересованных лицах появились шифровальщики, потом группы из нескольких шифровальщиков, а затем и целые шифровальные отделы. Когда объемы подлежащей закрытию информации стали критическими, в помощь людям были созданы механические устройства для шифрования. Надо сказать, что основными потребителями криптографических услуг были дипломатические и шпионские миссии, тайные канцелярии правителей и штабы войсковых соединений. Для этого этапа развития криптографии характерно следующее:

защите подвергались исключительно текстовые сообщения, написанные на естественных языках - других типов дискретно представленных данных просто не существовало;

шифрование сначала осуществлялось вручную, позднее были изобретены сравнительно несложные механические приспособления, поэтому использовавшиеся тогда шифры были достаточно простыми и несложными;

криптография и криптоанализ были скорее искусством, чем наукой, научный подход к построению шифров и их раскрытию отсутствовал;

криптография использовалась в очень узких сферах - только для обслуживания высших правящих слоев и военной верхушки государств;

основной задачей криптографии была защита передаваемых сообщений от несанкционированного ознакомления с ними, поскольку шифровались исключительно текстовые сообщения, никаких дополнительных методов защиты от навязывания ложных данных не применялось - вероятность получить нечто осмысленное после расшифрования искаженного зашифрованного текста была ничтожно мала в силу огромной избыточности, характерной для естественных языков.

Появление в середине нашего столетия первых электронно-вычислительных машин кардинально изменило ситуацию. С проникновением компьютеров в различные сферы жизни возникла принципиально новая отрасль хозяйства - информационная индустрия. Объем циркулирующей в обществе информации с тех пор стабильно возрастает по экспоненциальному закону - он примерно удваивается каждые пять лет. Фактически, на пороге нового тысячелетия человечество создало информационную цивилизацию, в которой от успешной работы средств обработки информации зависит само благополучие и даже выживание человечества в его нынешнем качестве. Произошедшие за этот период изменения можно охарактеризовать следующим образом:

объемы обрабатываемой информации возросли за полвека на несколько порядков;

сложилось такое положение вещей, что доступ к определенным данным позволяет контролировать значительные материальные и финансовые ценности; информация приобрела стоимость, которую во многих случаях даже можно подсчитать;

характер обрабатываемых данных стал чрезвычайно многообразным и более не сводится к исключительно текстовым данным;

информация полностью "обезличилась", т.е. особенности ее материального представления потеряли свое значение - сравните письмо прошлого века и современное послание по электронной почте;

характер информационных взаимодействий чрезвычайно усложнился, и наряду с классической задачей защиты передаваемых текстовых сообщений от несанкционированного прочтения и искажения возникли новые задачи сферы защиты информации, ранее стоявшие и решавшиеся в рамках используемых "бумажных" технологий - например, подпись под электронным документом и вручение электронного документа "под расписку" - речь о подобных "новых" задачах криптографии еще впереди;

субъектами информационных процессов теперь являются не только люди, но и созданные ими автоматические системы, действующие по заложенной в них программе;

вычислительные "способности" современных компьютеров подняли на совершенно новый уровень как возможности по реализации шифров, ранее немыслимых из-за своей высокой сложности, так и возможности аналитиков по их взлому.

Перечисленные выше изменения привели к тому, что очень быстро после распространения компьютеров в деловой сфере практическая криптография сделала в своем развитии огромный скачок, причем сразу по нескольким направлениям:

во-первых, были разработаны стойкие блочные шифры с секретным ключом, предназначенные для решения классической задачи - обеспечения секретности и целостности передаваемых или хранимых данных, они до сих пор остаются "рабочей лошадкой" криптографии, наиболее часто используемыми средствами криптографической защиты;

во-вторых, были созданы методы решения новых, нетрадиционных задач сферы защиты информации, наиболее известными из которых являются задача подписи цифрового документа и открытого распределения ключей.

Как видим, термин "криптография" далеко ушел от своего первоначального значения - "тайнопись", "тайное письмо". Сегодня эта дисциплина объединяет методы защиты информационных взаимодействий совершенно различного характера, опирающиеся на преобразование данных по секретным алгоритмам, включая алгоритмы, использующие секретные параметры. Термин "информационное взаимодействие" или "процесс информационного взаимодействия" здесь обозначает такой процесс взаимодействия двух и более субъектов, основным содержанием которого является передача и/или обработка информации. По большому счету, криптографической может считаться любая функция преобразования данных, секретная сама по себе или зависящая от секретного параметра S:

T' = f(T), или T' = f(T,S).

Теперь перейдем к характеристикам задач, решаемых криптографическими методами в наши дни. Информационные взаимодействия между различными субъектами могут носить различный, порой весьма запутанный характер, соответственно существуют различные угрозы их нормальному осуществлению. Для того, чтобы поставить задачу защиты информации, необходимо подробно ответить на вопросы трех следующих групп:

1. Что именно мы намереваемся защищать?

Эта группа вопросов относится к информационному процессу, нормальное течение которого мы намерены обеспечить:

кто является участником информационного процесса;

каковы задачи участников информационного процесса;

каким именно образом участники процесса выполняют стоящие перед ними задачи;

2. От чего мы собираемся защищать нашу систему?

Эта группа вопросов охватывает возможные отклонения от нормального течения процесса информационного взаимодействия:

каков критерий "нормального" прохождения процесса информационного взаимодействия;

какие возможны отклонения от "нормы";

3. От кого мы собираемся защищать нашу систему?

Эта группа вопросов относится к тем субъектам, которые предпринимают те или иные действия для того, чтобы отклонить процесс от нормы:

кто может выступать в качестве злоумышленника, то есть предпринимать усилия для отклонения процесса информационного взаимодействия от нормального течения;

каких целей добиваются злоумышленники;

какими ресурсами могут воспользоваться злоумышленники для достижения своих целей;

какие действия могут предпринять злоумышленники для достижения своих целей.

Развернутый ответ на первый вопрос является моделью информационного процесса. Подробный ответ на второй вопрос должен включать критерий "нормальности" процесса и список возможных отклонений от этой "нормальности", называемых в криптографии угрозами, - ситуаций, которые мы бы хотели сделать невозможными. Субъект, препятствующий нормальному протеканию процесса информационного взаимодействия, в криптографической традиции называется "злоумышленником", в качестве него может выступать в том числе и законный участник информационного обмена, желающий добиться преимуществ для себя. Развернутый ответ на третий вопрос называется в криптографии моделью злоумышленника. Злоумышленник - это не конкретное лицо, а некая персонифицированная сумма целей и возможностей, для которой справедлив принцип Паули из физики элементарных частиц: два субъекта, имеющие идентичные цели и возможности по их достижению, в криптографии рассматриваются как один и тот же злоумышленник.

Ответив на все перечисленные выше вопросы, вы получите постановку задачи защиты своего информационного процесса. Вот пример - задача защиты программного обеспечения (п/о) от незаконного копирования:

1. Субъекты этого процесса - поставщик п/о и пользователь, в рамках процесса они выполняют следующие действия:

поставщик передает пользователю дистрибутивный носитель п/о;

пользователь инсталлирует п/о на своем компьютере, получая при этом рабочую копию п/о;

пользователь использует рабочую копию п/о, запуская на выполнение программы, входящие в ее состав;

пользователь может уничтожить рабочую копию п/о на одном компьютере и инсталлировать ее на другом.

2. Нормальным течением информационного процесса является ситуация, при которой рабочая копия п/о установлена и используется только на одном компьютере. Отклонением является инсталляция и использование рабочих копий п/о более чем на одном компьютере.

3. Использовать более одной копии программного обеспечения могут попытаться сделать следующие субъекты:

законный владелец п/о, располагающий дистрибутивным комплектом, может установить еще одну рабочую копию п/о, при этом он может использовать как уже инсталлированную рабочую копию п/о, так и дистрибутивный комплект;

человек, имеющий доступ к компьютеру с инсталлированным п/о, может попытаться скопировать его на другой компьютер и использовать там.

Очевидно, что оба злоумышленника имеют разные возможности по достижению своих целей, и задача защиты в первом случае (злоумышленник - владелец п/о) намного тяжелее, чем во втором (у злоумышленника нет дистрибутива п/о).

Разные задачи из сферы защиты информации отличаются друг от друга именно различными ответами на приведенные выше вопросы. Только после детального и исчерпывающего ответа на все вопросы задача защиты информационного процесса может считаться поставленной и вы можете приступить к проектированию защиты.

Подведем итоги:

криптография - это набор методов защиты информационных взаимодействий от отклонений от их нормального, штатного протекания, вызванных злоумышленными действиями различных субъектов, методов, базирующихся на секретных алгоритмах преобразования информации, включая алгоритмы, не являющиеся собственно секретными, но использующие секретные параметры;

исторически первой задачей криптографии была защита передаваемых текстовых сообщений от несанкционированного ознакомления с их содержанием, что нашло отражение в самом названии этой дисциплины, эта защита базируется на использовании "секретного языка", известного только отправителю и получателю, все методы шифрования являются лишь развитием этой философской идеи;

с усложнением информационных взаимодействий в человеческом обществе возникли и продолжают возникать новые задачи по их защите, некоторые из них были решены в рамках криптографии, что потребовало развития принципиально новых подходов и методов.

На этом вступительный выпуск завершается. Следующий, первый выпуск, будет содержать краткий обзор задач по защите информационных взаимодействий, стоящих перед криптографией в наши дни и решаемых в ее рамках.

криптография - это дисциплина, изучающая способы защиты процессов информационного взаимодействия от целенаправленных попыток отклонить их от условий нормального протекания, основанные на криптографических преобразованиях, то есть преобразованиях данных по секретным алгоритмам. С давних времен вплоть до настоящего время важнейшей задачей криптографии является защита передаваемых по каналам связи или хранящихся в системах обработки информации данных от несанкционированного ознакомления с ними и от преднамеренного их искажения. Криптография решает указанную задачу посредством шифрования защищаемых данных, что предполагает использование двух следующих взаимно обратных преобразований:

- перед отправлением данных по линии связи или перед помещением на хранение они подвергаются зашифрованию; - для восстановления исходных данных из зашифрованных к ним применяется процедура расшифрования.

На следующем ниже рисунке 1 приведена схема преобразования данных при шифровании:

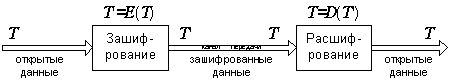
Схема преобразования данных при шифровании.

Шифром называется пара алгоритмов, реализующих каждое из указанных преобразований. Секретность второго из них делает данные недоступными для несанкционированного ознакомления, а секретность первого делает невозможным навязывание ложных данных. Получение открытых данных по зашифрованным без знания алгоритма расшифрования называется дешифрованием. Изначально шифрование использовалось для защиты передаваемых сообщений от обеих указанных угроз, однако позднее было показано, что оно может защитить данные от несанкционированной модификации только если выполнены определенные условия, а именно:

- шифруемое сообщение содержит большую избыточность; - процесс шифрования хорошо "перемешивает" структурные единицы сообщения (биты, символы и т.д.).

Так как эти условия выполняются далеко не всегда, то в общем случае шифрование не является средством имитозащиты - защиты от навязывания ложных данных. Этой проблеме будет посвящено один или несколько будущих выпусков, а пока мы про нее на время "забудем".

Каким же условиям должен удовлетворять шифр? Ну прежде всего, процедура расшифрования должна всегда восстанавливать открытое сообщение в его исходном виде. Иными словами, для каждого допустимого сообщения T преобразования за- и расшифрования должны удовлетворять следующему свойству:

T = D(E(T))

Второе условие, которому должен удовлетворять шифр, следующее: он должен ... шифровать данные, то есть делать их непонятными для непосвященного.

Другими словами, не должно существовать легко прослеживаемых связей между исходными и зашифрованными данными. Кроме того, шифр должен быть криптостойким, то есть устойчивым к попыткам дешифрования сообщений. Понятно, что вопрос стойкости шифров является главным в этой отрасли криптографии, и его рассмотрение мы начнем с выяснения того, что же может служить мерой стойкости.

Отправленное сообщение до поступления к получателю является для него и, естественно, для злоумышленника неопределенным - если это было бы не так, тогда не было бы вообще никакого смысла его посылать. Пусть возможна отправка сообщений T1,T2,...,Tn с вероятностью p1, p2,..., pn соответственно. Тогда мерой неопределенности сообщения для всех, кто обладает этой априорной информацией, может служить величина математического ожидания логарифма вероятности одного сообщения, взятая со знаком "минус"; по некоторым соображениям в качестве основания логарифма удобно выбрать 2:

Эта величина имеет вполне понятный физический смысл: количество битов информации, которое необходимо в среднем передать, чтобы полностью устранить неопределенность. Если никакой априорной информации о сообщении нет кроме его размера в N бит, то все возможные из 2^N вариантов считаются равновероятными и тогда неопределенность сообщения равна его размеру:

H(T) = -2^N·2^-N·log₂(2^-N) = N = | T |,

где через | X | обозначен размер блока данных X в битах. А если об исходном тексте неизвестно вообще ничего, даже его размер? В этом случае все равно необходимо принять за основу какую-либо модель распределения. Как правило, в реальности подобных трудностей не возникает, поскольку многие весьма стойкие шифры <не считают нужным> скрывать размер шифруемого сообщения, так как в этом действительно почти никогда нет особой необходимости, и эта характеристика априорно считается известной злоумышленнику. Там же, где этот размер все же реально необходимо скрыть, все сообщения перед зашифрованием преобразуются в массивы данных одной и той же длины, и мы опять получаем рассмотренную выше ситуацию.

После перехвата шифротекста эта величина, естественно, может измениться, теперь она становится апостериорной ("после-опытной") условной неопределенностью - условием здесь является перехваченное шифрованное сообщение T'. Теперь она задается следующей формулой:

,

где через p ( T_i | T' ) обозначена вероятность того, что исходное сообщение есть T_i при условии, что результат его зашифрования есть T'.

Одной из важнейших характеристик качества шифра служит количество информации об исходном тексте, которое злоумышленник может извлечь из перехваченного шифротекста - оно находится как разность между априорной и апостериорной неопределенностью исходного сообщения:

I = H(T ) - H(T | T' ).

Эта величина всегда неотрицательна. Показателем здесь является то, насколько уменьшится - понятно, что увеличиться она не может - неопределенность исходного текста при получении соответствующего шифротекста по сравнению с априорной неопределенностью, и не станет ли она меньше минимально допустимой величины.

В наилучшем для разработчиков шифра случае обе эти неопределенности равны:

H(T | T') = H(T),

то есть злоумышленник не может извлечь никакой полезной для себя информации об открытом тексте из перехваченного шифротекста: I = 0. Иными словами, знание шифротекста не позволяет уменьшить неопределенность соответствующего открытого текста, улучшить его оценку и увеличить вероятность его правильного определения. Шифры, удовлетворяющие данному условию, называются абсолютно стойкими или совершенными шифрами, так как зашифрованные с их применением сообщения не только не могут быть дешифрованы в принципе, но злоумышленник даже не сможет приблизиться к успешному определению исходного текста, то есть увеличить вероятность его правильного дешифрования.

Естественно, основной вопрос, который интересовал криптографов, это существуют ли на практике абсолютно стойкие шифры. Специалистам было интуитивно понятно, что они существуют, и пример подобного шифра привел Вернам более чем за два десятилетия до того, как один из основоположников теории информации К.Шеннон формально доказал их существование. В этом доказательстве Шеннон также получил и необходимое условие абсолютной стойкости шифра:

Для того, чтобы шифр был абсолютно стойким, необходимо, чтобы неопределенность алгоритма шифрования была не меньше неопределенности шифруемого сообщения:

Неопределенность алгоритма шифрования определяется точно так же, как и неопределенность сообщения - математическое ожидание двоичного логарифма вероятности использования алгоритма со знаком минус, - и имеет смысл только в том случае, если определено множество возможных алгоритмов и задана вероятность использования каждого из них. Стойкость шифров основана на секретности, то есть на неопределенности для злоумышленника алгоритма расшифрования - если бы это было не так, любой бы мог расшифровать зашифрованные данные. Чем меньше знает злоумышленник о шифре, тем менее вероятно успешное дешифрование сообщения. Поясним сказанное на примере: пусть перехвачена короткая 12-битовая шифровка, имеющая следующее содержание:

1 0 0 1 0 1 1 1 0 1 0 1

Для простоты предположим, что исходное сообщение имеет ту же длину. Если у злоумышленника нет никаких априорных сведений о зашифрованном сообщении, для него каждый из 2¹² исходных вариантов равновероятен, и, таким образом, вероятность правильно определить исходное сообщение простым угадыванием равна 2^-12. Предположим теперь, что злоумышленнику априорно известно, что зашифрование является наложением одной и той же 4-битовой маски на каждую 4-битовую группу сообщения с помощью операции побитового исключающего или. Очевидно, возможно 16 = 2⁴ различных вариантов битовой маски, соответственно, возможно 16 различных значений исходного текста:

маска исходный текст

0000 100101110101

0001 100001100100

0010 101101010110

.....

1111 011010001010

Таким образом, теперь вероятность правильно угадать исходный текст равна 1/16 - знание особенности использованного способа шифрования повысило ее в 256 раз. Отсюда следует интересный вывод: чем больше неопределенность в шифрующем преобразовании для постороннего лица, тем дальше оно стоит от разгадки шифра, тем шифр надежнее. Шифр, полностью неопределенный для злоумышленника

является нераскрываемым для него, то есть абсолютно стойким! Получается, что надежность шифра зависит исключительно от его секретности и не зависит от прочих его свойств.

Самое интересное, что это верно, и никакого парадокса здесь нет. Однако, на практике бывает сложно сохранить полную неопределенность относительно шифра у злоумышленника - он может получить информацию о шифре следующими способами:

- анализировать перехваченное шифрованное сообщение - практически всегда в его распоряжении имеется определенный набор шифротекстов, для некоторых из них могут иметься и соответствующие открытые тексты, или даже возможность получить шифротекст для любого наперед заданного открытого текста;

- злоумышленник может располагать априорными сведениями о шифре, полученными из различных источников - например, раньше это могла бы быть инструкция по шифрованию или черновик с промежуточными результатами для конкретного текста, в настоящее время - фрагмент компьютерного кода или микросхема, реализующая шифрование аппаратно.

Первая возможность есть у злоумышленника всегда, вторая также очень вероятна - трудно удержать в секрете от посторонних активно "работающий" алгоритм. Исходя из сказанного выше, можно перечислить несколько качеств, которым должен удовлетворять шифр, претендующий на то, чтобы считаться хорошим.

1. Анализ зашифрованных данных не должен давать злоумышленнику никаких сведений о внутреннем устройстве шифра. В шифротексте не должно прослеживаться никаких статистических закономерностей - например, статистические тесты не должны выявлять в зашифрованных данных никаких зависимостей и отклонений от равновероятного распределения битов (символов) шифротекста.

2. Алгоритм должен быть перенастраиваемым. В распоряжении злоумышленника рано или поздно может оказаться описание алгоритма, его программная или аппаратная реализация. Для того, чтобы в этом случае не пришлось заменять алгоритм полностью на всех узлах шифрования, где он используется, он должен содержать легко сменяемую часть.

Второе условие приводит нас к принципу Кирхгофа (в переводах с английского его иногда "обзывают" Керкхоффом, что не вполне верно, так как он голландец, а не англичанин, и транскрипция его фамилии должна быть немецкой, а не английской), безоговорочно принятому сейчас в искусстве построения надежных шифров. Этот принцип заключается в следующем: шифр определяется как параметризованный алгоритм, состоящий из процедурной части, то есть описания того, какие именно операции и в какой последовательности выполняются над шифруемыми данными, и параметров - различных элементов данных, используемых в преобразованиях. Раскрытие только процедурной части не должно приводить к увеличению вероятности успешного дешифрования сообщения злоумышленником выше допустимого предела. По этой причине, а также в силу того, что рассекречивание этой части достаточно вероятно само по себе, особого смысла хранить ее в секрете нет. В секрете держится некоторая часть параметров алгоритма, которая называется ключом шифра:

T' = E ( T ) = E_K ( T ),

здесь K - ключ шифра.

Использование принципа Кирхгофа позволяет получить следующие преимущества в построении шифров:

- разглашение конкретного шифра (алгоритма и ключа) не приводит к необходимости полной замены реализации всего алгоритма, достаточно заменить только скомпрометированный ключ;

- ключи можно отчуждать от остальных компонентов системы шифрования - хранить отдельно от реализации алгоритма в более надежном месте и загружать их в шифрователь только по мере необходимости и только на время выполнения шифрования - это значительно повышает надежность системы в целом;

- появляется возможность для точной оценки "степени неопределенности" алгоритма шифрования - она просто равна неопределенности используемого ключа:

H ( E_K ) = H ( K ).

Соответственно, становится возможным оценить вероятность и трудоемкость успешного дешифрования, то есть количество вычислительной работы, которую необходимо выполнить злоумышленнику для этого.

Вернемся к необходимому условию абсолютной стойкости шифра для шифров, построенных в соответствии с принципом Кирхгофа. В предположении, что никаких априорных данных о шифруемом тексте кроме его длины нет, получаем, что неопределенность исходного текста равна его длине, выраженной в битах:

H( T ) = | T |.

Максимально возможная неопределенность блока данных фиксированного размера достигается, когда все возможные значения этого блока равновероятны - в этом случае она равна размеру блока в битах. Таким образом, неопределенность ключа K не превышает его длины:

С учетом сказанного выше получаем необходимое условие абсолютной стойкости для шифров, удовлетворяющих принципу Кирхгофа:

Для того, чтобы шифр, построенный по принципу Кирхгофа, был абсолютно     стойким, необходимо, чтобы размер использованного для шифрования ключа    был не меньше размера шифруемых данных,

Точное равенство возможно только в том случае, если все возможные значения     ключа равновероятны, что эквивалентно условию, что биты ключа равновероятны    и статистически независимы друг от друга.

Примером абсолютно стойкого шифра может служить одноразовая гамма Вернама - наложение на открытые данные ( T ) ключа ( K ) такого же размера, составленного из статистически независимых битов, принимающих возможные значения с одинаковой вероятностью, с помощью некоторой бинарной операции ° :

T' = T ° K.

Используемая для наложения гаммы операция должна удовлетворять некоторым условиям, которые можно суммировать следующим образом: уравнение зашифрования должно быть однозначно разрешимо относительно открытых данных при известных зашифрованных и ключе, и однозначно разрешимо относительно ключа при известных открытых и зашифрованных данных. Если операция удовлетворяет этому свойству, она подходит. Среди подходящих операций нет подходящих лучше и подходящих хуже, с точки зрения стойкости шифра они все одинаковы - понятие "совершенство" не знает сравнительных степеней, оно либо есть, либо его нет. По указанной причине для практического использования обычно выбирают наиболее удобную в реализации операцию - побитовое суммирование по модулю 2 или побитовое исключающее ИЛИ, так как она:

- требует для своей реализации минимальной по сложности логики из всех возможных операций;

- обратна самой себе, поэтому для за- и расшифрования применяется одна и та же процедура.

Вернемся к вопросу об абсолютной стойкости шифров: как было отмечено ранее, абсолютно стойкие шифры требуют использования ключа, по размеру не меньшего шифруемых данных. Этот ключ должен быть и у отправителя, и у получателя, то есть его необходимо предварительно доставить им, а для этого необходим защищенный канал. Таким образом, наряду с потенциально незащищенным каналом для передачи зашифрованных данных необходимо существование защищенного канала для передачи такого же по размеру ключа. Это не всегда приемлемо по экономическим соображениям, поэтому подобные системы применяются лишь в исключительных случаях для защиты сведений, представляющих особую ценность. В подавляющем большинстве реальных систем шифрованной связи используются алгоритмы, не обладающие абсолютной стойкостью и поэтому называемые несовершенными шифрами.

Естественно, для таких шифров актуален вопрос надежной оценки их стойкости. Для них знание шифротекста позволяет снизить неопределенность соответствующего открытого текста, повысив тем самым вероятность успешного дешифрования. Однако, вопреки распространенному заблуждению, из этого вовсе не следует, что такое дешифрование возможно всегда.

Мнение о том, что сообщение, зашифрованное несовершенным шифром всегда можно однозначно дешифровать, если криптоаналитик располагает достаточным по объемы шифротекстом и неограниченными вычислительными возможностями, является чрезмерно грубым упрощением и в общем случае неверно.

Все дело в том, что несколько повысить вероятность успешного дешифрования и сделать ее равной единице - не одно и то же. Данную мысль легко проиллюстрировать на примере: пусть зашифрованию подвергается некий массив битов, ключ имеет размер один бит и шифрование осуществляется по следующим правилам:

- если ключ равен 0, инвертируются нечетные по номеру биты исходного текста, нумерация слева направо;

- если ключ равен 1, инвертируются четные по номеру биты исходного текста;

Таким образом, E₀(01) = 11, E₁(01) = 00. Очевидно, что наш шифр не обладает абсолютной стойкостью. Предположим, что перехвачена шифровка "10". Каков исходный текст? Понятно, что он может быть как 00 так и 11 в зависимости от значения ключа, и однозначно определить это невозможно, что и требовалось доказать. Для более серьезных шифров у криптоаналитика будет просто больше "вариантов выбора" открытого текста, и никаких указаний на то, какой из них предпочесть.

Таким образом, вопрос о возможности однозначного дешифрования сообщения, зашифрованного несовершенным шифром, остается открытым. Когда же такое дешифрование возможно? Шеннон в своих работах подробно исследовал этот вопрос. Для анализа он ввел в рассмотрение следующие характеристики шифра, в целях упрощения изложения здесь они приведены для варианта битового представления данных:

1. Функция ненадежности ключа - неопределенность ключа при известных n битах шифротекста:

f ( n ) = H( K | T' ), где | T' | = n.

Понятно, что f(n) может быть определена не для всех n.

2. Расстояние единственности шифра - такое значение n, при котором функция ненадежности, то есть неопределенность ключа становится близкой к 0.

U(E) = n, где n -минимальное из тех, для которых

Шеннон показал, что обе определенные выше величины зависят от избыточности открытого текста, причем расстояние единственности прямо пропорционально размеру ключа и обратно пропорционально избыточности:

,

где избыточность исходного текста R определяется следующим соотношением:

Сказанное означает, что полностью устранив избыточность открытого текста, мы сделаем невозможным его однозначное дешифрование на основе знания только соответствующего шифротекста, даже если в распоряжении криптоаналитика имеются неограниченные вычислительные возможности. При этом неопределенность исходного текста будет равной неопределенности, и, следовательно, размеру ключа:

H( T ) = H( K ) = | K |

Полное отсутствие избыточности в исходном тексте означает, что какой бы мы не взяли ключ, после расшифрования мы получим "корректные" исходные данные, и оснований предпочесть один вариант другому просто не будет. Из этого, в частности, следует, что в реальной практике перед зашифрованием данные весьма полезно "ужать" каким-либо архиватором. Конечно, полная безизбыточность исходного текста при этом недостижима, однако такое "ужатие" очень сильно затруднит криптоанализ на основе только шифротекста.

Аналогичные числовые характеристики стойкости шифра можно получить и для ситуации, когда в распоряжении криптоаналитика есть не только шифротекст, но и соответствующий открытый текст. Понятно, что они уже не будут зависеть от избыточности исходных сообщений. В этом случае расстояние единственности шифра имеет порядок размера его ключа, то есть весьма мало. В силу указанных причин такой шифр легко вскрывается при неограниченных вычислительных ресурсах аналитика, и при проектировании стойких шифров на первый план выступают уже совершенно другие принципы.

В большинстве практических случаев указанные условия выполняются, и для всех реальных шифров злоумышленник, располагающий неограниченными вычислительными ресурсами и шифротекстом достаточного размера, может однозначно дешифровать сообщение. Отсюда становится очевидным, что стойкость всех без исключения современных шифров, не являющихся совершенными, может базироваться только на вычислительной сложности дешифрования. Реально вычислительные возможности аналитика всегда ограничены и для них может быть получена верхняя оценка. Хорошо спроектированным считается шифр, который невозможно вскрыть с вычислительными затратами, осуществимыми за разумное время с запасом в несколько порядков даже с учетом прогнозируемого прогресса вычислительной техники.

В качестве меры трудоемкости раскрытия таких шифров обычно используют количество элементарных операций (w) некоторого типа, необходимых для дешифрования сообщения или определения ключа. Под элементарной операцией в различных случаях понимают разное, но обычно этим термином обозначают операцию, выполняемую на конкретной аппаратуре за один шаг ее работы - например, операцию типа "сложение", для универсальных процессоров, или цикл проверки одного ключа для специальных аппаратных схем перебора ключей. Трудоемкость дешифрования зависит от характера и количества информации, имеющийся в распоряжении аналитика. Обычно различают следующие виды криптоанализа:

- анализ на основе только шифротекста - у аналитика имеется только зашифрованное сообщение размером n:

w = W_GC(n);

- анализ на основе заданного открытого текста - аналитик располагает зашифрованным сообщением размером n и соответствующим ему открытым текстом:

w = W_GP(n);

- анализ на основе произвольно выбранного открытого текста - в распоряжении аналитика есть возможность получить результат зашифрования для произвольно выбранного им массива открытых данных размером n:

w = W_CP(n);

- анализ на основе произвольно выбранного шифротекста - в распоряжении аналитика есть возможность получить результат расшифрования для произвольно выбранного им зашифрованного сообщения размером n:

w = W_CC(n);

Предполагается, что криптоаналитик использует наилучший из доступных ему способов анализа. Конечно, последний вид криптоанализа несколько экзотичен, но, тем не менее, в соответствующих обстоятельствах и он возможен. Очевидно, что между величинами трудоемкости различных видов криптоанализа выполняются следующие соотношения:

Все рассмотренные характеристики трудоемкости имеют нижние границы:

w_xx = inf W_XX(n).

Очевидно также, что эти границы достигаются при некоторых конечных значениях параметра n, потому что при его неограниченном увеличении трудоемкость анализа, принимающего во внимание все имеющиеся в наличии данные, будет неограниченно возрастать:

w_xx = W_XX(n_xx).

Таким образом, для каждого вида криптоанализа (XX) существует свой оптимальный объем необходимых данных (n_xx), при возрастании объема имеющихся данных от нуля до этого значения трудоемкость анализа снижается до своего граничного значения (w_xx), а при дальнейшем возрастании - увеличивается. Эти критические объемы данных и соответствующие величины трудоемкости анализа и представляют особый интерес для специалистов-криптографов. Понятно, что реально трудоемкость анализа зависит не только от объема анализируемых данных, но и от самих этих данных. По этой причине все приведенные выше соотношения являются оценочными, а соответствующие величины считаются заданными с точностью до порядка-двух.

Следует различать точное значение показателей трудоемкости каждого вида анализа W_XX(n) и его текущую оценку , основанную на достижениях современного криптоанализа - понятно, что оценка больше оцениваемой величины:

и с развитием криптоанализа она постоянно снижается. Истинный интерес конечно же представляет сама оцениваемая величина. Однако, как отметил еще Шеннон, не существует способа получить точное значение трудоемкости анализа, все оценки базируются на проверках устойчивости шифров к известным на текущий момент видам криптоанализа, и нет гарантии, что в ближайшем или более отдаленном будущем не будут разработаны новые методы анализа, существенно ее снижающие.

Сказанное выше означает, что при текущем положении дел в криптографии стойкость абсолютно всех шифров, что за исключением совершенных, не может быть доказательно обоснована. Вместо этого она обосновывается эмпирически как устойчивость к известным на сегодняшний день видам криптоанализа, но никто не может дать гарантии того, что завтра не будет изобретен вид криптоанализа, успешный именно для данного конкретного шифра. Вот почему не стоит доверять "новейшим шифрам" - они не прошли проверку временем. По этой же самой причинам не является разумным доверять криптоалгоритмам, которые держатся их авторами в секрете - даже при отсутствии злонамеренно оставленных там "люков" нет совершенно никакой гарантии того, что алгоритм был исследован со всей необходимой тщательностью.

Сказанное не означает, что использование секретных алгоритмов шифрования вовсе лишено смысла. Оно является допустимым и разумным при выполнении двух следующих условий:

- между разработчиками и пользователями алгоритма существует уровень доверия, исключающий намерение разработчика нанести ущерб пользователю, предоставив ему недостаточно качественный шифр или шифр с оставленными в нем люками;

- специалисты, разработавшие алгоритм, имеют достаточно высокий уровень компетентности в этой области;

Указанные условия выполняются, например, для спецслужб ведущих государств, разрабатывающих для "внутреннего потребления" собственные шифры.

Рассмотрение следующей нашей темы - классификации шифров - начнем с двух требований, предъявляемых к практическим алгоритмам шифрования - они, в общем-то, естественны и понятны:

- шифр должен быть технически применим для закрытия массивов данных произвольного объема;

- шифр должен быть реализуем в виде устройства, имеющего ограниченный объем памяти, и его реализация должна быть эффективна при этом.

Попытка совместить оба требования неизбежно приводит к криптоалгоритму, в котором шифрование производится пошагово, порциями - массив данных разбивается на блоки ограниченного размера, и за один шаг шифруется один блок:

T = (T₁, T₂,..., T_n),

для всех i от 1 до n , где N-максимальный размер блока.

От размера шифруемого массива данных в этом случае зависит только количество шагов шифрования, но не сами шаги. Ради удобства реализации размер блока практически всегда полагают постоянным - может быть, за исключением последнего блока данных, который может быть меньше:

По соображениям стойкости размер блока не должен значительно превышать размер ключа, лучше, если он будет меньше или равен ему.

Существуют два принципиально различающихся подхода к построению шифров с секретным ключом, соответственно им можно выделить два типа шифров - блочные и потоковые шифры:

1. В блочных шифрах результат зашифрования очередного блока зависит только от него самого и не зависит от других блоков шифруемого массива данных:

T_i' = E(T_i).

Из этого следует, что в результате зашифрования двух одинаковых блоков открытого текста всегда получаются идентичные блоки шифротекста:

2. В поточных или потоковых шифрах результат зашифрования очередного блока зависит от него самого и, в общем случае, от всех предыдущих блоков массива данных:

T_i' = E(T₁, T₂,..., T_i).

Сюда же относится важный частный случай, когда результат зашифрования очередного блока зависит этого блока и от его номера:

T_i' = E(i,T_i).

По поводу разделения шифров на блочные и потоковые следует добавить, что в современной криптологии указанные понятия иногда используются в близком, но несколько отличном от сказанного выше смысле - потоковыми называют только такие шифры, в которых шифруемый за один шаг блок имеет размер один бит или один символ текста, а шифры с большим размером блока, формально относящиеся к потоковым, причисляют к блочным. Потоковые в последнем, практическом значении этого термина, шифры очень хорошо подходят для засекречивания асинхронного информационного потока - поступившая порция данных может быть немедленно зашифрована и отправлена в канал связи, нет необходимости ждать, пока наберется полный блок из нескольких битов или символов, как это было бы необходимо для блочных в том же самом "практическом" смысле термина шифров.

Если принять во внимание требование к реализуемости криптоалгоритма устройством с конечным числом возможных состояний, то наиболее общей моделью потоковых шифров является конечный автомат, описываемый множеством состояний X, входным и выходным алфавитами I и E, и правилами перехода и выхода и соответственно:

где для всех

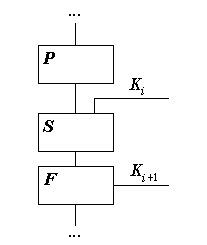
Множество состояний и алфавиты автомата являются конечными - собственно, именно поэтому автомат и называется конечным, - а правила перехода и выхода могут быть записаны в виде двумерной таблицы, и по этой причине иногда называются таблицами переходов и выходов соответственно. Автомат работает следующим образом: каждый символ, поступивший на его вход, вызывает изменение состояния автомата и порождение одного выходного символа. В результате входное слово преобразуется в слово точно такой же длины, составленное из символов выходного алфавита. Работа конечного автомата зависит от его начального состояния: в общем случае два идентичных автомата преобразуют одно и то же входное слово в разные выходные, если начнут свою работу с разных состояний.

Для того, чтобы процедура шифрования была обратима, для шифрующего автомата должен существовать обратный ему автомат. Один конечный автомат является обратным другому и называется его обращением в том случае, если он преобразует любую выходную последовательность этого автомата в его входную последовательности. На рисунке 1 второй конечный автомат (правый, DFA) преобразует выходную последовательность s₁s₂...s_K первого конечного автомата (левый, EFA) в его входную последовательность t₁t₂...t_K, и в силу этого является его обращением.

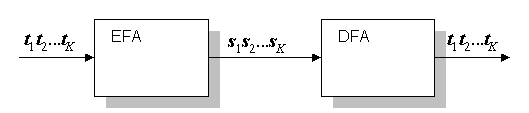
Конечный автомат и его обращение.

Так как работа конечного автомата зависит от его начального состояния, то для каждого допустимого начального состояния автомата должно существовать парное ему начальное состояние его обращения, при котором эти автоматы, соединенные в каскад как показано на рисунке 1, работают как тривиальный автомат, выдающий без изменения на выход все то, что поступило ему на вход. Отсюда следует, что для корректного расшифрования выполняющий эту процедуру автомат должен быть синхронизирован с шифрующим - он должен начать свою работу с состояния, парного начальному состоянию последнего, для чего ему необходима информация об этом состоянии. Эта информация называется синхропосылкой и передается до начала передачи зашифрованных данных всякий раз при установлении или восстановлении соединения после сбоя в канале связи. По вполне понятной причине синхропосылка может передаваться только в открытом виде - на момент ее получения автомат расшифрования на принимающей стороне не готов к работе.

В настоящее время одним из наиболее популярных видов потоковых шифров является шифр гаммирования, в котором соответствующий конечный автомат является безвходовым и используется для выработки последовательности элементов гаммы:

Для наложения гаммы на данные может быть использована любая подходящая бинарная операция. Если это операция аддитивного типа, шифр называется аддитивным, если же используется операция побитового сложения по модулю 2 - то двоичным аддитивным. Как мы с вами выяснили в предыдущем выпуске, с точки зрения надежности шифра все допустимые операции наложения гаммы одинаковы, по этой причине в реальных шифрах используют наиболее просто реализуемую их них. Для двоичных данных таковой является операция побитового суммирования по модулю 2 или побитового исключающего ИЛИ:

Кроме того, эта операция является обратной самой себе и по этой причине может использоваться как для зашифрования, так и для расшифрования данных, что позволяет реализовать обе эти процедуры в одном модуле, достигнув тем самым дополнительных преимуществ в экономичности.

Условием стойкости шифра гаммирования является невозможность определить по известному фрагменту гаммы другие ее части или восстановить структуру порождающего ее конечного автомата. Для стороннего наблюдателя, обладающего лишь ограниченными вычислительными возможностями, выработанная гамма должна быть неотличима от случайной последовательности. В заключение рассмотрения темы потоковых шифров отметим, что эта область криптографии целиком базируется на теории конечных автоматов - очень подробно разработанной на сегодняшний день отрасли математики, и по этой причине считается одним из наиболее полно исследованных разделов криптологии. Теперь перейдем к рассмотрению блочных шифров - именно они станут темой нескольких ближайших выпусков. В шифрах этого типа результат зашифрования каждого блока зависит только от его значения, естественно, не считая секретного ключа:

T_i' = E_K(T_i).

Как следствие, при зашифровании двух одинаковых блоков данных получатся идентичные блоки шифротекста:

Из указанной особенности блочных шифров следует очевидный способ их анализа - статистический. Если известен закон распределения блоков открытого текста, то проанализировав статистику блоков шифротекста, можно установить соответствие между ними. Классическим примером такого криптоанализа является история, описанная Эдгаром По в его известном рассказе "Золотой жук". Для того, чтобы исключить подобную возможность, размер блока должен быть выбран достаточно большим. Например, при размере блока в один байт анализ шифра осуществим вручную, без использования вычислительной техники; при размере блока в 16 бит этот анализ элементарно реализуется на персональной ЭВМ и занимает несколько секунд; при размере блока в 32 бита компьютерный анализ также осуществим, хотя требует больше времени и большего необходимого объема зашифрованных данных. При дальнейшем увеличении размера блока статистический анализ становится все менее осуществимым на практике. Для большинства современных шифров выбрана величина блока в 64 бита, для нее исчерпывающий анализ практически исключен прежде всего из-за невозможности набрать соответствующую статистику шифротекстов. При еще больших размерах блока усложняется не только криптоанализ, усложняется и сам алгоритм шифрования - вот почему неразумно увеличивать его сверх необходимого. Как мы увидим в следующем выпуске, для шифров очень распространенной на сегодняшний день архитектуры, называемой "сбалансированная сеть Файстеля" (balanced Feistel network) условием эффективной реализации в виде программы для ЭВМ является равенство половинного размера блока криптоалгоритма величине машинного слова. Именно поэтому реализация отечественного стандарта шифрования - алгоритма ГОСТ 28147-89, шифра с 64-битовым размером блока, - для 32-битовых процессоров Intel x86 существенно эффективнее реализации этого же алгоритма для 16-битовых процессоров той же серии - естественно, сравнение производилось на одном и том же компьютере. В настоящее время подавляющее количество компьютеров в мире - 32 битовые, и по этой причине выбирать размер блока для упомянутой архитектуры шифров больше 64 бит совершенно бессмысленно, а с точки зрения эффективности реализации - вредно. Хотя для блочных шифров с достаточно большим размером блока провести исчерпывающий статистический анализ в общем случае невозможно, тем не менее, анализируя зашифрованные данные, легко обнаружить наличие одинаковых блоков в исходных данных, что позволяет выявить стабильные паттерны, имеющиеся в них. Предположим, например, что целиком шифруется магнитный диск с информацией. На таком диске все незанятое пространство обычно заполнено фиксированными кодами, записанными туда при его форматировании. После шифрования на месте этого кода получатся одинаковые блоки шифротекста, что позволит злоумышленнику отличить незанятое пространство диска от пространства, заполненного полезными данными. Иногда это бывает неприемлемым, поэтому перед зашифрованием данных их очень полезно сжимать архиваторами, что существенно снижает избыточность данных и уменьшает вероятность встретить повторяющиеся блоки. В тех случаях, когда данные имеют физическую привязку - как в приведенном примере с шифрованием диска - их рекомендуется рандомизировать - модифицировать с использованием случайных или псевдослучайных.

Каким же условиям должен удовлетворять стойкий блочный шифр? Эти условия сформулировал Шеннон в ряде своих основополагающих работ по теории шифрования: такой шифр должен обладать свойствами перемешивания и рассеивания:

- рассеивание: это свойство шифра, при котором один символ (бит) исходного текста влияет на несколько символов (битов) шифротекста, оптимально - на все символы в пределах одного блока. Если данное условие выполняется, то при шифровании двух блоков данных с минимальными отличиями между ними должны получаться совершенно непохожие друг на друга блоки шифротекста. Точно такая же картина должна иметь место и для зависимости шифротекста от ключа - один символ (бит) ключа должен влиять на несколько символов (битов) шифротекста.

- перемешивание: это свойство шифра скрывать зависимости между символами исходного текста и шифротекста. Если шифр достаточно хорошо "перемешивает" биты исходного текста, то соответствующий шифротекст не содержит никаких статистических, и, тем более, функциональных закономерностей - опять же, для стороннего наблюдателя, обладающего лишь ограниченными вычислительными ресурсами.

Если шифр обладает обоими указанными свойствами в достаточной степени, то любые изменения в блоке открытых данных приводят к тому, что с точки зрения наблюдателя все символы (биты) в зашифрованном блоке получат новые значения, равновероятные в области их определения и независимые друг от друга. Так, если шифр оперирует информацией, представленной в двоичной форме, то инвертирование даже одного бита в блоке исходных данных приведет к тому, что все биты в соответствующем блоке шифрованных данных с вероятностью 1/2 независимо друг от друга так же поменяют свое значение. Такой шифр невозможно вскрыть способом, менее затратным с точки зрения количества необходимых операций, чем полный перебор по множеству возможных значений ключа. Данное условие является обязательным для шифра рассматриваемого типа, претендующего на то, чтобы считаться хорошим.

Как же создать надежный шифр, соответствующий всем приведенным выше условиям надежности? Шеннон предложил строить его из простых шифров, как большой дом строится из отдельных кирпичиков. Каждый из использованных простых шифров может не обладать рассмотренными выше свойствами, но все вместе они образуют вполне стойкий шифр.

В настоящем выпуске мы с вами начнем рассмотрение архитектуры блочных шифров, безоговорочно доминирующей в традиционной криптографии на нынешнем этапе ее развития. Из предыдущих выпусков нам стало известно, что сильный блочный шифр должен обладать свойствами рассеивания и перемешивания, и что главная идея в построении таких шифров - использование последовательности большого числа простых шифрующих преобразований. Поэтому настоящий выпуск начнем с рассмотрения этих преобразований - основных строительных кирпичиков серьезных шифров.

Под простым шифрующим преобразованием здесь и далее понимается такое преобразование, который реализуется аппаратно относительно несложной логической схемой или программно несколькими компьютерными командами. Можно выделить следующие группы простых шифров:

- шифр перестановок - заключается в перестановках структурных элементов шифруемого блока данных - битов, символов, цифр;

- шифр замен - заключается в замене одних значений на другие по индексной таблице, замене подвергаются группы элементов шифруемого блока - битов или символов;

- шифр функциональных преобразований - заключается в выполнении сдвигов, логических и арифметических операций над элементами данных.

Ниже дана подробная характеристика каждого из упомянутых типов преобразований:

Шифры перестановок чрезвычайно просто реализуются аппаратно - разводкой проводников на плате или в кристалле, при этом совсем не требуется каких-либо дополнительных затрат, так как проводники, связывающие регистры аппаратуры, так или иначе присутствуют в схеме. В то же самое время эти преобразования очень неэффективно реализуются программно на процессорах общего назначения. Как правило, вычислительные затраты составляют не менее двух машинных команд на каждый двоичный разряд в модифицируемом блоке, если только в перестановках нет согласованности. Этой причиной, в частности, объясняется тот факт, что многие шифры, широко использующие операции данного типа, имеют при прочих равных условиях существенно менее эффективные реализации по сравнению с шифрами, их не использующими. Например, американский стандарт шифрования криптоалгоритм DES при вдвое меньшем количестве шагов в цикле шифрования по сравнению с Российским стандартом (16 против 32) имеет примерно вдвое более медленную оптимальную реализацию для процессоров Intel x86.

Общие виды замен аппаратно реализуются с помощью запоминающих устройств, программно - индексированным чтением из оперативной памяти, что, по сути, одно и то же: замена для элемента данных x берется из вектора или узла замен V, являющегося массивом заменяющих значений, индексированным заменяемым элементом данных:

x заменяется на y = V [x].

Программно такая операция реализуется за одну команду, не считая операции загрузки индекса в соответствующий регистр. Размер памяти, необходимый для хранения вектора заменяющих, определяется следующим соотношением:

|V | = 2^|X|·|Y |,

где |X | и |Y | - размеры заменяемого и заменяющего блоков в битах соответственно, размер вектора замен V также получается в битах. Из приведенной формулы видно, что он растет экспоненциально с ростом размера заменяемого блока. В силу этого выполнение подстановки в масштабах всего шифруемого блока на невозможно - потребовался бы слишком большой объем памяти для хранения вектора. Поэтому преобразуемый блок данных разделяют на фрагменты, обычно одинакового размера, и выполняют замену в этих подблоках независимо друг от друга. Для повышения стойкости шифра замену различных частей шифруемого блока следует выполнять с использованием разных векторов замен, которые все вместе составляют таблицу подстановок или таблицу замен. Для хранения этой таблицы требуется участок памяти следующего размера:

|S  | = n_v|V  | = n_v·2^|X|·|Y  |,

где n_v - число подблоков размера |X |, в которых производятся подстановки. Как уже отмечалось выше, размер таблицы подстановок быстро увеличивается с ростом размера заменяющего, и, особенно, заменяемого блока, что влечет за собой возрастание требований к необходимому для реализации шифра объему памяти. С другой стороны, увеличение этих размеров усложняет криптоанализ и, тем самым, повышает стойкость шифра, поэтому на практике их следует выбирать на границе разумности, ведь криптоалгоритм проектируется на достаточно длительный срок, а возможности электронной техники увеличиваются очень быстро. В алгоритме DES суммарный объем блоков подстановки равен |S_DES| = 8·2⁶·4 = 2¹¹ бит = 256 байт. В отечественном стандарте это величина того же порядка: |S_ГОСТ| = 8·2⁴·4 = 2⁹ бит = 64 байта. Следует помнить, что указанные шифры разрабатывались в семидесятые годы, когда понятие "микросхема" еще только начинало входить в наш обиход, обычная емкость микросхемы запоминающего устройства составляла несколько десятков, максимум сотен битов, а объем оперативной памяти 32Кбайта считался совсем неплохим вариантом для компьютера. Вполне естественно, что созданные в то время криптоалгоритмы отражали суровые реалии тех дней. Сейчас эта проблема практически отсутствует, и поэтому современные шифры гораздо более свободны в данном отношении. Так, в криптоалгоритме BLOWFISH подстановки производятся следующим образом: каждый из 4-х байтов, составляющих 32-битовое слово, заменяется на 4-байтовое слово, полученные слова преобразуются в одно с помощью логических и арифметических операций. Соответственно размер одной таблицы замен в этом алгоритме равен |S_BLOWFISH| = 4·2⁸·32 = 2¹⁵ бит = 4 Кбайт.

Фрагмент составного шифра - комбинация большого числа элементарных шифрующих преобразований.

Функциональные преобразования - это унарные и бинарные логические и арифметические операции, реализуемые аппаратно логическими схемами, а программно -одной-двумя компьютерными командами. Теоретически, возможно использовать любую операцию, которая может быть сформулирована в терминах логических функций. Однако на практике дело всегда ограничивается теми из них, которые имеются в наборах команд универсальных процессоров и реализованы аппаратно в виде микросхем. Из логических операций это основные логические функции - инверсия, и бинарные - побитовые И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, из арифметических - изменение знака (переход к дополнительному коду), и бинарные - сложение, вычитание, умножение, деление по модулю некоторого числа, из битовых манипуляций - циклические сдвиги.

Как же построить надежный шифр из элементарных операций указанного типа? Наиболее очевидная идея - каскадировать их, как это показано на рисунке 1. Символами P, S, F на нем обозначены операции перестановок (Permutation), замен (Substitution), функциональных преобразований (Function) соответственно. Ключевые элементы (K_i) могут комбинироваться с преобразуемыми данными в операциях подстановок и функциональных преобразований.

Не имеет смысла комбинировать две однотипные операции подряд. Если чередовать процедуры различного типа, сложность результирующего преобразования (степень перемешивания и рассеивания) будет выше. Это очень легко объяснить: при комбинировании двух операций их сложности складываются за вычетом некоего "дефекта сложности", который тем больше, чем более схожи две операции. Например, суперпозиция (результат последовательного выполнения) двух битовых перестановок может быть выражен одной перестановкой. То же справедливо для двух подстановок, выполняемых в одних и тех же границах заменяемых подблоков. Прибавление к блоку данных двух ключевых элементов равносильно прибавлению одного, равного их сумме. Во всех рассмотренных случая добавление к операции еще одной такой же вообще не приводит к возрастанию сложности, а следовательно и стойкости преобразования.

Даже если комбинируются две различные операции, принадлежащие одной и той же группе, сложность полученного преобразования меньше, чем могла бы быть, если бы они были разделены операцией другого типа. На рисунке 2 изображены два трехзвенных шифрующих преобразования, составленных из одних и тех же операций. Сложность и стойкость преобразования, изображенного справа, по только что изложенным соображениям выше, чем у левого.

Пара шифрующих преобразований из трех элементарных операций, использованных в различном порядке

Каким же условиям должен удовлетворять шифр, не только обладающий необходимой стойкостью, но, в добавок к этому удобный в реализации и использовании. Рассмотрение начнем с требований, которые были особенно актуальными четверть века назад, когда возможности микроэлектронных приборов были весьма ограничены и соображения экономичности и самой возможности реализации шифров на имеющейся элементной базе играли определяющую роль. Сейчас их актуальность заметно меньше, но, тем не менее, они остаются в достаточной степени важными для того, чтобы учитываться и в современных разработках.

1. Операции за- и расшифрования должны быть близкими настолько, чтобы могли быть выполнены одним и тем же аппаратным или программным модулем - это диктуется требованием экономичности реализации.

2. Объем ключевой информации должен быть относительно небольшим. Разумным является такой размер ключа, при котором невозможно его нахождение путем перебора по всему ключевому пространству, с определенным запасом на возможный прогресс электронной техники. В настоящее время граница практической осуществимости подбора ключа находится где-то в районе 60-64 бит. Соответственно, разумным может считаться размер ключа 80-256 бит. Данное требование вытекает из необходимости хранить ключи на любых носителях, включая нетрадиционные, например - на персональных миниатюрных магнитных карточках.

3. Реализация шифра (код программы и постоянные данные) должна быть достаточно компактной для того, чтобы "уместиться" на микроконтроллерах с относительно невысоким объемом запоминающего устройства - последнее требование также диктуется соображениями экономичности реализации.

Рассмотрим, каким образом можно построить шифр, удовлетворяющий указанным требованиям. Начнем с условия обратимости процедуры зашифрования. Из него вытекает, что все преобразования, непосредственно модифицирующие шифруемые данные, должны быть обратимыми, то есть при их выполнении не должна теряться информация. Перестановка обратима по определению. Непараметризованная замена имеет обратную операцию если она сюрьективна, то есть если каждое возможное заменяющее значение встречается в соответствующем векторе замен ровно один раз. Параметризованная, то есть зависящая от значения ключевого элемента, замена обратима в том случае, если при каждом фиксированном значении параметра соответствующая простая замена обратима. Бинарная функциональная операция обратима, если при каждом фиксированном значении второго, модифицирующего, аргумента задаваемое ей отображение сюрьективно, это равносильно условию, что уравнение модификации элемента данных Y = f (X,K) всегда однозначно разрешимо относительно модифицируемого элемента (X). Унарные функциональные операции можно рассматривать как некоторые бинарные с фиксированным вторым операндом. Из простых обратимых унарных и бинарных логических операций над числами конечной разрядности следует отметить инверсию и операцию побитового исключающего или, из арифметических - изменение знака числа, сложение или вычитание в пределах разрядной сетки числа, умножение и деление по модулю простого числа. Если шифрующее преобразование определено как цепочка описанных выше элементарных операций, то достаточно просто построить обратное ему, если только все элементарные операции в цепочке обратимы.

Для этого достаточно выполнить перечисленные ниже требования, которые, хотя и не являются абсолютно необходимыми, тем не менее исчерпывают практически все случаи эффективно реализуемых преобразований, и потому на практике всегда принимаются во внимание:

1. Все шифрующие преобразования должны принимать на входе и выдавать на выходе блок данных одного и того же размера, не считая дополнительных входов для параметра замены и второго операнда функционального преобразования.

2. Замены, применяемые непосредственно к шифруемым данным, должны быть обратимыми, параметризованные замены должны быть обратимыми при каждом фиксированном значении параметра.

3. Уравнение функционального преобразования шифруемых данных с помощью бинарной операции должно быть всегда однозначно разрешимо относительно преобразуемого (первого) операнда.

В этом случае для составного шифрующего преобразования, имеющего линейную структуру, можно очевидным образом сконструировать обратное преобразование: оно строится комбинированием обращений его составных частей в порядке, обратном тому, в котором они использовались в исходном преобразовании, как это показано на рисунке 3.

Если прямое преобразование определяется формулой

,

то обратное ему преобразование задается следующей формулой:

В данных формулах обозначает одну из перечисленных выше простых операций преобразования (перестановку, подстановку или функциональную операцию), возможно, зависящую от параметра - ключевого элемента K_i. Операции группируются справа налево, то есть (T₂T₁)(X) обозначает T₂(T₁(X)).

Шифрующее преобразование с линейной структурой и обратное ему шифрующее преобразование.

Для того, чтобы прямое и обратное преобразование было возможно реализовать в одном аппаратном блоке или программном модуле, они должны быть идентичны с точностью до используемых ключевых элементов. Это означает, что шифрующее преобразование должно быть "антисимметрично" самому себе - для каждого его шага, находящегося на определенном расстоянии от начала преобразования, на точно таком же расстоянии от его конца должен располагаться обратный ему шаг, использующий тот же самый ключевой элемент:

T ^-1 ~ T,

если для всех i справедливо следующее условие:

, для всех K_i, или

Если данное условие выполняется, процедуры за- и расшифрования могут осуществляться одним и тем же программным и аппаратным модулем и отличаются только порядком использования ключевых элементов.

Теперь рассмотрим требование относительного небольшого размера ключа - как было отмечено выше, он не должен быть намного больше размера, достаточного для исключения практической возможности его нахождения полным перебором по всему ключевому пространству. Так как этот "критический" размер составляет в настоящее время величину порядка восьми байт, разумный размер ключа не превышает 256 бит. Ясно, что для получения необходимой стойкости шифра придется использовать достаточно большое количество элементарных шагов преобразования, нуждающихся в наборе ключевых элементов, намного (в разы) превосходящем по размеру ключ. Поэтому во всех шифрах подобного типа применяется процедура "развертывания", с помощью которой из небольшого ключа строится массив ключевых элементов нужного размера.

Процедура "развертывания" ключа должна удовлетворять следующим требованиям:

1. Биты (символы) каждого ключевого элемента должны быть равновероятны и статистически независимы друг от друга.

2. Биты (символы) каждого ключевого элемента должны быть статистически независимы от битов (символов) нескольких соседних ключевых элементов. Это условие должно выполняться в пределах такого количества шагов шифрования, на котором еще можно проследить статистические зависимости между битами (символами) шифруемых блоков.

Шаги шифрующего преобразования

Данное требование проиллюстрировано на рисунке 4. Для любой пары шагов шифрующего образования, не обязательно смежных, допускается тем меньшая коррелированность используемых ими ключевых элементов, чем больше коррелированность выхода первого из них со входом второго:

где С - некоторая мера коррелированности. Понятно, что данная зависимость не является количественно строгой, она отражает суть вопроса лишь качественно. Опять же следует отметить, что данное требование не является абсолютно необходимым. Нет ничего страшного, если оно выполняется не в полной мере для отдельных пар шагов преобразования. Однако систематическое игнорирование этого правила приводит к тому, что криптоанализ шифра значительно облегчается.

Криптостойкость последовательности ключевых элементов является необязательным, но весьма полезным ее свойством, так как сама по себе гарантирует выполнение двух вышеприведенных требований. Возможны различные подходы к выработке ключевых элементов для шагов шифрования - от самых простых, до обладающих сложностью, сопоставимой со сложностью самого шифра. Например, в качестве ключевых элементов для шагов шифрования можно просто брать фрагменты ключа, как это делается в отечественном стандарте шифрования. Можно вырабатывать ключевые элементы с помощью генератора псевдослучайных чисел. Здесь спектр возможных решений чрезвычайно широк - от сравнительно несложных схем выработки гаммы на основе сдвиговых регистров с обратной связью до генерации последовательности элементов с помощью того же самого криптоалгоритма. Последний подход реализован, например, в шифре BLOWFISH. Конечно, он значительно увеличивает стойкость шифра, но и существенно затрудняет его эффективную реализацию. Например, в упомянутом шифре BLOWFISH построение массива ключевых элементов вычислительно эквивалентно выполнению более 500 циклов шифрования, что делает его непригодным для реального практического использования всюду за исключением систем, в которых смена ключа происходит достаточно редко, и объемы массивов, шифруемых на одном ключе, велики.

Наконец, требование компактности реализации алгоритма с точки зрения кода и используемых постоянных данных приводит к идеологии его построения из одинаковых групп преобразований, повторенных нужное число раз. В этом случае реализация алгоритма работает итеративно - результат каждой итерации, за исключением последней, является входом для следующей итерации. Кроме того, очевидно, что каждая повторяющаяся группа преобразований, из которых построен криптоалгоритм, должна удовлетворять рассмотренному выше требованию антисимметричности прямого и обратного криптопреобразований, которое в данном случае должно выполняться на уровне отдельных групп.

Требование компактности вспомогательных массивов данных можно выполнить, используя на разных итерациях преобразования один и тот же комплекта векторов замен.

Таким образом, в настоящем выпуске мы с вами рассмотрели базовые требования, в соответствии с которыми строятся современные шифры:

- построение шифров из простых преобразований - перестановок, подстановок, элементарных функциональных операций и чередование операций различного типа;

- циклическая, итеративная структура алгоритма - одна итерация состоит из нескольких простых преобразований, итерации отличаются друг от друга только использованными ключевыми элементами;

- антисимметричная структура алгоритма, позволяющая достичь структурной эквивалентности процедур за- и расшифрования, они отличаются друг от друга только последовательностью использования ключевых элементов;

- использование ключа относительно небольшого размера и выработка из него массива ключевых элементов для шагов преобразования с помощью процедуры "развертывания" ключа.