Лекция 10. Обработка двумерных массивов

10.1. Ввод и вывод двумерного массива

В двумерном массиве, матрице, элементы представлены в табличном виде. Доступ к элементу матрицы осуществляется по общему имени и двум индексам – номеру строки (i) и номеру столбца (j). Эти номера определяют расположение элемента в матрице. Размерность матрицы определяется как M*N, где M – количество строк матрицы, а N – количество столбцов. Каждая строка матрицы и каждый столбец представляют собой одномерный массив.

Ниже приведена матрица A(3x4).

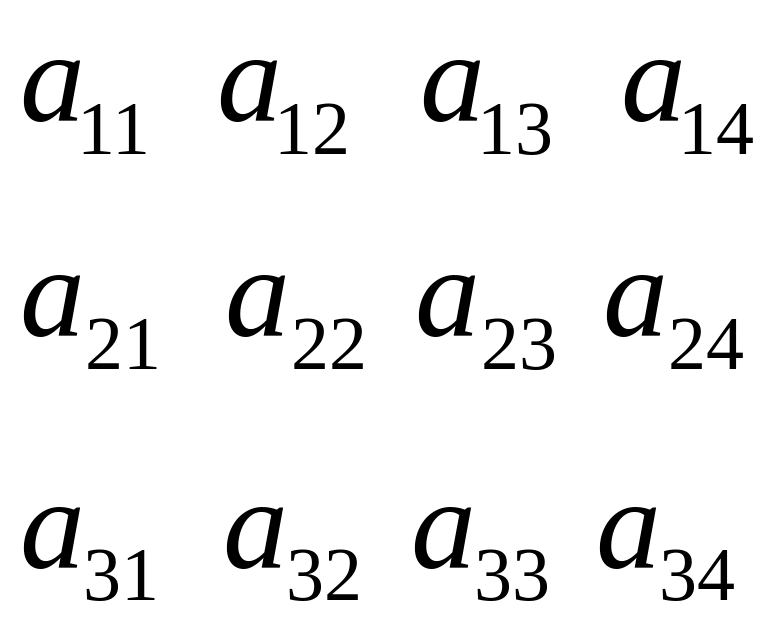
Матрица вводится и выводится построчно. А каждая строка вводится и выводится поэлементно.

Рассмотрим порядок поэлементного ввода матрицы 3x4. Пусть i – номер строки, а j – номер столбца.

Ввод элементов 1-ой строки:

i=1

j=1 ввод a₁₁

j=2 ввод a₁₂

j=3 ввод a₁₃

j=4 ввод a₁₄

После того, как элементы 1-ой строки введены, переходим ко 2-ой строке:

i=2

j=1 ввод a₂₁

j=2 ввод a₂₂

j=3 ввод a₂₃

j=4 ввод a₂₄

Ввод элементов 3-ей строки:

i=3

j=1 ввод a₃₁

j=2 ввод a₃₂

j=3 ввод a₃₃

j=4 ввод a₃₄

Очевидно, что ввод, вывод и обработка матрицы должны осуществляться в цикле и не в простом, а во вложенном.

Блок-схема алгоритма ввода матрицы приведена на рис. 10.1. Как видно ввод осуществляется в 2 этапа:

1. вводится размерность матрицы : M, N;

2. организуется вложенный цикл для построчного ввода матрицы, причем каждая строка вводится поэлементно.

Рис. 10.1. Построчный ввод матрицы

Алгоритм вывода матрицы аналогичен вводу.

2. Обработка двумерного массива

Матрица может обрабатываться как построчно, так и по столбцам. Зависит это от поставленной задачи. Рассмотрим несколько алгоритмов обработки матрицы.

ПРИМЕР 10.1. Задана матрица X(N*N). Определить сумму ее элементов, расположенных выше главной диагонали, и произведение элементов ниже главной диагонали. Алгоритм решения приведен на рис. 10.2. Как видно обработка заданной матрицы X происходит построчно:

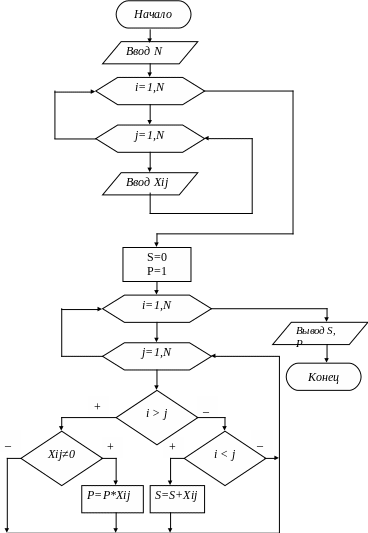
Рис. 10.2

Рис. 3.40. Алгоритм решения примера 3.26

i –

номер строки матрицы и параметр внешнего цикла; j – номер столбца и параметр внутреннего цикла.

ПРИМЕР 10.2. Задана матрица A(MxN). Сформировать вектор G(M), каждый элемент которого равен количеству отрицательных элементов в соответствующей строке матрицы. Т.е. G1 равен количеству отрицательных элементов в 1-ой строке, G2 - количеству отрицательных элементов во 2-ой строке, и т.д. Т.к. перебирать и анализировать элементы необходимо в каждой строке, то обработку матрицы следует организовать построчно.

Алгоритм решения приведен на рис. 10.3

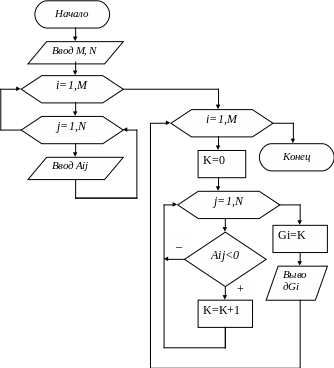
Рис. 10.3. Алгоритм решения примера 10.2.

Здесь для каждой строки организован перебор элементов и накопление счетчика количества отрицательных элементов К. Перед перебором элементов каждой строки счетчик K очищается. Когда перебор элементов i-ой строки завершен, определяется и выводится i-ый элемент массива G (Gi=K). Затем i увеличивается на 1, вновь очищается счетчик K и начинается перебор элементов следующей строки и т.д.. Вектор G будет сформирован окончательно (т.е. все его элементы будут определены) когда будет завершен перебор всех элементов матрицы A. В рассмотренном алгоритме обработка была организована построчно.

Теперь рассмотрим пример обработки матрицы по столбцам.

ПРИМЕР 10.3. Задана матрица C(MxN). Сформировать вектор D(N), каждый элемент которого равен минимальному элементу соответствующего столбца матрицы. Алгоритм решения приведен на рис. 10.4.

Так как минимальный элемент необходимо найти для каждого столбца, то обработка будет организована по столбцам. Это значит, что j- будет параметром внешнего цикла, а i –параметром внутреннего. На этот раз организован перебор каждого столбца. Каждый столбец представляет собой одномерный массив. А метод поиска минимального элемента одномерного массива был разобран ранее. В ячейку min помещалось значение 1 –го элемента массива и начиная со 2-го все элементы сравнивались с min. Если сравниваемый элемент оказывался меньше, то в min помещалось его значение.

Первый элемент каждого столбца расположен в 1-ой строке матрицы. Каждый раз перед перебором элементов очередного столбца его первый элемент помещается в min. А сравнение начинается со 2-го элемента столбца. Далее все происходит как и в случае с одномерным массивом, за исключением того, что поиск минимального элемента повторяется N раз – по количеству столбцов в матрице.

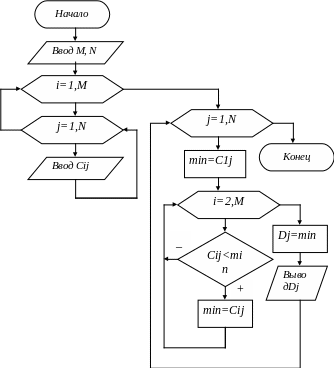
Рис. 10.4. Алгоритм решения примера 10.3.