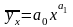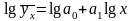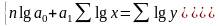Изучение статистической взаимосвязи социально-экономических явлений.

1.Понятие характеристика статистической связи.

2. Формально-статистические методы анализа.

3.Корреляционно-регрессионный метод анализа:

а) парная корреляция;

б) множественная корреляция.

4. Показатели тесноты связи:

а) параметрические;

б) непараметрические.

1. Понятие и характеристика статистической взаимосвязи.

Изучение взаимосвязей – важнейшая задача статистики. В ее основе - изучение социально-экономической сущности явлений.

Статистические методы изучения взаимосвязи позволяют:

1. выявить наличие и направление связи между признаками;

2. измерить эту связь количественно;

3. выразить связь аналитически (с помощью математической функции).

Связи между явлениями и признаками принято характеризовать по ряду направлений:

1. по роли признаков во взаимосвязи:

а) факторные б) результативные

2. по характеру зависимости явлений различают:

а) функциональную, т.е. полную;

б) корреляционную (неполную) или статистическую связь.

3. по направлению различают прямые и обратные связи.

4. по степени тесноты связи различают сильные (тесные), средние и слабые взаимосвязи.

5. по числу взаимодействующих признаков различают:

а) парную связь (парную корреляцию), т.е. связь двух признаков;

б) множественную связь (множественную корреляцию), т.е. связь нескольких признаков.

6. по аналитическому выражению различают линейные (прямолинейные) и нелинейные (криволинейные) связи.

7. по опосредованности связи различают:

а) непосредственные связи;

б) опосредованные (косвенные) связи.

2. Формально статистические методы изучения взаимосвязи.

Для выявления связи, ее характера и направления пользуются формально статистическими методами анализа. К ним относятся: метод параллельных рядов, балансовый метод, метод аналитических группировок, графический метод.

Графический метод предполагает изображение на плоскости множества пар наблюдений, т.е. X и Y. В результате чего получают поле корреляции, позволяющее по концентрации точек сделать предположение и возможной форме взаимосвязи между факторным и результативным признаком и ее направлением.

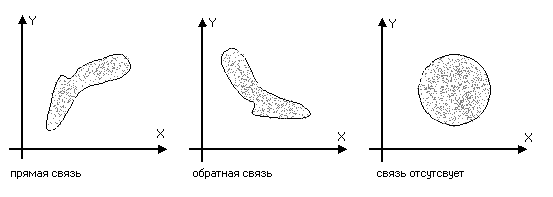
Если точки беспорядочно расположены на плоскости, то связь между признаками отсутствует.

Графический метод позволяет построить эмпирическую линию регрессии по данным наблюдения.

Для этого определяют средние значения Y и серединное значение Х и эти пары точек наносят на плоскость. Соединив точки, получают ломаную эмпирическую линию регрессии. На основе эмпирической линии регрессии можно определить предполагаемую форму взаимосвязи между признаками.

3. Корреляционно-регрессионный метод изучения взаимосвязи:

а) парная корреляция;

б) множественная корреляция.

Парная корреляция.

Корреляционно-регрессионный метод анализа позволяет решить 2 задачи:

1)определить аналитическую форму связи между факторным и результативным признаками (между X и Y);

2) установить меру тесноты связи между признаками, т.е. в какой мере вариация факторного признака (X) обуславливает вариацию результативного признака (Y).

y=f(x)

Корреляционно-регрессионный метод анализа включает в себя несколько этапов:

1. постановка задачи и выбор факторных и результативных признаков;

2. изучение взаимосвязей с помощью формально-статистических методов анализа;

3. выбор формы взаимосвязи между факторным и результативным признаком;

4. измерение тесноты взаимосвязи между факторным и результативным признаком;

5. оценка результатов исследования, пояснения и анализ.

Парная корреляция:

1. линейная корреляция имеет место при равномерном изменении признаков.

,

где 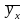- выровненные или теоретические значения признака,

a₀, a₁ – параметры уравнения.

Сущность метода наименьших квадратов состоит в том, что отыскиваются такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических (эмпирических) значений результативного признака от теоретических (вычисленных по функции выравнивания) будет минимальной.

Для нахождения минимума функции приравниваются к нулю частные производные по а₀ и по а_1.

В результате этого получают систему нормальных уравнений:

,

где n – число наблюдений (количество пар X и Y)

Решая систему уравнений, находят параметры а₀ и а₁.

2. Если в качестве уравнения связи выбрана парабола второго порядка

3. Если установлено наличие обратной связи между признаками, то функцией связи может являться гипербола

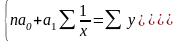
4. Уравнение связи может быть выражено степенной функций: