12. Нелинейное программирование(нп). Трудности, порожденные нелинейностью. Графический метод решения задач нелинейного программирования.

Как известно, общая задача математического программирования формулируется следующим образом: найти вектор X = (x₁, . . . , x_n), удовлетворяющий системе ограничений

g_i (x_{1, . . . ,} x_n) = b_i i = 1 . . . k

g_i (x_{1, . . . ,} x_n) ≤ b_i i = k + 1, . . . , m

и доставляющий экстремум функции Z = f (x_{1, . . . ,} x_n).

При этом предполагается, что известны функции g_i (x_{1, . . . ,} x_n) и f (x_{1, . . . ,} x_n). Обычно на некоторые переменные x_{1, . . . ,} x_n накладывается условие неотрицательности. Кроме того, ограничением может служить условие целочисленности решения для ряда переменных. Если

n

1. g_i (x_{1, . . . ,} x_n) = ∑ a_ijx_j i=1..m,

i=1

n

2. Z = f (x_{1, . . . ,} x_n) = ∑ C_jx_j,

j=1

где a_ij и C_j - известные константы, то при условии неотрицательности решения получаем задачу ЛП. Любую другую задачу математического программирования, не удовлетворяющую условиям (1) и (2), условимся считать нелинейной.

Класс задач нелинейного программирования шире класса задач ЛП. Подробное изучение практических задач, которые условились считать линейными, показывает, что они в действительности являются нелинейными. Возникает задача нахождения эффективных методов решения задач нелинейного программирования. Существующие методы позволяют решать узкий класс задач, ограничения которых имеют вид (1). Даже если область допустимых решений выпуклая, то в ряде задач целевая функция может иметь несколько локальных экстремумов. С помощью большинства же вычислительных методов можно найти точку локального оптимума, но нельзя установить, является она точкой глобального (абсолютного) оптимума или нет. Если в задачах ЛП точка экстремума является вершиной многогранника решений, то в задачах нелинейного программирования она может лежать в вершине многогранника, на ребре или внутренней области. Если задача содержит нелинейные ограничения, то область допустимых решений не является выпуклой и кроме глобального оптимума могут существовать точки локального оптимума.

Также как и в ЛП задачи нелинейного программирования могут быть решены графически.

Пример.Н айти минимальное и максимальное значения сепарабельной функции Z = (x₁ - 4)² + (x₂ - 6)² при ограничениях:

x₁ + x₂ ≥1

2x₁ + 3x₂≤ 12

x₁≥0, x₂≥0.

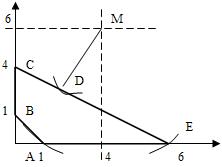
Решение. Область допустимых решений представляет собой многоугольник ABCE. Если положить Z = Q (Q>0), то получим уравнение окружности (x₁ –4) + (x₂ - 6) = Q. С уменьшением (увеличением) Q (квадрата радиуса) значения функции Z соответственно уменьшаются (увеличиваются). Проводя из точки М, как из центра, окружности различных радиусов, получим: минимальное значе ние функция

Z(D) = 196/13 принимает в точке D (24/13; 36/13), в которой окружность касается области решений. Точка D не является угловой, ее координаты находят в результате решения системы уравнений, соответствующих прямым MD и CE. Функция Z имеет два локальных максимума: в вершине А(1;0) функция Z(A) = 45, в вершине E(6;0) функция Z(E) = 5, в вершине C(0;4) функция Z(C) = 25, причем глобальный максимум достигается в вершине С.