10. Целочисленное программирование. Особенности задач, не позволяющие использовать методы лп.

Значительная часть экономических задач, относящихся к задачам ЛП, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например, распределение производственных заданий между предприятиями, раскрой материалов, загрузка оборудования, распределение судов по линиям, самолетов по рейсам, а также задачи по производству неделимой продукции. Если единица составляет малую часть всего объема производства, то оптимальное решение находят обычным симплексным методом, округляя его до целых единиц, исходя из смысла задачи. В противном случае округление может привести к решению, далекому от оптимального целочисленного решения.

Задача целочисленного программирования (не позволяющая использовать методы ЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должно быть целыми неотрицательными числами.

n

Найти минимальное значение линейной функции Z = ∑ a_ijx_j = b_i i = 1..m, j = 1..n, x_j – целые.

x_j ≥ 0. J=1

Предположим, что задача ЛП имеет многогранник решений, рис.1. 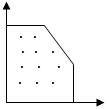Если наложить требование целочисленности, то допустимое множество решений выродится в систему точек и уже не является выпуклым. Если добавить новые ограничения, связывающие внешние целочисленные точки, а затем в качестве многогранника решений использовать все выпуклое множество, ограниченное осями координат и новым контуром, то получим новую задачу ЛП со следующими свойствами:

• новый многогранник решений содержит все целые точки, заключавшиеся в первоначальном многограннике решений; любая его угловая точка является целой;

• так как линейная функция достигает оптимума в угловой точке многогранника решений, то построением такого многогранника и обеспечивается целочисленность оптимального решения.

Метод решения поставленной задачи – метод Гомори, который основан на симплексном методе. Симплексным методом находится оптимальный план задачи без учета целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают. Если же оптимальный план содержит хотя бы одну дробную компоненту x_i, то накладывают дополнительное ограничение, учитывающее целочисленность .

Г 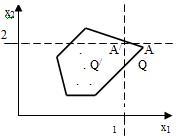еометрический смысл дополнительного ограничения: пусть в точке А многогранника решений Q функция Z достигает максимального значения Z(A) = max, но координаты точки А – дробные. Тогда введеные ограничения по целочисленности 1 и 2 от области Q отсекают область Q^/ с угловой точкой A^/ , координаты которой целочисленные и в которой линейная функция достигает максимального значения.

Метод Гомори. (Идея, геометрическая интерпретация, алгоритм)

Задача целочисленного линейного программирования ставится аналогично рассмотренной обычной задаче линейного программиро­вания. Однако, кроме условия неотрицательности переменных, в данном случае налагается дополнительное условие целочисленности.

Решение таких задач сводится к решению ряда специально по­строенных задач, каждая из которых получается из исходной путем добавления к ее условиям дополнительного линейного ограничения (сечения). При этом k - м сечением будет линейное ограничение, вво­димое в задачу для образования расширенной задачи и удовлетво­ряющее условиям:

• любое целочисленное решение исходной зада­чи ему удовлетворяет;

• любое нецелочисленное решение исходной задачи ему не удовлетворяет.

При решении задач целочисленного программирования по ме­тоду Гомори первый этап не отличается от обычного расчета по симплекс-методу, т.е. на первом этапе целочисленность игнориру­ется до получения оптимального плана.

Пусть задача линейного программирования решена симплекс-методом и ее оптимальное решение не удовлетворяет условиям целочисленности. Тогда составляется дополнительное ограничение. Дополнительное ограничение записывается в виде

где дробные части чисел (a_ij) и (b_i).

Решение задач целочисленного программирования выполняется в следующем порядке:

• решается исходная задача до получения оптимального решения;

• если оптимальное решение целочисленно, то процесс заканчивается, если условия целочисленности не выполняются, то переходят к следующему пункту;

• на основании последней симплекс-таблицы оптимального плана для базисной пе­ременной, имеющей наибольшую дробную часть, строится сечение;

• добавление сечения (ограничения) к условиям оптимального не­целочисленного плана приводит к образованию расширенной зада­чи, после чего возвращаются к п. 1.

Рассмотрим пример: найти хотя бы одно оптимальное целочисленное решение задачи

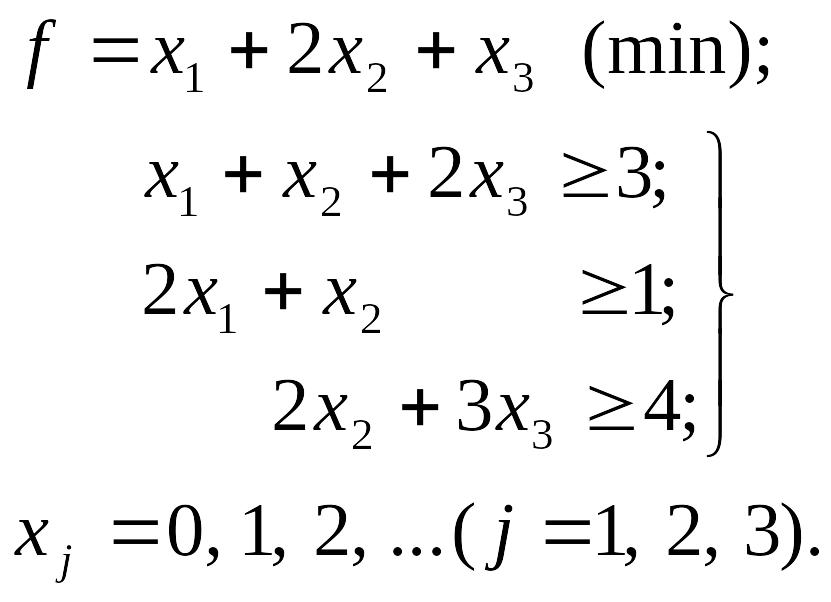
Для решения можно использовать двойственный симплекс-метод.Условия задачи представлены в виде таблицы модифицирован­ных жордановых исключений (табл. 4.1).

БП	1	-x1	-x2	-x3
x4	-3	-1	-1	-2
x5	-1	-2	-1	0
x6	-4	0	-2	-3
F	0	-1	-2	-1

Выбираем разрешающий. В столбце свободных членов выбираем максимальный по модулю отрицательный элемент (т.к. в F-стоке нет положительных элементов). Эта строка становится разрешающей. Составляем симплекс-отношение: т.е. элементы F-строки делим на элементы разрешающей строки, если они одного знака. Выбираем минимальное – этот столбец становится разрешающим.

БП	1	-x1	-x2	-x6
x4	-1/3	-1	1/3	-2/3
x5	-1	-2	-1	0
X3	4/3	0	2/3	-1/3
F	4/3	-1	-4/3	-1/3

Составляем новую симплекс-таблицу: На место разрешающего элемента ставим обратный элемент, повторяем все действия аналогично.

БП	1	-x5	-x2	-x6
x4	1/6	-1/2	5/6	-2/3
x2	1/2	-1/2	1/2	0
X3	4/3	0	2/3	-1/3
F	11/6	-1/2	-5/6	-1/3

В f - строке условие критерия выполняется. Однако полученный план недопустимый. В столбце свободных членов все элементы от­рицательны. Проделав две операции симплексных преобразований, получим оптимальное, по нецелочисленное решение/

Значение целевой функции для плана x*₁ = (1/2; 0; 4/3; 1/6; 0; 0) равно f₁min = 11/6.

Строим дополнительное ограничение. Наибольшую дробную часть имеет базисная переменная

Вводим дополнительное ограничение. Тогда таблица примет следующий вид.

БП	1	СП
		-x5 -x2 -x6
x4= x1= x3= x7=	1/6 1/2 4/3 -1/2	-1/2 5/6 -2/3 -1/2 1/2 0 0 2/3 -1/3 -1/2 -1/2 0
f=	0	-1/2 -5/6 -1/3

БП	1	СП
		-x7 -x2 -x6
x4= x1= x3= x5= x8=	-2/3 1 4/3 1 -2/3	-1 4/4 -2/3 -1 1 0 0 2/3 -1/3 - 2 1 0 0 -1/3 -1/3
f=	7/3	-1 -1/3 -1/3

Используя двойственный симплекс-метод, получим на следующем шаге оптимальное, но нецелочисленное решение.

К базисной переменной x₄, имеющей наибольшую дробную часть, составим дополнительное ограничение. С этой целью в табл. 4.4 предварительно оставляем место для новой базисной дополнитель­ной переменной x₈. Для этого необходимо от свободного члена и коэффициентов при свободных базисных переменных x₇, х₂ и х₆ взять дробную часть и записать ее в соответствующем столбце с противоположным знаком.

Проделав симплексные преобразования с разрешающим элемен­том —1/3, выделенным в табл, получим новый уже полностью целочисленный план. Для оптимального целочисленного плана х* = (1; 0; 2; 2; 1; 2; 0; 0) значение целевой функции f_min=3.

БП	1	СП
		-x7 -x2 -x8
x4= x1= x3= x5= x6=	2 1 2 1 2	-1 4/3 -2 -1 1 0 0 2/3 -1 -2 1 0 0 1 -3
f=	3	-1 0 -1

Метод решения поставленной задачи – метод Гомори, который основан на симплексном методе. Симплексным методом находится оптимальный план задачи без учета целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают. Если же оптимальный план содержит хотя бы одну дробную компоненту x_i, то накладывают дополнительное ограничение, учитывающее целочисленность .

Г еометрический смысл дополнительного ограничения: пусть в точке А многогранника решений Q функция Z достигает максимального значения Z(A) = max, но координаты точки А – дробные. Тогда введеные ограничения по целочисленности 1 и 2 от области Q отсекают область Q^/ с угловой точкой A^/ , координаты которой целочисленные и в которой линейная функция достигает максимального значения.