2. Алгоритм двойственного симплекс-метода.

Пусть имеем исходную задачу линейного программирования в канонической форме записи:

Двойственный симплекс-метод, или метод последовательного уточнения оценок, как и симплекс-метод, заключается в последова­тельном переходе от одного n-мерного вектора к другому. Однако в отличие от симплекс-метода эти последовательно получаемые век­торы не обязательно удовлетворяют условию неотрицательности.

Двойственный симплекс-метод - это применение обычного симплекс-метода к двойственной задаче, дополненное построением на каждом шаге n-мерного вектора, являющегося почти допусти­мым опорным решением данной задачи.

Запишем двойственную задачу на основе исходной:

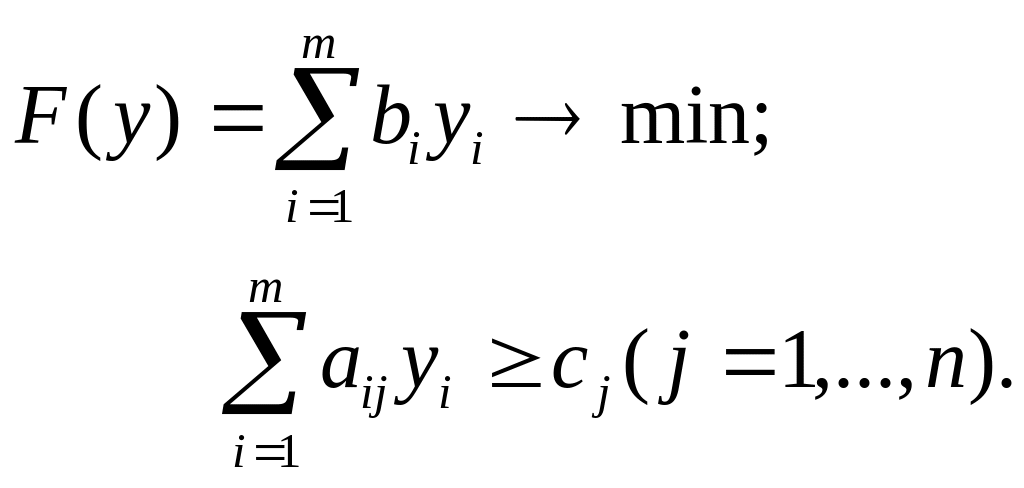
y_i  0 (i = 1,…,m)

Алгоритм ее построения следующий:

• в F-й строке находится положительное число, которому со­ответствует разрешающий столбец;

• в выделенном столбце отыскивается положительное число и содержащая его строка берется разрешающей; если в выделенном столбце нет положительных чисел, то задача не имеет решения;

• вычисляются двойственные модифицированные отношения элементов F-й строки соответственно к элементам разрешающей строки; отношение с наименьшей абсолютной величиной указывает разрешающий элемент.

• Первый этап решения заканчивается, если все коэффициенты (за исключением, возможно, свободного элемента) отрицательны. На втором этапе за разрешающую принимается строка с наименьшим отрицательным свободным членом; разрешающий столбец определя­ется так же, как и на первом этапе.

Рассмотрим следующий пример: двойственным симплекс-методом решить задачу, двойственную исходной, и записать решение исходной:

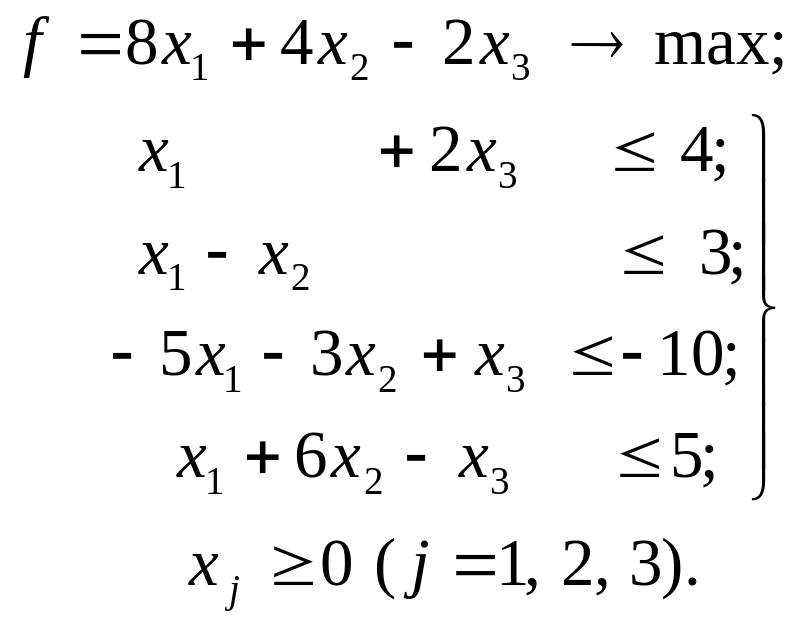
Двойственная задача запишется в виде:

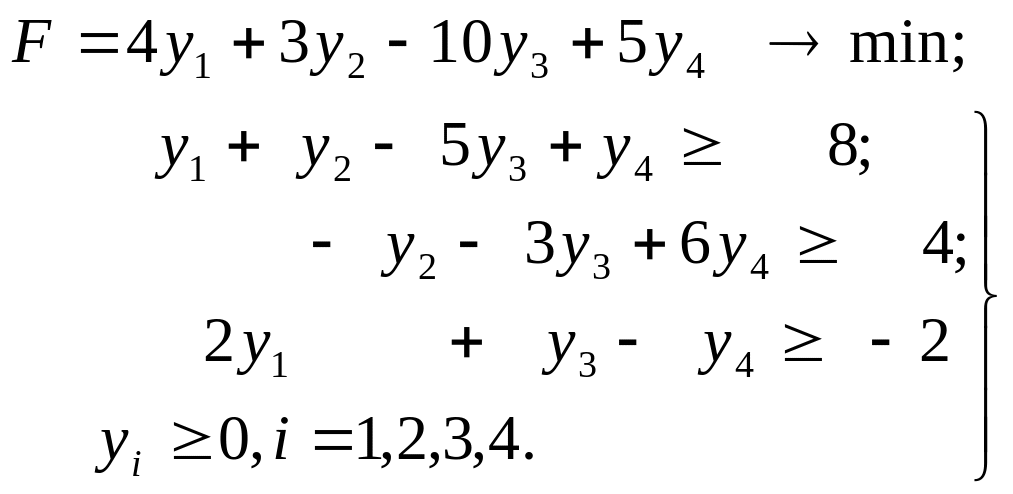
Условия двойственной задачи представим в симплекс-таблице:

БП	1	-y1	-y2	-y3	-y4
y4	-8	-1	-1	5	-1
y5	-4	0	1	3	-6
y6	2	-2	0	-1	1
F	0	-4	-3	10	-5

Поскольку в F- строке имеется положительное число, то третий столбец примем за разрешающий(выделено серым цветом). В данном столбце есть два положительных числа 5 и 3. Возьмем, например, число 5; примем первую строку за разрешающую(выделено серым цветом). Для выбора разрешающего элемента выберем наименьшее двойственное отношение по модулю элементов F- строки соответственно к элементам первой строки, (т.е. элементы F- строки делим на элементы разрешающей строки)

Разрешающий элемент равен 5.

На место разрешающего элемента ставим обратный элемент (1/5)

Элементы разрешающей строки делим на разрешающий элемент (-8/5; -1/5; -1/5; -1/5). Элемент разрешающего столбца делим на разрешающий элемент с обратным знаком (3/-5 = -3/5; -1/-5 = 1/5; 10/-5 = -2). Остальные элементы вычисляем по формуле:

, где h – разрешающая строка; l – разрешающий столбец.

Т.е. -4 -3 * (-8/5) =4/5; 2- (-1) *(-8/5) = 2/5; 0 – 3 * (-1/5) = 3/5; 0 – 10 * (-8/5) = 16; -2 –(-1) * (-1/5) = -11/5; -4 –10 * (-1/5) = -2; 1- 3 * (-1/5) = 8/5; 0- (-1) * (-1/5) = -1/5; -3 –10 * (-1/5) = -1; -6 –3 * 1/5 = -27/5; 1- (-1) * (-1/5) = 4/5; -5 –10 * (-1/5) = -3.

Свободную и базисную переменную меняем местами (переменная y₃ перейдет в ба­зисную переменную вместо -y₅). В F-строке условие критерия оптимальности выполняется (все элементы отрицательные), однако в столбце свободных членов имеются отрицательные элементы, следовательно, получен­ное решение недопустимо. Составляем следующую симплекс-таблицу:

БП	1	-y1	-y2	-y5	-y4
y3	-8/5	-1/5	-1/5	-1/5	-1/5
y5	4/5	3/5	8/5	-3/5	-27/5
y6	2/5	-11/5	-1/5	1/5	4/5
F	16	-2	-1	-2	-3

Первую строку принимаем за разрешающую, поскольку в ней свободный элемент отрицательный (-8/5). Определяем разрешаю­щий столбец:

БП	1	-y1	-y3	-y5	-y4
y2	8	1	-5	-1	1
y5	-12	-1	8	1	-7
y6	2	-2	-1	0	1
F	24	-1	-5	-3	-2

Составляем следующую симплекс-таблицу:

В табл. вторая строка разрешающая. Определим наимень­шее двойственное отношение по модулю:

БП	1	-y1	-y3	-y5	-y6
y2	44/7	6/7	-27/7	-6/7	1/7
y5	12/7	1/7	-8/7	-1/7	-1/7
y4	2/7	-15/7	1/7	1/7	1/7
F	192/7	-5/7	-51/7	-23/7	-2/7

Разрешающий столбец четвертый, соответствующий y₄. Проделав шаг симплексных преобразований, получим:

Оптимальное решение двойственной задачи у* = (0; 44/ 7; 0; 12/ 7; 0; 0; 2/ 7); F = 192/ 7. Числа F- строки—значения пере­менных оптимального плана исходной задачи. С учетом соответ­ствия между переменными

y₁  x₄

y₂  x₅

y₃  x₆

y₄  x₇

y₅  x₁

y₆  x₂

y₇  x₃

можно записать решение исходной за­дачи, взяв элементы F-строки с противоположным знаком:

х* = (23/7; 2/7; 0; 5/7; 0; 5/7; 0). В соответствии с теоремой 1(билет 7) значение целевой функции исходной задачи

f = 192/ 7.

Пример2 (этот пример был в тетрадке, он решен обычным симплекс-методом, т.к. в F-строке нет положительных элементов): Построить двойственную задачу, решить одну из них и записать решение другой задачи, если исходная задача име­ет вид

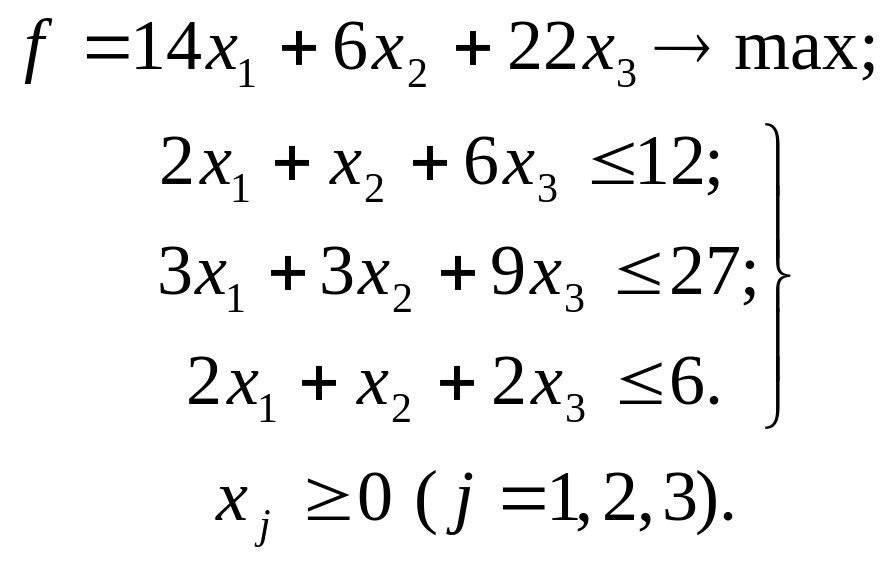
Решение. Двойственная задача запишется в виде

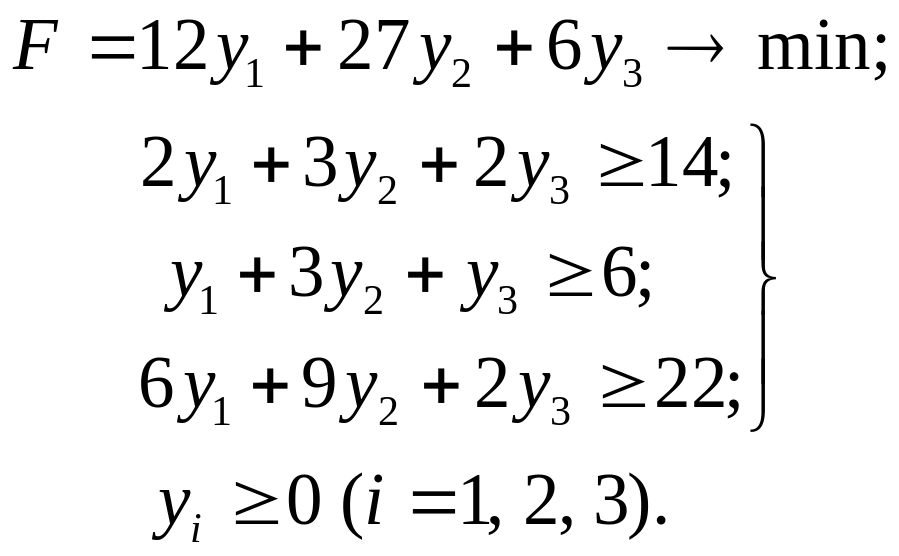
Составляем симплекс-таблицу:

БП	1	-y1	-y2	-y3
y4	-14	-2	-3	-2
y5	-6	-1	-3	-1
y6	-22	-6	-9	-2
F	0	-12	-27	-6

Составляем модифицированные симплекс-отношения. Для этого элементы F – строки делим на элементы разрешающей строки. Выбираем минимальное. Первый шаг продолжаем до тех пор, пока в F – строке все элементы не станут отрицательными.

Замечание: Если в F – строке есть положительный элемент, а в соответствующей строке нет положительных элементов, то система несовместна.

Рассматриваем столбец свободных членов. Находим мах по модулю отрицательный элемент. Эта строка разрешающая(она выделена серым цветом). Элементы F – строки делим на элементы разрешающей строки, если они одного знака:

(-12/-6=2, -27/-9=3, -6/-2=3).

Среди этих элементов выбираем min:(он равен 2(-12/-6=2)). Столбец, в котором находится этот min элемент является разрешающим (он выделен серым цветом). Разрешающий элемент находится на пересечении разрешающей строки и разрешающего столбца.

БП	1	-y1	-y2	-y3
y4	-14	-2	-3	-2
y5	-6	-1	-3	-1
y6	-22	-6	-9	-2
F	0	-12	-27	-6

Строим новую симплекс – таблицу, причем свободную переменную и базисную меняем местами. На место разрешающего элемента ставим обратный элемент (т.е. –6 меняем на -1/6). Элемент разрешающей строки делим на разрешающий элемент (т.е. –22 делим на –6 получаем –22/-6 = 11/3; -9/-6 = 3/2; -2/-6 = 1/3), а элемент разрешающего столбца делим на разрешающий элемент с обратным знаком (-2/6 = -1/3; -1/6; -12/6 = -2). Остальные элементы вычисляем по формуле:

, где h – разрешающая строка; l –разрешающий столбец.

!!! Т.е. –14 - (-2) * -22/-6 = -14 + 22/3 = -20/3; -6 –(-1) * -22/6 = -6 + 22/6 = -7/3; 0 – (-12) * -22/6 = 44; -3 – (-2) * -9/-6 = 0;

-3 – (-1) * -9/-6 = -3/2; -27 – (-12) * -9/-6 = -9; -2 – (-2) * -2/-6 = -4/3; -1 – (-1) * -2/-6 = -2/3; -6 – (-12) * -2/-6 = -2.

БП	1	-y6	-y2	-y3
y4	-20/3	-1/3	0	-4/3
y5	-7/3	-1/6	-3/2	-2/3
y1	11/3	-1/6	3/2	1/3
F	44	-2	-9	-2

Составляем новую симплекс таблицу. Выбираем разрешающий элемент, для этого снова рассматриваем столбец свободных членов и выбираем по модулю отрицательный элемент – эта строка становится разрешающей (выделена серым цветом). Элементы F-строки делим на элементы разрешающей строки, если они одного знака

(т.е. –2/(-1/3) = 6; -2/(-4/3 = 3/2)). Среди этих элементов выбираем min отношение. Столбец, в котором находится это min отношение становится разрешающим (выделено серым цветом). На место разрешающего элемента ставим обратный элемент (-3/4). Свободную переменную и базисную меняем местами. Элемент разрешающей строки делим на разрешающий элемент (т.е. –20/3 делим на –4/3 получаем 5; -1/3 : -4/3 = 1/4; 0 : -4/3 = 0), а элемент разрешающего столбца делим на разрешающий элемент с обратным знаком (-2/3 : 4/3 = -1/2; 1/3 : 4/3 = 1/4; -2 : 4/3 = -3/2). Остальные элементы вычисляем по той же формуле.

БП	1	-y6	-y2	-y4
y3	5	1/4	0	-3/4
y5	1	0	-3/2	-1/2
y1	2	-1/4	3/2	1/4
F	54	-3/2	-9	-3/2

Получили оптимальный план (т.к. все элементы в столбце свободных членов стали положительными).

Ответ: У^* = (2; 0; 5; 0; 1; 0); F = 54.

Установим соответствие между переменными пары двойствен­ных задач. Приводя задачи к канонической форме, будем иметь системы ограничений исходной и двойственной задач, содержащие одинаковое число переменных. В нашем случае таких переменных будет шесть. Дополнительные переменные x₄, x₅, x₆ исходной задачи соответствуют свободным переменным двойственной задачи, т. е.

y₁  x₄

y₂  x₅

y₃  x₆

Аналогично дополнительные пе­ременные y₄, y₅, y₆ двойственной задачи соответствуют свободным переменным исходной задачи, т. е.

y₄  x₁

y₅  x₂

y₆  x₃

C учетом соответствия между переменными и теоре­мы 1(билет 7) решение двойственной задачи записываем так:

X^* = (3/2; 0; 3/2; 0; 9; 0). Опти­мальное значение целевой функции равно f = 54.