
- •Формы записи задачи линейного программирования (лп) (произвольная, симметричная, каноническая). Переходы от одной формы записи к другой.
- •Свойства решений задачи л.П. (основные теоремы и следствия).
- •Графический метод. Решения задачи лп.
- •Симплекс-метод (идея, условие оптимальности). Алгоритм симплекс-метода.
- •Метод искусственного базиса или м-задача (область применения метода, идея и алгоритм)
- •Двойственные задачи линейного программирования (Правила построения двойственных задач, теоремы двойственности).
- •Алгоритм двойственного симплекс-метода.
- •Целочисленное программирование. Особенности задач, не позволяющие использовать методы лп.
- •Транспортная задача. Метод потенциалов.
- •Транспортная задача на сети.
- •Нелинейное программирование(нп). Трудности, порожденные нелинейностью. Графический метод решения задач нелинейного программирования.
- •Классические методы оптимизации. Метод множителей Лагранжа.
- •Динамическое программирование. Метод функционального программирования. Задача распределения ресурсов.
- •Теория игр. Цена игры. Седловая точка игры.
- •Теория игр. Игра в смешанных стратегиях.
Метод искусственного базиса или м-задача (область применения метода, идея и алгоритм)
Если задача сформулирована в канонической форме
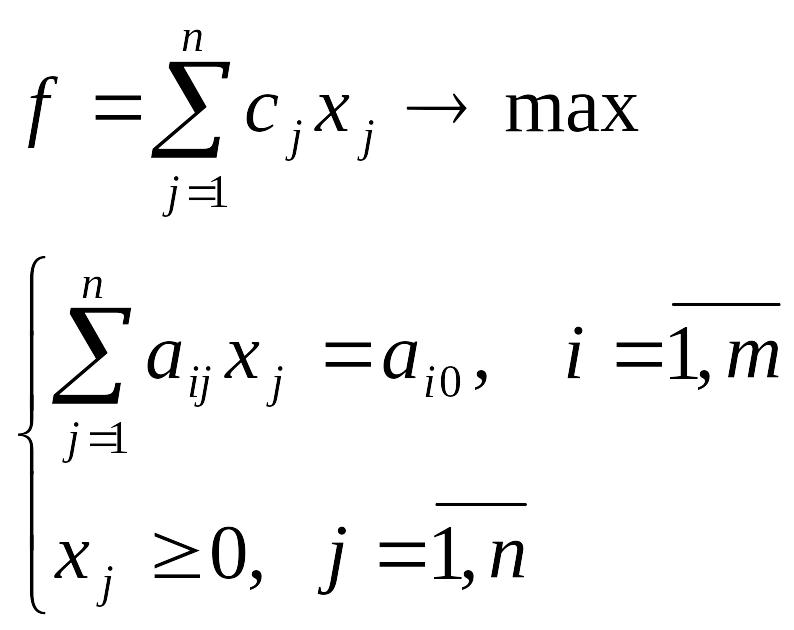

и базис выделить нельзя без каких-либо дополнительных действий, то можно составить М-задачу в следующем виде:
где xn+i – искусственная базисная переменная. Далее составляется расширенная симплекс-таблица. Цель: исключить искусственные переменные из симплекс-таблицы.
Рассмотрим алгоритм на примере:
![]()

Составим М-задачу: F=x1+2x2-x3+x4-M(x5+x6)→ max
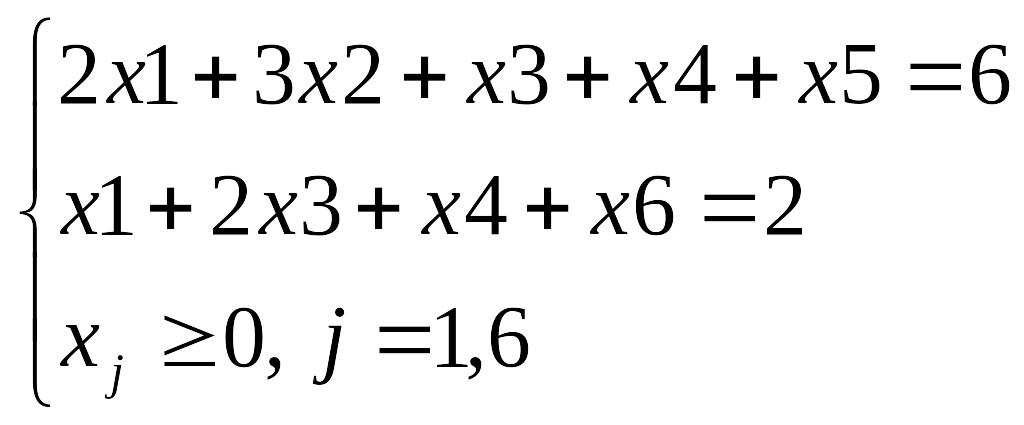
Составляем расширенную симплекс-таблицу:
БП |
1 |
-х1 |
-х2 |
-х3 |
-х4 |
х5 |
6 |
2 |
3 |
1 |
1 |
х6 |
2 |
1 |
0 |
2 |
1 |
f |
0 |
-1 |
-2 |
1 |
-1 |
M |
-8 |
-3 |
-3 |
-3 |
-2 |
БП |
1 |
- |
-х2 |
-х3 |
-х4 |
х5 |
2 |
-2 |
3 |
-3 |
-1 |
х1 |
2 |
1 |
0 |
2 |
1 |
f |
2 |
1 |
-2 |
3 |
0 |
М |
-2 |
3 |
-3 |
3 |
1 |
БП |
1 |
-х3 |
-х4 |
х2 |
2/3 |
-1 |
-1/3 |
х1 |
2 |
2 |
1 |
f |
10/3 |
1 |
-2/3 |
М |
0 |
0 |
0 |
Если в М-строке все нули и все искусственные переменные исключены из базиса, то М-строка выбрасывается и далее следует обычный симплекс-метод.
Если в М-строке существуют элементы >0 и все искусственные переменные исключены из базиса, то система несовместна.
Если в М-строке существуют элементы >0 и не все искусственные переменные исключены из базиса, то разрешающий элемент выбирается таким образом, чтобы исключить искусственную переменную из базиса.
БП |
1 |
-х3 |
-х1 |
х2 |
4/3 |
-1/3 |
1/3 |
х4 |
2 |
2 |
1 |
f |
14/3 |
7/3 |
2/3 |
Х*=(0, 4/3, 0, 2)
F(Х*)=14/3
Двойственные задачи линейного программирования (Правила построения двойственных задач, теоремы двойственности).
Теорема1: Если одна из задач двойственной пары имеет решение, то другая задача т.ж. имеет решение. При этом для любых оптимальных планов (Х* = (х1*,…, хn*) – план исходной задачи и У* = (у1*,…, уm*) – план двойственной задачи) имеет место равенство:
f(X*) = F(Y*).
Следствие1: Для разрешимости одной из задач двойственной пары необходимо и достаточно чтобы одна из задач имела хотя бы одно решение.
Следствие2: Если целевая функция одной из задач двойственной пары неограничена, то другая не имеет решение.
Следствие3:Для оптимальности планов Х*, У* пары двойственных задач необходимо и достаточно, чтобы выполнялось равенство.
Теорема2: Для оптимальности допустимых планов Х*, У* пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
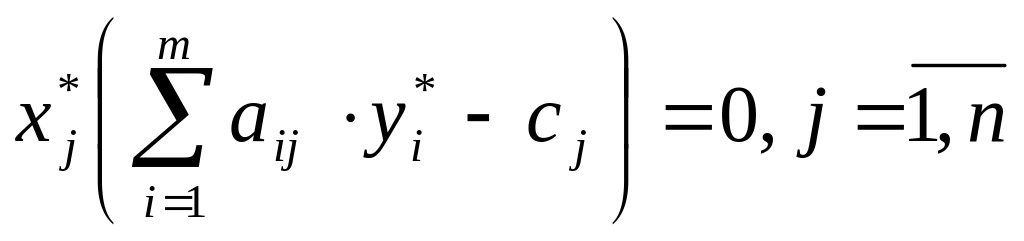

Исходная задача: Двойственная задача
![]()
![]()
AX B ATY 0
X 0 Y 0
Составление двойственной задачи:
Исходная задача |
Двойственная задача |
|
|
Для построения двойственной задачи необходимо соблюдать следующие правила:
каждому i-му ограничению задачи (1) соответствует переменная yi задачи (2), и, наоборот, каждому j-му ограничению двойственной задачи (2) соответствует переменная хj, задачи (1);
матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием, т. е. заменой строк столбцами, с сохранением их порядка;
свободные члены ограничений задачи (1) являются коэффициентами при соответствующих переменных целевой функции двойственной задачи (2); аналогично коэффициенты целевой функции исходной задачи (1) совпадают со свободными членами системы ограничений двойственной задачи (2);
если целевая функция исходной задачи (1) максимизируется, то целевая функция двойственной задачи (2) минимизируется;
в задаче (1) ограничения-неравенства следует записывать со знаком ≤, а для задачи (2) — со знаком ≥;
если на j-ю переменную задачи (1) наложено условие неотрицательности, то j-е ограничение задачи (2) будет неравенством, в противном случае j-е ограничение будет равенством; аналогично связаны между собой ограничения задачи (1) и переменные задачи (2).
Построить двойственную задачу к задаче
f
= 3x1
+ 4x2
– x3
+2x4
-5x5
![]() max;
max;
![]()
Чтобы построить задачу, двойственную к данной, упорядочим исходную задачу. Так как требуется найти максимум целевой функции, то ограничения-неравенства должны быть записаны со знаком ≤. Умножив третье неравенство на (-1), приведем систему ограничений к виду (1):
![]()
Двойственная задача будет иметь четыре переменные y1, y2, y3 , y4, так как исходная задача содержит четыре ограничения. В соответствии с указанными правилами запишем двойственную задачу:
F = 12y1 -10y2 +15y3 +11y4 min;
![]()
Второе и пятое ограничения двойственной задачи записаны в виде равенства, так как на соответствующие им переменные x2 и x5 в исходной задаче не наложено условие неотрицательности. На переменные y1, y2, y3 наложено условие неотрицательности в связи с тем, что в исходной задаче, приведенной к виду (1), им соответствуют ограничения-неравенства.


 х6
х6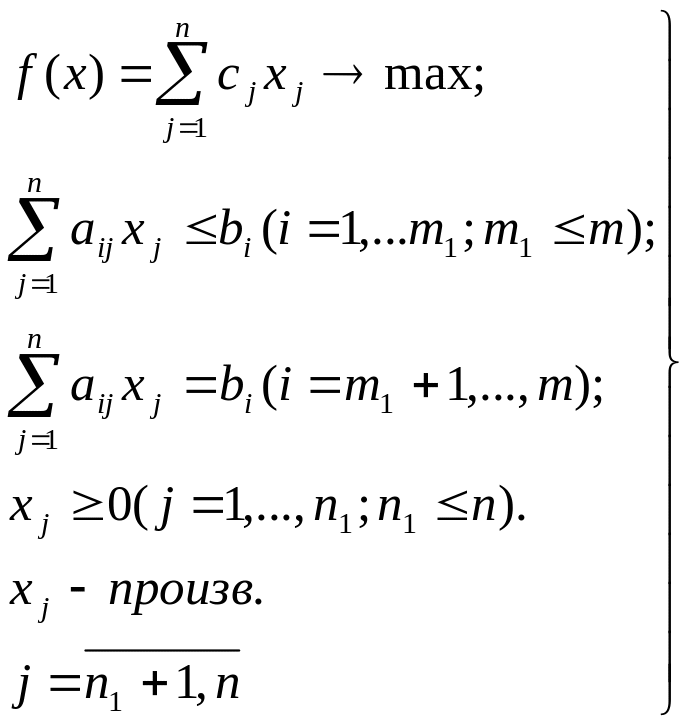 (1)
(1)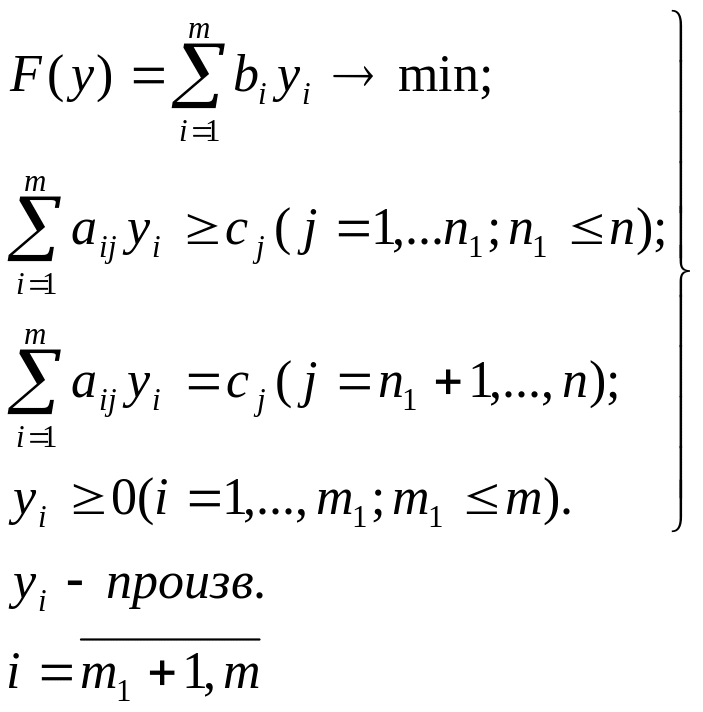 (2)
(2)