Дисциплина «Методы оптимизаций и исследование операций»

2. Общая задача линейного программирования. Понятие допустимого, опорного и оптимального планов. Матричный и векторный способ записи задачи.

Линейное программирование (ЛП) – наука о методах исследования и отыскания наиболее или наименее значение линейной функции, на неизвестной которой наложены линейные ограничения. Приведем формы записи задачи линейного программирования:

• Векторная форма записи.

F = C*X^Т  мах

A₁*x₁ + A₂*x₂ + …+ A_n*x_n =B

X  0

C – вектор – строка = (С₁, С₂ , …, С_n)

X – вектор – столбец = (x₁, x₂, x₃, …, x_n)^Т

В = (b₁, b₂, …, b_n)^Т

A_n =

• Матричная форма записи

F = C*X  мах

AX = B

X  0

A =  а_{i j} , i = 1…m; j = 1…n

• Запись с помощью суммирования.

Планом или допустимым решением задачи ЛП называется вектор X, удовлетворяющий условиям:

• 

• 

• 

• 

• 

План X называется опорным, если векторы А_i, i =1…n, входящие в (A₁*x₁ + A₂*x₂ + …+ A_n*x_n =B) с положительными коэффициентами, являются линейно независимыми. Количество положительных компонент должно быть меньше или равно m, а нулевых - больше n-m.

Опорный план называется невырожденным, если он содержит m положительных компонент.

Оптимальным планом или оптимальным решением называется план, доставляющий наибольшее (наименьшее) значение целевой функции.

2. Формы записи задачи линейного программирования (лп) (произвольная, симметричная, каноническая). Переходы от одной формы записи к другой.

Линейное программирование – наука о методах исследования и отыскания наиболее или наименее значение линейной функции, на неизвестной которой наложены линейные ограничения.

Формы записи задачи линейного программирования:

• произвольная форма записи.

- целевая функция:

Целевая функция должна удовлетворять следующим условиям:

• симметричная форма записи

Целевая функция должна удовлетворять следующим условиям:

• m1 = m;

• n1 = n

• каноническая форма записи

Целевая функция должна удовлетворять следующим условиям:

• m2 = 0;

• n1 = n

• Для того, чтобы поменять знак неравенства, надо домножить на (-1)

• f-min  * (-1)  f-mах

Переход от одной формы записи к другой.

• меняем знак неравенства путем доиножения на (-1)

• f -> min  f*(-1)  f -> mах

• если в задаче не наложено условие х_j≥0, а его надо получить, то вводят 2 переменные

• как от неравенства перейти к равенству: введем дополнительную переменную (балансовую) Х3  0 и добавим ее к левой части неравенства Х1 + Х2  3: Х1 + Х2 + Х3 = 3

• приведение к канонической форме:

F= 3Х1 - 2Х2 - Х3  min

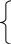2Х1 - Х2 + Х3 2

3Х1 + 2Х2 + Х3  6

Х1 + Х2 + Х3 = 4

Х1  0; Х2  0

Введем F’ = - F = -3Х1 + 2Х2 + Х3  mах

Х 4  0; Х5  0

2Х1 - Х2 + 3Х3 - Х4 = 2

3Х1 + 2Х2 + Х3 + Х5 = 6

Х1 + Х2 + Х3 = 4

Х1  0; Х2  0

F’ = -3Х1 + 2Х2 + Х3’ - Х3’’ mах

2 Х1 - Х2 + Х3’ - Х3’’- Х4 = 2

3Х1 + 2Х2 + Х3’ - Х3’’ + Х5 = 6

Х1 + Х2+ Х3’ - Х3’’ = 4

Х1  0; Х2  0; Х4  0; Х5  0

Х3’ 0; Х3’’ 0

• приведение к симметричной форме:

F = Х1 + 2Х2 - Х3 + Х4 - 2Х5  mах

Х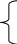 1 - Х2 - 2Х3 = 4

2Х2 + 4Х3 – Х4 = 8

Х2 + Х3 + Х5 = 6

Хj  0, j = 1…5

- Х2 - 2Х3  4

2Х2 + 4Х3  8

Х2 + Х3  6

Х2  0; Х3  0

Подставим в целевую функцию:

Х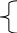 1 = 4 + Х2 +2Х3

Х4 = -8 + 2Х2 + 4Х3

Х5 = -6 - Х2 - Х3

F = (4 + Х2 +2Х3) + 2 Х2 - Х3 – (- 8 + 2Х2 + 4Х3) –2 (6 - Х2 - Х3) = 3Х2 - Х3 mах

-Х2 - 2Х3  4

-2Х2 - 4Х3  -8

Х2 + Х3  6

Х2  0; Х3  0

2. Свойства решений задачи л.П. (основные теоремы и следствия).

Теорема

Множество всех планов задачи линейного программирования выпукло.

Множество выпукло, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию.

Теорема

Целевая функция задачи линейного программирования достигает своего максимального (минимального) значения в угловой точке многогранника решений. Если целевая функция принимает max (min) значение, более, чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Теорема

Если известно, что система векторов А₁, А₂, …А_k (k  n) в разложении:

А₁X₁ + А₂ X₂ +… + А_n X_n = B, Х  0 линейно независима и такова, что А₁X₁ + А₂ X₂ +… + А_k X_k = B, где X_j 0, j = 1,..k, то точка X = (X₁, X₂, … X_k) является угловой точкой многогранника решений.

Теорема

Если Х=(X₁, X₂, … X_n) – угловая точка многогранника решений, то система векторов в разложении А₁X₁ + А₂ X₂ +… + А_n X_n = B, Х  0 является линейно независимой.

Следствие 1.

Т.к. А₁, А₂, …А_m имеют размерность m, то угловая точка многогранника решений имеет не более чем m положительных компонент

X_i >0, i =1,… m

Следствие 2.

Каждой угловой точке многогранных решений соответствует k  m линейно-независимых векторов системы.

В дальнейшем мы всегда будем предполагать что у нас m линейно-независимых векторов.

Иначе систему можно дополнить до m линейно-независимых векторов и решить расширенную задачу.

Замечание.

Если целевая функция задачи линейного программирования ограничена на многограннике решений, то существует такая угловая точка многогранных решений, в которой целевая функция задачи Л.П. достигает своего оптимума.

Каждый опорный план соответствует угловой точке многогранных решений, поэтому достаточно исследовать угловые точки многогранника решений.