3. Производство фирмы в долгосрочном периоде.

В долгосрочный период все факторы производства могут быть переменными. Поэтому один и тот же объем выпуска продукции - Q может быть обеспечен путем использования различных комбинаций переменных факторов. (X^1, X²,...Xⁿ)

Q=f(X¹,X²,...Xⁿ),

Постоянная Переменные

величина величины

Перед каждым производителем в долгосрочный период стоит проблема выбора: как именно произвести ту или иную продукцию? Какие ресурсы использовать в большей или меньшей степени? Ответ на поставленные вопросы зависит не только от характера технологии, но и от стоимости ресурсов, следовательно, проблема выбора решается с позиций технологической и экономической эффективности.

Для точного определения условий эффективного производства данного объема выпуска продукции используем графический метод анализа производственной функции через изокванты( оценивают уровни технологической эффективности выпуска) и изокосты( оценивают область доступных объемов выпуска при данных ценах на ресурсы и объеме финансовых средств, расходуемых фирмой на приобретение ресурсов).

Если отложить (Рис. 2) по горизонтальной оси количество единиц труда(L), по вертикальной - количество единиц капитала(K), затем, обозначить и соединить точки, которые отражают выпуск одного и того же объема продукции при разных комбинациях ресурсов, то получится кривая, представленная на рисунке и называемая изоквантой (IQ1). Набор таких изоквант составляет карту изоквант, отражающую возрастание уровней выпуска продукции.(IQ1, IQ2, IQ3).

Изокванта (isoquant – от слов “iso”- тот же самый и “quant” –количество) - кривая, каждая точка которой показывает альтернативные комбинации ресурсов, которые могут быть использованы для производства определенного объема продукции при данной технологии.

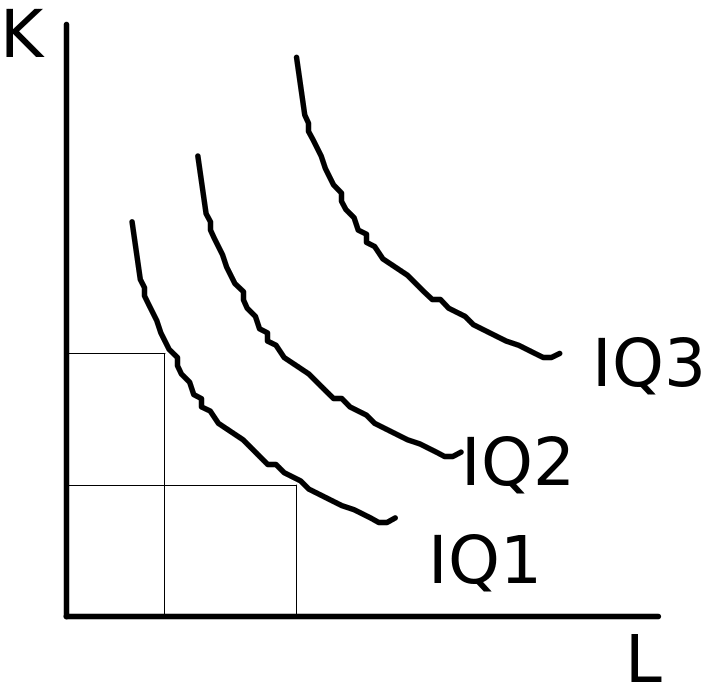
Рис.2. Карта изоквант.

Свойства стандартных изоквант аналогичны характеристикам кривых безразличия.

1). Изокванта, также как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек;

2). Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства.

3). Изокванты, описывающие данную производственную функцию, никогда не пересекаются.

4). Изокванты не имеют участков возрастания.

Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого (К), так и второго (L) ресурса, т.е. возрастал бы объем максимального выпуска, а он(объем) должен быть постоянным на всем протяжении изокванты.

Убывающий характер изокванты отражает возможность замещения в определенных пределах используемых ресурсов, так что совокупный объем выпуска остается неизменным.

Предельная норма технологического замещения (Marginal Rate of Technical Substitution, или MRТS) одного ресурса на другой (например, труда на капитал) показывает степень замещения труда капиталом, при котором объем выпуска остается неизменным.

Алгебраическое выражение, показывающее степень, в которой производитель готов сократить количество капитала в обмен на увеличение труда, достаточную для сохранения прежнего объема выпуска, имеет вид

В силу отрицательного наклона изокванты данное отношение всегда является величиной отрицательной. Иногда для удобства вводят минус перед правой частью, но в большинстве случаев имеет значение абсолютная величина коэффициента.

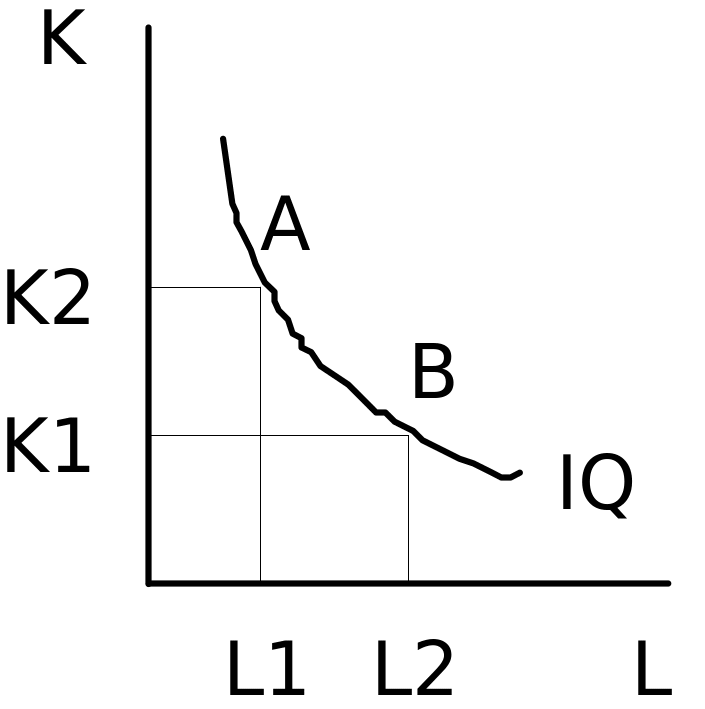
Рис.3. Предельная норма технологического замещения

Как видно на рисунке 3, при переходе из точки А в точку В объем производства остается неизменным. Это означает, что сокращение выпуска в результате уменьшения затрат капитала ( К=К2-К1) компенсируется увеличением выпуска за счет использования дополнительного количества труда ( L=L2-L1).

Cокращение выпуска в результате уменьшения затрат капитала равно произведению К на предельный продукт капитала, или

- К*МРK.

Увеличение выпуска за счет использования дополнительного количества труда в свою очередь равно произведению L на предельный продукт труда, или

L*MPL.

Таким образом, можно записать, что

- К*МРK.= L*MPL.

Запишем данное выражение по иному:

- К/ L=MPL/МРK.

или

Производственная функция, связывающая между собой количество капитала, труда и объем выпуска позволяет также рассчитать предельную норму технологического замещения через производную данной функции:

MRТS= dK/dL

Это значит, что графически в любой точке изокванты предельная степень технологического замещения равна тангенсу угла наклона касательной к изокванте в этой точке.

Очевидно , что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты. При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, т.к. все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала. В дальнейшем MRTS достигает своего предела (MRTS=0), а изокванта приобретает горизонтальный вид ( это изображено на Рис. 4). Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала в точке Е - минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производство данного объема количество труда имеет место в точке А).

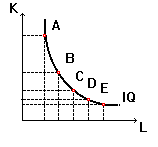
Рис.4. Убывание предельной нормы технологического замещения

Убывание MRTS при замещении одного ресурса другим характерно для большинства производственных процессов и характерно для всех изоквант стандартного вида.

Изокванты нестандартного вида выражают ситуации:

А). Совершенной взаимозаменяемости ресурсов.

Б). Фиксированной структуры использования ресурсов.

А). Если ресурсы, используемые в процессе производства, являются абсолютно заменяемыми, то MRTS постоянна во всех точках изокванты, а карта изоквант имеет вид, как на рисунке 5. Примером может служить производство, допускающее как полную автоматизацию, так и ручное изготовление какого-либо продукта.

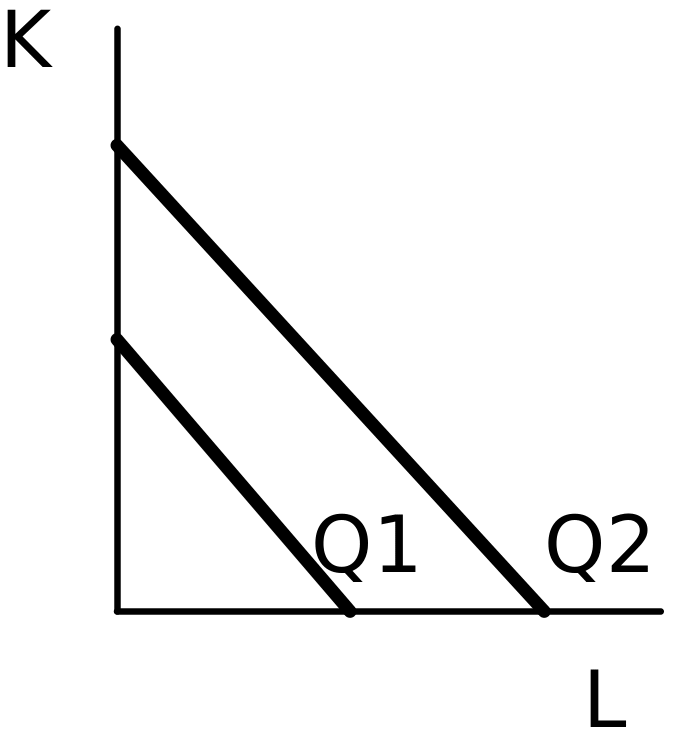
Рис.5 Карта изоквант совершенно взаимозаменяемых ресурсов

Б). Если технологический процесс исключает замещение одного фактора на другой и требует использования обоих ресурсов в строго фиксированных пропорциях, производственная функция (карта изоквант) имеет вид латинской буквы L, как на рисунке 6.

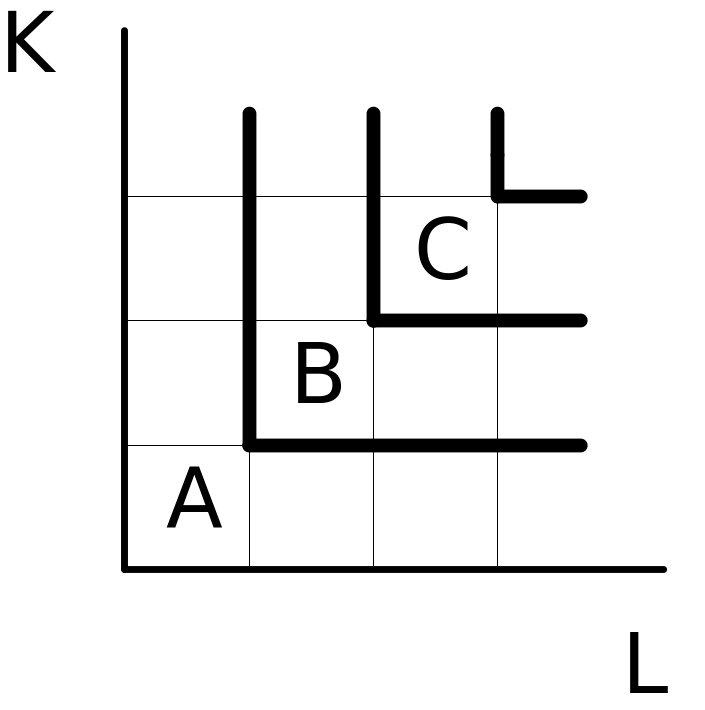
Рис.6. Карта изоквант при фиксированной структуре использования ресурсов

Примером подобного рода может служить работа землекопа (одна лопата и один человек) или обслуживание башенного крана (один крановщик и один кран). Увеличение количества одного из факторов без соответствующего изменения количества другого фактора невозможно, поэтому технически эффективными (оптимальными) будут лишь угловые комбинации ресурсов (точки А, В, С).

Как мы уже выяснили раньше, набор изоквант отдельной фирмы (карта изоквант) показывает технически возможные комбинации ресурсов, обеспечивающие фирме соответствующие объемы выпуска. Однако при выборе оптимальной комбинации ресурсов производитель должен учитывать не только доступную ему технологию, но и свои финансовые ресурсы, а также цены на соответствующие факторы производства.

Совокупность двух последних факторов определяют область доступных производителю экономических ресурсов.

Бюджетное ограничение производителя может быть записано в виде неравенства

,

где Pk, PL - цена капитала и труда,

K, L - количество капитала и труда,

ТС(total cost) - совокупные расходы (издержки) фирмы на приобретение ресурсов.

Если производитель полностью расходует свои средства на приобретение данных ресурсов, то мы получаем равенство

или

.

Полученное уравнение называют уравнением изокосты.

Линия изокосты((isocost – от слов “iso”- тот же самый и “cost” –стоимость), линия неизменных издержек фирмы, представленная на Рис.7, показывает набор комбинаций экономических ресурсов (в данном случае труда и капитала), которые фирма может приобрести с учетом рыночных цен на ресурсы и полном использовании своих финансовых ресурсов.

Наклон линии изокосты определяется отношением рыночных цен на труд и на капитала (-РL/РK), что вытекает из уравнения изокосты.

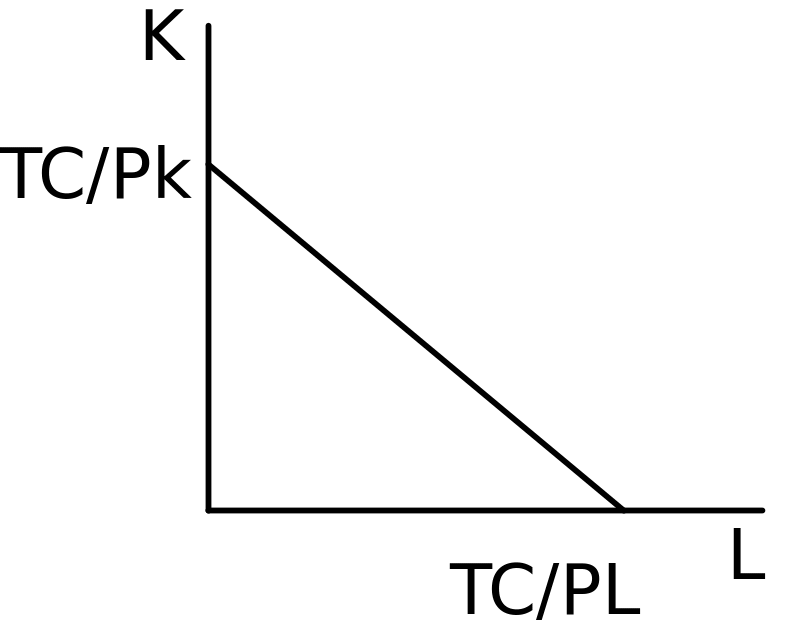
Рис.7 Линия изокосты производителя

Равновесие (оптимум) производителя находится в точке касания изокванты и изокосты(Рис. 8). Это связано с тем, что стремление фирмы к эффективному производству побуждает ее к достижению максимально возможной выработки при заданных затратах на ресурсы, или, что то же самое, к минимзации издержек при производстве заданного объема выпуска.

Комбинация ресурсов, обеспечивающая минимальный уровень совокупных издержек фирмы, называется равновесной (оптимальной) и лежит в точке касания линий изокосты и изокванты, как это представлено на рисунке 8.

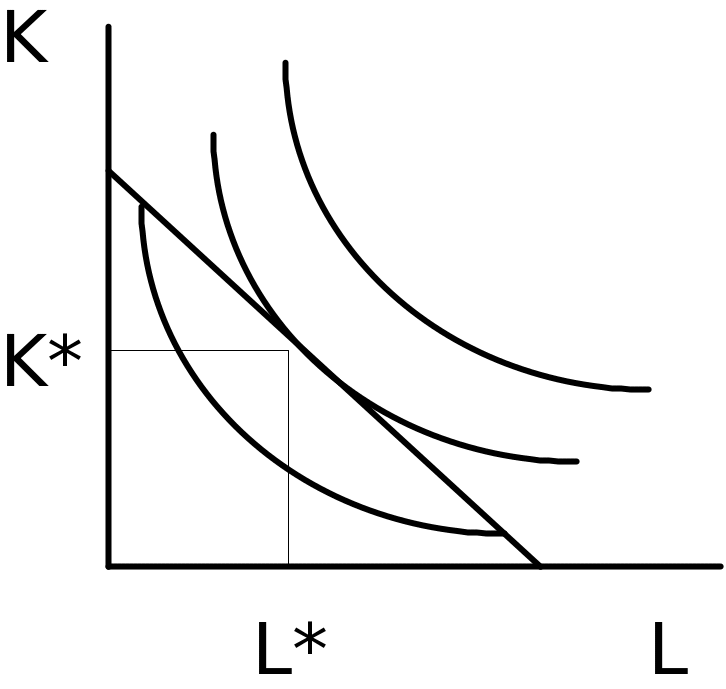
Рис.8 Точка оптимума

Оптимальная комбинация ресурсов предполагает выполнение следующих условий:

1) равновесная комбинация ресурсов (K*,L*) всегда лежит на линии изокосты, а не под нею. Это означает, что для минимизации издержек фирма должна полностью использовать средства, предназначенные для покупки ресурсов.

2) в точке равновесия угол наклона кривой изокванты равен углу наклона линии изокосты.

Поскольку tg угла наклона кривой изокванты = ,

tg угла наклона линии изокосты = -PL/PK,

то, следовательно, второе условие оптимума предполагает такое распределение расходов фирмы, при котором предельная норма технологического замещения одного ресурса другим равно отношению их цен.

MRТS=-PL/PK

Экономический смысл данного условия:

MRTS определяет возможность технологического замещения капитала трудом. Отношение цен отражает экономическую способность производителя замещать капитал трудом. Пока эти возможности не сравняются, изменения в соотношении используемых ресурсов будут вести к увеличению объемов выпуска или уменьшению совокупных издержек фирмы.

Второе условие максимизации может быть записано как

или

В случае n количества ресурсов, выражение принимает вид

.

Это означает, что фирма должна распределить свои бюджетные средства так, чтобы получить одинаковый прибавочный продукт на рубль, затраченный на приобретение каждого ресурса.