Выполнение работы.

1. Взвешиваем на технических весах и определяем массу m стержня и М-диска.

2. С помощью штангенциркуля определить диаметр D диска и расстояние l между ребрами призм и центром стержня.

3. Стержень навинчивается на винт подвеса и приводится в состояние колебательного движения (крутильных колебаний). Секундомером измеряют время t₂ количества колебаний n₂=25. Определяется период крутильных колебаний по формуле:

(6),

Опыт повторить три раза.

Затем на винт подвеса навинчивается диск и измеряется его период колебаний T₀ ( как

у стержня - три серии по 25 колебаний). Согласно формулам (4) и (5) получим:

4. Ребро призмы стержня установить в желобок вилки и привести стержень в

колебание. Секундомером измеряется время t₁ некоторого количества n₁ (n₁=25) полных колебаний и находим период колебаний физического маятника:

Опыт повторяют три раза.

Из формулы (2) следует:

5.После вычисления погрешностей, проверить справедливость равенства (1).

Литература:

1. Савельев и.В., Курс общей физики; т.1, § 39 (Момент инерции, стр. 140-144), м, 1982г.

2. Стрелков сп., Механика, § 59, стр. 211-215, м, 1975г. Лабораторная работа № 8 определение момента инерции, теля с помощью крестообразного маятника.

ОБОРУДОВАНИЕ:

I. Крестообразный маятник с перемещающимися грузами.

2. Вертикальный масштаб.

3. Набор грузов по 50 грамм.

4. Штангенциркуль.

5. Секундомер.

Краткая теория.

Моментом инерции материальной точки массой m находящейся на расстоянии r от оси вращения, называется произведение масcы этой точки на квадрат расстояния от оси вращения, т.е.

Если имеем дело с телом, то моментом инерции его называется сумма моментов инерции всех его точек, т.е. ,

Во вращательном движении момент инерции играет ту же роль, какую в. поступательном движении играет масса. Поэтому определение момента инерции имеет большое практическое значение. Определить момент инерции тела относительно какой-нибудь оси можно путем вычисления, если тело имеет правильную форму и известно распределение массы внутри тела. Но чаще всего приходится определять момент инерции тела относительно какой-нибудь оси опытным путем.

В нашей работе для этой цели применяется крестообразный маятник (рис.1). Он представляет собой маховик, с четырьмя взаимно перпендикулярными стержнями, вдоль которых могут перемещаться грузы. Для этих грузов нам и предстоит найти момент инерции.

На общей оси маятника находится валик; на валик намотана нить

с привязанным грузом.

Основное выражение динамики для вращающегося тела выражается так:

(1)

где

М - момент силы, под влиянием которой тело вращается вокруг оси,

I -| момент инерции вращающегося тела,

- угловое ускорение тела.

Из уравнения-(1) имеем:

(2)

Таким образом, для определения инерции вращающегося тела нужно знать момент вращающей силы и угловое ускорение тела. Будем искать эти величины.

Привяжем к нити маятника некоторый груз и представим ему возможность падать. Это падение будет равноускоренным.

Если высота падения h, а время падения t, то

где а-линейное ускорение.

Отсюда:

Но с таким ускорением будут двигаться все тела (точки) на поверхности валика. Измерив радиус валика r, можно найти угловое ускорение Е маховика:

(3)

Вращающим моментом силы называется произведение силы на ее плечо.

Напомним, что, плечом называется расстояние от оси вращения до прямой, совпадающей с направлением действия силы. В нашем примере плечо силы равно радиусу валика.

Найдем, чему равна сила, вращающая маятник.

На груз массы m действуют:

I) сила тяжести Р = mg

2) натяжение нити (силы противоположного направления) P_H

Результирующая сила: F=ma.

По второму закону Ньютона, эта сила, действуя на груз массы m будет перемещать его с ускорением a, т.е.

Отсюда:

Но натяжение нити P_H численно равно, той силе, которая приводит во вращение крестообразный маятник. Поэтому момент этой силы

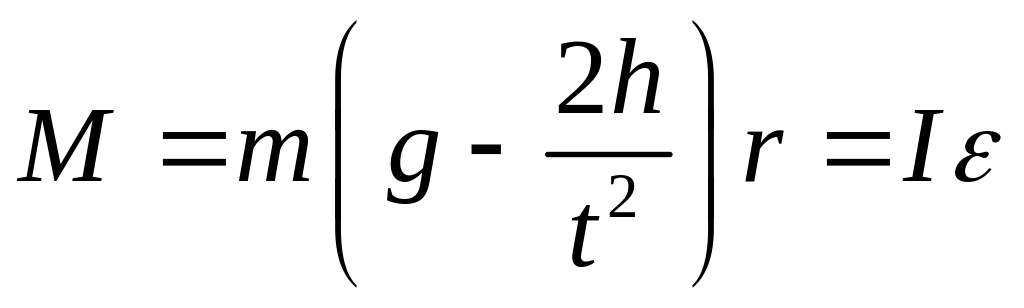; (4)

Подставив значения М и из формул (3) л (4) в формулу (2), получим величину момента инерции вращающегося маятника:

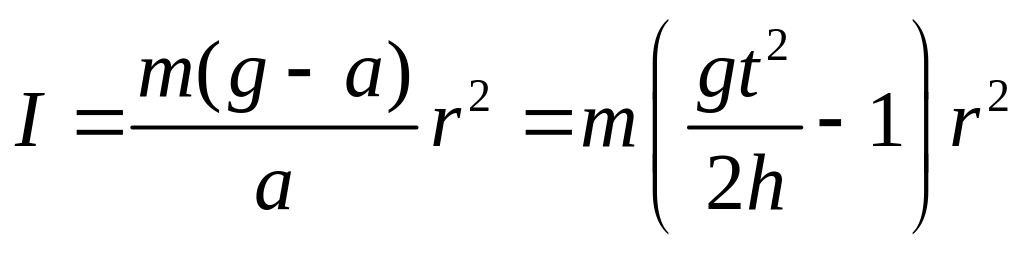(5)