Лещенко В.Г. Изучение усилителя электрических сигналов.

ИЗУЧЕНИЕ СВОЙСТВ УСИЛИТЕЛЯ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ. ОПРЕДЕЛЕНИЕ ЧАСТОТНОЙ И АМПЛИТУДНОЙ ХАРАКТЕРИСТИК.

Цель работы: ознакомление с принципами усиления электри­ческих сигналов и свойствами реальных усилителей; обучение методам регистрации амплитудной и частотной характеристик усилителя и правильному выбору усилителя в соответствии с параметрами усиливаемого сигнала.

Задача регистрации переменных электрических полей, генерируемых живым организмом (биопотенциалов) имеет большое значение для целей диагностики многих заболеваний и определения функционального состояния различных органов. Однако амплитуда этих биопотенциалов чрезвычайно мала (доли и единицы миллиВольт), поэтому они могут быть зарегистрированы только после их предварительного усиления. При этом очень важно провести усиление амплитуды и одновременно сохранить форму этих биопотенциалов.

Усилителем электрических сигналов называют устройство, увеличивающее интенсивность подаваемого сигнала за счет энергии постороннего источника. Поступление энергии источника к потребителю регулируется управляющим элементом усилителя, в качестве которого используются электронные лампы, транзисторы и микросхемы..

Основной характеристикой усилителя является коэффициент усиления К, равный отношению амплитуды сигнала (напряжения, тока или мощности) на выходе усилителя к соответствующей амплитуде сигнала на его входе:

; ; (1)

В зависимости от того, какой из параметров сигнала подлежит усилению, различают усилители напряжения, тока и мощности.

Основным требованием, предъявляемым к усилителю биопотенциалов, является увеличение амплитуды сигнала без искажения его формы.

Рассмотрим этот вопрос подробнее. Биопотенциалы (t), генерируемые живым организ­мом, носят обычно периодический характер, то есть повторяются с некоторой частотой , где Т–пери­од повторения.

Такой периодический потенциал согласно теореме Фурье мо­жет быть представлен в виде суммы гармонически изменяющихся потенциалов, частоты которых кратны основной частоте v₀ или основной циклической частоте ω₀=2πv₀ повторения биопо­тенциала:

(t) = а₀ + а₁ cos(ω₀t + ₁) + а₂ cos(2ω₀t + ₂) + …+ а_n cos(nω₀t + _n) (2)

или в краткой записи:

(t) = а₀ + а_m cos(mω₀t + _m). (2а)

Здесь а₀ – постоянная составляющая сигнала (во многих случаях она равна нулю), а_m cos(mω₀t + _m)) – его гармонические поставляющие, имеющие амплитуду а_т, циклическую частоту (mω₀) и началь­ную фазу _m. Первая из этих составляющих (при m = 1) описывает колебание, происходящее с основной частотой v₀ и называ­ется основным тоном сигнала, а остальные составляющие (при m = 2, 3, 4...) называются обертонами, или соответственно 2-ой, 3-ей, 4-ой и т.д. гармониками сигнала. Число n таких гармонических составляющих определяется видом (сложностью) функции (t) и может достигать нескольких сотен.

О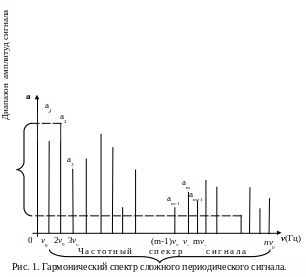 бласть частот, занимаемая основным тоном и оберто­нами сигнала (то есть область от v₀ до v_n = nv₀) называется частотным спектром сигнала, который в совокупности с соответствующими амплитудами а₀, а₁, а₂, … , а_n определяет гармо­нический спектр рассматриваемого сигнала (рис.1).

При прохождении сложного сигнала (2) через усилитель каждая из его гармонических составляющих увеличивается по амп­литуде в какое-то число раз К_m, равному коэффициенту усиления на частоте этой гармоники и в общем случае различному для разных гармоник. В процессе усиления могут изменяться и начальные фазы гармоник _m. На выходе усилителя происходит суммирование этих усиленных гармонических колебаний, в результате чего выходной сигнал будет представлять собой некую периодичес­кую функцию Е(t):

Е(t) = К₀а₀+ К_mа_m cos (mω₀+ Ф_m), (3)

которая может существенно отличаться по форме от входного сигнала (t).

Из сопоставления выражений (2а) и (3) видно, что форма периодического сигнала (t) на выходе усилителя будет соответствовать форме сигнала (t) на его входе только в том случае, если коэффициенты усиления разных гармоник К_m будут одинаковы на всех частотах, имеющихся в спектре сигнала, то есть если К₀ = К₁ = K₂ = … = K_n =const = K, и кроме того, еcли начальные фазы гармоник при усилении не изменятcя: Ф_т =  _m.. Действительно, только при выполнении этих условий все коэффициен­ты K_m можно вынести из под знака суммы и мы на выходе усилителя получим усиленный в К раз входной сигнал:

Е(t) = K a₀ + a_m cos (2mv₀+ _m) = К· (t), (3а)

Таким образом, только в тех случаях, когда коэффициент усиления не зависит ни от частоты, ни от амплитуды сигнала, а начальные фазы гармоник не изменяются в процессе усиления, на выходе усилителя получается переменный сигнал, повторяющий по форме сигнал на его входе, но усиленный в К раз. Только при этих условиях возможно усиление сигнала без искажения его формы. Усилитель, всегда удовлетворяющий этим условиям можно назвать идеальным усилителем.

Однако в действительности, у любого реального уси­лителя коэффициент усиления всегда зависит и от частоты и от амплитуды входного сигнала, то есть К = K(, a_m), что приводит соответственно к частотным и амплитудным искажениям усиливаемого сигнала.

Не сохранение фазы усиливаемых гармонических составляющих сигнала ведёт к фазовым искажениям сигнала.

Итак, реальный усилитель может существенно искажать форму усиливаемых сигналов, что не допустимо в медицине, т.к. именно форма этих сигналов (напр. ЭКГ) часто имеет определяющее диагностическое значение.

Поэтому важно выяснить, при каких условиях реальный усилитель не будет искажать усиливаемый сигнал. Для этого необходимо знать, как именно зависит коэффициент усиления реального усилителя от частоты и амплиту­ды входного сигнала.

1. Частотная характеристика усилителя – это зависимость коэффициента его усиления от частоты к(V).

Примерная частотная характеристика усилителя показана на рис. 2.

У идеального усилителя коэффициент усиления не зависит от частоты: К () = const и его частотная характеристика представляет собой прямую, параллельную оси абсцисс. У реального усилителя коэффициент усиления лишь примерно постоянен в неко­тором диапазоне частот, а вне его быстро спадает (рис.2). Это непостоянство коэффициента усиления ведёт к частотным искажениям сигнала, однако экспериментально установлено, что они малы и ими можно пренебречь, если изменения коэффициента усиления не превышают 30% от его максимального значения.

В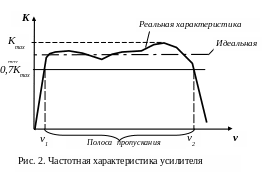 связи с этим область частот от ₁ до ₂, в преде­лах которой значения коэффициента усиления лежат в интервале от K_max до 0,7 K_max принято называть полосой пропускания усилителя.

Если частотный спектр усиливаемого сигнала полностью попадает в полосу пропускания, то частотные искажениями сигна­ла не превосходят до­пустимых норм и на влияют на диагностические свойства кривых.

Если же спектр усиливаемого сигнала хотя бы частично выходит за пределы полосы пропускания усилителя, то частотные искажения будут велики, и такой усилитель не пригоден для усиления этого сигнала.

2. Амплитудная характеристика усилителя представляет собой зависимость амплитуды сигнала (напряжения, тока или мощности) на выходе усилителя от амплитуды сигнала на его входе и является второй важнейшей характеристикой реального усилителя.

Д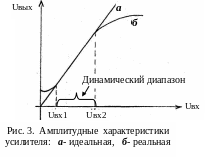 ля идеального усилителя эта зависимость всегда линейны, так как его коэффициент усиления К постоянен: U_вых= К·U_вх. Поэтому амплитудная характеристика идеального усилителя представляет прямую линию, идущую из начала координат (прямая «а» на рис.3), тангенс угла наклона которой к оси абсцисс равен коэффициенту усиления:

Кривая б на рис.3 соответствует типичной амплитудной характеристике реального усилителя. Она линейна лишь в определённом диапазоне входных напряжений, а именно при U_вх1 U_вх U_вх2 .

Только в пределах этого диапазона коэффициент усиления постоянен, амплитудные искажения сигнала отсутствуют и усилитель подобен идеальному.

Этот диапазон входных напряжений от U_вх1 до U_вх2, в пределах которого отсутствуют нелинейные (амплитудные) искажения, назы­вается динамическим диапазоном усилителя. Его часто выражают в децибелах:

. (4)

Вне этого диапазона амплитудная характеристика становится нелинейной, и если амплитуды гармоник входного сигнала выходят за пределы этого диапазона, то будут наблюдаться амплитудные искажения формы усиливаемого сигнала.

Таким образом, чтобы правильно (без искажений) произвести усиление исследуемого сигнала реальным усилителем, необходимо выполнить два условия:

1. Частотный спектр усиливаемого сигнала должен полностью попа­дать в полосу пропускания усилителя.

2. Диапазон амплитуд усиливаемого сигнала должен находиться в пределах динамического диапазона усилителя.

Дифференциальный усилитель

Биопотенциалы, возникающие в организме человека, очень малы по величине и в десятки и сотни раз меньше посторонних электромагнитных сигналов (помех), самопроизвольно поступающих на вход усилителя. В результате этого на выходе обычного усилителя буде наблюдаться очень большой и беспорядочно изменяющийся сигнал помехи, на фоне которого практически невозможно наблюдать слабый исследуемый сигнал. Поэтому, для усиления биопотенциалов используются дифференциальные усилители. Их преиму­щество состоит в том, что они усиливают полезный сигнал и уничтожают сигнал помехи, то есть дифференциальный усилитель обладает высокой помехозащищённостью. Рассмотрим прин­цип его действия этого усили­теля (ОУ).

Особенностью дифференциального уси­лителя является наличие у него двух входов – инвертирующего (Вх1) и неинвертирующего (Вх2) и од­ного общего выхода. Коэффициен­ты усиления для этих входов одинаковы по величине, но противоположны по знаку: U_вых1= – К U_вх1 ; U_вых2= + К U_вх2

Напряжение на инвертирующий вход (–) поступает между общей точкой ₀ и Вх 1, а на неинвертирующий (+) – между общей точкой и Вх 2 (см. Рис.4).

Если на первый вход подать напряжение U_bx1, и на второй – напряжение U_bx2, то на выходе усилителя будет усиленная разность этих сигналов:

U_вых = U_вых2+U_вых1 = К (U_вх2 – U_вх1) .

Поэтому такой уси­литель и называют дифференциальным, так как он усиливает не са­ми сигналы, а их разность (англ. difference – разность).

Если на оба входа дифференциального усилителя поступают одинаковые сигналы (и по амплитуде и по фазе), то на выходе усилителя будет ноль, так как оба сигнала на выходе уничтожат друг друга.

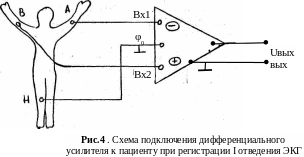
Именно это свойство дифференциального усилителя оказывается чрезвычайно полезным для борьбы с помехой при регистрации слабых сигналов. Предположим, что необходимо усилить разность потенциалов в I-ом отведении ЭКГ. На рис.4 показано, что электроды А(левая рука) и В (правая рука) подключены к клеммам Вх1 и Вх2 усилителя соответственно.

Третий электрод соединяет общую клемму усилителя φ₀ с правой ногой пациента, не участвующей отведениях Эйнтховена, и служит опорным.

Напряжение, возникающее между электродом А (левая рука) и опорным электродом (правая нога) подаётся на вход 1 усилителя, а напряжение между электродом В (правая рука) и опорным электродом подаётся на вход 2, при этом на оба входа одновременно поступают идентичные помехи U_пом, напряжения которых могут быть значи­тельно больше напряжения полезного сигнала:

U_вх1 = φ_А–φ₀ +U_пом ; U_вх2 = φ_В–φ₀ +U_пом ;

На выходе усилителя получим усиленную в К раз разность этих входных сигналов: U_вых = К (U_вх2 – U_вх1) = К(φ_В–φ_А) , которая представляет собой усиленное в К раз I отведение ЭКГ, а сигналы помехи взаимно уничтожаются.

Отметим, что потенциал φ₀ опорного электрода тоже уничтожается и не влияет на конечный результат, поэтому этот электрод можно накладывать на любую точку тела пациента, но подключать опорный электрод к пациенту надо обязательно, чтобы правильно подвести напряжения к обоим входам дифференциального усилителя. Из соображений удобства договорились накладывать его на правую ногу пациента, свободную от подключения стандартных отведений.