
Высоцкая Мария Николаевна
группа 10-ПГС-3
вариант №70
Задача С-8
Расчёт фермы
Условие:
Плоская ферма нагружена тремя силами, приложенными в трёх узлах. Порядковые номера сил и нагруженных узлов совпадают. Действующие силы заданы их проекциями на оси X и Y правой системы координат.
Выполнить расчёт фермы:
Определить реакции опор, выполнить проверку;
Определить усилия в стержнях фермы методом вырезания узлов и выполнить графическую проверку;
Определить усилия в стержнях 2, 3, 4 методом сквозных сечений.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Определение опорных реакций
Составим уравнения равновесия сил, приложенных к ферме. Связи заменим реакциями. В точке А – неподвижная шарнирная опора – реакции по оси Ох и оси Оу. В точке В – подвижная шарнирная опора – реакции по оси Оу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
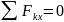 ;
;
 ;
;
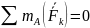






Проверка:
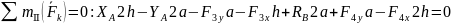

Реакции найдены верно:

Определение сил в стержнях фермы способом вырезания углов.
Вырезаем
последовательно узлы фермы и составляем
уравнения равновесия
 ;
;
 .
Начинаем с узла, где меньше всего усилий.
.
Начинаем с узла, где меньше всего усилий.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Узел а:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 sinα=
sinα=


Найти:

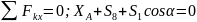
 (сжат)
(сжат)

 (сжат)
(сжат)
Узел ⅰ:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 sinα=
sinα=

Найти:


 (сжат)
(сжат)


Узел ⅳ:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 sinα=
sinα=

 кН
кН


Найти:


 (растянут)
(растянут)
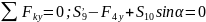
 (растянут)
(растянут)
Узел ⅴ:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


Найти:


 (растянут)
(растянут)

Узел ⅱ:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 sinα=
sinα=
 cosβ=
cosβ=
 sinβ=
sinβ=



Найти:
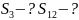

 /cosβ=
/cosβ=
=( )/
=(
)/
=( )/
)/



 кН
(растянут)
кН
(растянут)
 кН (сжат)
кН (сжат)
