МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

СЕВМАШВТУЗ

ФАКУЛЬТЕТ : IV

КАФЕДРА : ФИЗИКИ

Лабораторная работа

ИЗУЧЕНИЕ СВОЙСТВ ГАЗОВ

СЕВЕРОДВИНСК

2002

ЛАБОРАТОРНАЯ РАБОТА №14

ИЗУЧЕНИЕ СВОЙСТВ ГАЗОВ.

1. ЦЕЛЬ И МЕТОД РАБОТЫ

Определение коэффициента внутреннего трения воздуха. Метод основан на использовании формул Пуазейля.

2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Понятие внутреннего трения (вязкости).

Явлением внутреннего трения (вязкости) называется появление сил трения между слоями газа (или жидкости), движущимися друг относительно друга параллельно и с разными по величине скоростями. Слой, движущийся быстрее, действует с ускоряющей силой на более медленно движущийся слой. Наоборот, медленно движущийся слой тормозит более быстро движущийся слой газа. Силы внутреннего трения, которые возникают при этом, направлены по касательной к поверхности соприкосновения слоев. Причиной вязкости является наложение упорядоченного движения слоев газа с различными скоростями и теплового хаотического движения молекул со скоростями , зависящими от температуры.

ОПРЕДЕЛЕНИЕ:

С ила вязкости , которую нужно преодолеть для того, чтобы два смежных слоя газа скользили один по другому, пропорциональна площади S слоев и градиенту скорости , то есть

(1)

З

десь градиент скорости представляет собой изменение скорости на единицу длины, взятой перпендикулярно к слоям (рис.1) (иными словами - изменение скорости движения вдоль координаты ).

Рис. 1

- коэффициент внутреннего трения газа.

- нормаль к границе соприкасающихся слоев газа;

f – сила, действующая на площадь слоя газа при градиенте скорости .

(2)

ОПРЕДЕЛЕНИЕ:

Коэффициент внутреннего трения газа равен силе, действующей на единицу площади слоя, когда на единице длины, взятой перпендикулярно к слоям, скорость меняется на единицу ( ).

За единицу измерения коэффициента внутреннего трения (иди вязкости) в системе СИ принимается Ньютон-секунда на квадратный метр ( ).

ОПРЕДЕЛЕНИЕ:

Ньютон-секунда на квадратный метр - это коэффициент динамической вязкости (внутреннего трения) такого газа, в котором 1м² слоя испытывает силу трения 1Н при градиенте скорости .

Е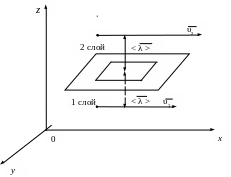 сли (согласно рис.1), то молекулы перейдя из слоя с меньшей скоростью в слой с большей скоростью, ускоряют свое движение, но замедляется движение молекул в слое. При этом происходит перенос импульсов упорядоченного движения молекул.

Покажем получение формулы (1), для чего мысленно выделим в газе площадку , параллельную слоям, текущий с различными скоростями и , так что .

Рис.2

Считаем температуру Т и давление Р газа постоянными, тогда концентрация и средняя скорость теплового движения молекул газа будут одинаковыми во всем объеме.

Ввиду полной беспорядочности теплового движения молекул газа, ни одно из направлений теплового движения не имеет преимущества перед другими, поэтому можно считать, что 1/3 всех молекул движется вдоль оси ОZ, 1/3 - вдоль оси ОХ и 1/3 - вдоль оси ОУ. Из них половина будет двигаться в положительном направлении осей, половина - в противоположном, т.е. 1/3 всех молекул будет двигаться вдоль каждого из выбранного направления осей.

Пусть слой 1 лежит под площадкой на расстоянии средней длины свободного пробега молекул , а слой 2 - над площадкой на том же расстоянии . Тогда молекулы, летящие со средней скоростью теплового движения из слоя 1 и из слоя 2 по направлению к площадке , достигнут ее без столкновения. Число молекул , проникающее через площадку снизу из слоя 1 за время будет равно:

(3)

Эти молекул перенесут через площадку импульс , равный

(4)

Аналогично из слоя 2 через площадку за время будет перенесен импульс , равный

В результате через площадку будет перенесен импульс, равный

(5)

Разность скоростей представляет собой приращение скорости на расстоянии . Следовательно, можно записать, что , откуда и, следовательно,

(6)

Так как есть плотность газа , то получим

.

А так как , то сила внутреннего трения F , действующая на площади соприкосновения слоев , будет равна

(7)

Так как , , в данном случае постоянные, то введя обоз­начение

, (8)

получим окончательное выражение для силы трения:

(9)

ОПРЕДЕЛЕНИЕ:

Закон Пуазейля показывает, что средняя скорость ламинарного течения газа (или жидкости) по трубе пропорциональна падению давления на единицу длины трубы, квадрату радиуса трубы и обратно пропорциональна коэффициенту внутреннего трения газа (или жидкости)

(10)

Объем газа , протекающий в 1 сек. через поперечное сечение трубы S, равен произведению средней скорости течения на площадь поперечного сечения, т.е. и при

(11)

За любой промежуток времени объем протекающего газа определяется формулой Пуазейля

(12)

Формула (11) или (12) дает возможность определить коэффициент внутреннего трения газа. Внутреннее трение в газе или жидкости - это одно из явлений переноса. Поэтому характер течения газа или жидкости можно судить по значению числа Рейнольдса:

(13)

где - средняя скорость течения.

При - течение ламинарное, при - турбулентное.

Формула (13) записана при соблюдении следующих условий:

- малые перепады давления на концах трубы.

- ламинарное течение газа (или жидкости)

- постоянная температура.

Внутреннее трение в газе (жидкости) предполагает взаимодействие молекул путем столкновений, для которого характерны следую­щие понятия:

- средняя длина свободного пробега молекул как среднее расстояние, которое молекула проходит без столкновения.,

- эффективный диаметр молекул ( ) как минимальное расстояние, на которое сближаются при столкновении центры двух молекул. При этом считается, что молекулы ведут себя как упругие шары, между которыми действуют силы взаимного отталкивания,

• эффективное сечение столкновения молекул как

3.Описание экспериментальной установки, теория метода и постановка задачи.

на рис.3 представлена схема установки

Рис.3

В нее входит : 1 - капилляр известной длина и радиуса ;

2 – манометр, в котором в качестве рабочего тела используется жидкость с известной плотностью _1;

3 - делительная воронка с делениями ;

4 – мензурка;

5 - влагопоглотитель ;

6 - секундомер для измерения времени вытекания жидкости из делительной воронки.

В данной работе для определения коэффициента внутреннего трения газа используем формулу Пуазейля (12) (сжимаемостью газа можно пренебречь). Если перепад давлений измерять с помощью жидкостного манометра, то .

Здесь: - плотность, жидкости в манометре.

- разность высот уровней жидкости в манометре.

Из формулы (12) для запишем:

(14)

где V(м³)–объём жидкости, вытекающей из делительной воронки за время t₀.

Обозначим: , тогда формула (14) примет вид:

(15)

По этой формуле, измерив , , , и , зная , можно определить .

Дополнительно можно определить другие важнейшие характеристики газа (2), в частности, среднюю длину свободного пробега молекул по формуле

, (16)

эффективный диаметр молекул по формуле

(17)

здесь R - газовая постоянная (табл.),

- постоянная Больцмана (табл.),

- молярная масса воздуха (табл.),

, - давление и температура воздуха во время проведения опыта (см. приборы),

₁-коэффициент внутреннего трения (из опыта).

4.Порядок проведения работы.

1. Перед началом работы проверить, чтобы влагопоглотитель был открыт, уровни жидкости в манометре были на одной высоте делительная воронка была заполнена водой на 2/3 объема, мензурка была пустой, секундомер исправным.

2. Открыть кран делительной воронки, подождать, пока течение воздуха в капилляре установится, т.е. уровень жидкости в манометре перестанет изменяться. Зафиксировать разность уровней манометра.

3. Подставить вместо стакана под струю мензурку, и включив секундомер, измерить объем жидкости, вытекшей из делительной воронки (соответственно объем газа, продавленного через капилляр) в течение 40-50 секунд.

Внимание! Объём вытекающей воды не должен превышать 20 мл.

4. Закрыть кран делительной воронки.

5.Данные эксперимента занести в таблицу:

№ п/п
1
2
3
4
5

6. Опыт повторить пять раз при разной скорости вытекания воды из делительной воронки (разных ), регулируя ее краном делительной воронки, и результаты занести в таблицу.