МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

СЕВМАШВТУЗ

ФАКУЛЬТЕТ: IV

КАФЕДРА: ФИЗИКИ

Лабораторная работа

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА

СЕВЕРОДВИНСК

2001

Лабораторная работа № 4 определение момента инерции твердого тела

1. Цель и метод работы.

Научиться определять момент инерции твердого тела динамическим методом, в основе которого лежат законы о сохранении и превращении энергии.

2. Основные теоретические положения.

Пусть твердое тело А имеет ось вращения . Если к телу А будет приложена некоторая сила F, не проходящая через ось вращения и не параллельная этой оси, то тело А будет вращаться относительно оси .

Р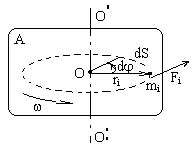 азобьем тело А на элементарные точки с массами m_ , и пусть на эти точки действуют силы F_ , лежащие в плоскости, перпендикулярной оси . Под действием силы F_точке m_ будет сообщено ускорение , т. е.

(1)

Рис.1 Если точка m_ находится от оси на расстоянии , то , где - угловое ускорение точки m_ относительно . Тогда

(2)

О пыт показал, что есть функция от и , то есть , тогда, умножив обе части уравнения (2) на , получим:

_т. е.

_, (3)

г де называется моментом силы, который является мерой взаимодействия при вращательном движении. Тогда по аналогии со вторым законом Ньютона для поступательного движения поставим в аналогию  ,  и  , тогда отсюда видно, что для материальной точки m_ при движении ее вокруг оси по окружности радиусом _ величина является мерой инертности и называется моментом инерции материальной точки относительно оси при вращательном движении и обозначается .

Т огда для твердого тела А мера взаимодействия тела с внешними механическими силами, вызывающее вращение его относительно оси будет равно

(4)

Но так как является одинаковым для всех материальных точек тела,

т.е. , то

т.е. (5)

Уравнение (5) является основным законом динамики для тел, вращающихся вокруг неподвижной оси, или Вторым Законом Ньютона для вращательного движения твердого тела,

где – результирующий момент силы, действующей на тело А относительно оси О, О,’ ;

J_А – момент инерции тела (мера инерции тела).

Так как то уравнение (5) примет вид:

или

или

, (6)

где - момент импульса тела (момент количества движения).

Момент инерции тела, вычисленный относительно оси, проходящей через центр тяжести, называется центральным моментом инерции J_c .

Для любой другой оси, параллельной центральной оси (проходящей через центр тяжести тела), момент инерции выражается формулой Гюйгенса-Штейнера:

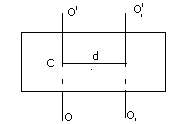
, (7)

где m - масса тела; d - расстояние между осями (рис.2). При вращении твердого тела под действием некоторого момента сил M_A 0, над каждой элементарной точкой m_совершаетсяработа на перемещение:

Рис. 2

т.е. , (8)

а полная работа, затраченная на движение материальной точки при вращении твердого тела :

, (9)

то полная работа на вращение тела:

.

Но так как механическая работа А равна изменению энергии T, т.е.

то ; (10)

Тогда под будет пониматься кинетическая энергия твердого тела при вращении.

Если тело одновременно участвует в двух движениях: поступательном со скоростью  и вращательным вокруг оси, проходящей через центр массы, то полная кинетическая энергия тела равна:

(11)