Литература

1. Мышев А.В. Основы прикладной теории кодирования

информации. Учеб. пособие по курсу «Теории кодирования информации». – Обнинск, ИАТЭ, 1999, - 77с.

2. Мышев А.В. Модели активной памяти в технологиях

виртуализации каналов хранения и передачи информации // Программные системы и продукты, 2010, №1, - с.54-59.

3. Морелос - Сарагоса Р. Искусство помехоустойчивого

кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005г., - 320 с.

4. Электронные копии лекций, методичек и др. на накопи-

телях сервера кафедры.

Приложение 1

Кодирование для исправления ошибок: основные положения

Все коды, исправляющие ошибки, основаны на одной общей идее: для исправления ошибок, которые могут возникнуть в процессе передачи или хранения информации, к ней добавляется некоторая избыточность. По основной схеме, используемой на практике, избыточные символы дописываются за информационными, образуя кодовую последовательность или кодовое слово (codeword). На рисунке №1 показана геометрическая иллюстрация процедуры формирования блокового кода (bloch code). Такое кодирование называют систематическим (systematic).

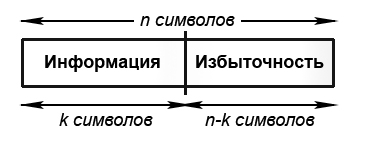
Рис.1. Систематическое блоковое кодирование для исправления ошибок

Это означает, что информационные символы всегда появляются на первых k позициях кодового слова. Символы на оставшихся (n - k) позициях являются различными функциями от информационных символов, обеспечивающими тем самым избыточность, необходимую для обнаружения или исправления ошибок. Множество всех кодовых последовательностей называют кодом, исправляющим ошибки (error correcting code).

Приложение 2.

Корректирующая способность кода и его связь с кодовым расстоянием

Двоичный код С, представляющий собой множество 2ⁿ символьных последовательностей длины n исправляющий ошибки, если передает по информационному каналу не все возможные векторы, может обладать свойством помехоустойчивости. Код С является подмножеством n - мерного двоичного пространства R₂ = {0,1}ⁿ таких, что его элементы максимально удалены друг от друга. В информационном пространстве V₂ расстояние определяется как число позиций, в которых два вектора не совпадают. Пусть ₁ = (х_1,0;х_1,1…_;х_1,n-1) и ₂ = (х_2,0,х_2,1,…,х_2,n-1) два вектора в V₂, тогда хеммингово расстояние между векторами ₁ и ₂ , которое обозначим, как d_x(x₁,x₂), равно

d_x(x₁,x₂) = |{i:х₁, i≠x_2,i, 0≤i≤n}|, (1.1)

где через |A| обычно обозначают число элементов в множестве А.

Для кода С минимальное хеммингово расстояние d_min определяется, как минимум хеммингова расстояния по всем возможным парам различных кодовых слов:

d_min = min {d_x (V₁, V₂)| V₁ ≠ V₂ }. (1.2)

V₁, V₂ C

Пример. Простейшим примером является код повторения длины 3. Каждый информационный бит повторяется три раза. Таким образом, сообщение «0» кодируется вектором V₁ =(000), а сообщение «1» - вектором V₂ = (111). Так как два вектора различаются в трех позициях, то d_x (V₁,V₂) =3. На рисунке №1 показано графическое представление этого кода. Трехмерное двоичное пространство соответствует 2³=8 вершинам трехмерного единичного куба. Хеммингово расстояние между кодовыми словами V₁ = (000) и V₂ = (111) равно числу вершин, через которые проходит соединяющий их путь. Это эквивалентно числу координат, которые необходимо изменить, чтобы преобразовать V₁ в V₂ и наоборот. Таким образом, d_min = 3.

Двоичное векторное пространство V₂ обычно называют хемминговым пространством. Пусть V - кодовое слово кода с Хемминговой сферой S_t(V) радиуса t с центром в точке V является множество векторов (точек) в V₂ на расстоянии, меньшем или равном t от центра V.

S_t(V) ={x C| d_x(x,V) ≤ t}. (1.3)

Следует заметить, что число слов в S_t(V) равно:

|S_t(V)| = , (1.4)

где = Cⁿ_i = . (1.5)

Корректирующей способностью (error correcting capability) t кода С называют наибольший радиус хемминговой сферы S_t(V) для всех кодовых слов V_t ∊ C такой, что для любых различных пар V_i , V_j ∊ C соответствующие им хемминговы сферы не пересекаются, т.е.

t = max {l| S_l(V_i) S_l(V_j) = 0, V_i ≠ V_j } (1.6)

V_i, V_j l

Это соответствует более распространенному определению

t = [(d_min - 1)/2], (1.7)

где через [Х] обозначается целая часть Х, т.е. целое число меньше или равное х.

Отметим, что для определения минимального кодового расстояния произвольного кода С в соответствии с выражением (1.3) необходимо вычислить все 2^k(2^k-1) расстояний между различными парами кодовых слов. Это практически трудноразрешимая процедура даже для сравнительно коротких кодов.

Приложение 3

Порождающая и проверочная матрицы

Если С - двоичный линейный (n, k, d_min) код, который образует k - мерное подпространство, имеющее базис (V₀,V₁,…,V_k-1) такой, что любое кодовое слово V C может быть выражено через базис:

V = U₀V₀ + U₁V₁ +…+ U_k-1V_k-1, (1.8)

где Ui {0,1}, 0 ≤ i ≤ k

Уравнение (1.8) может быть записано через породающую матрицу G и векторное сообщение U=(U₀,U₁,…,U_k-1)

V=UG , (1.9)

где G = = 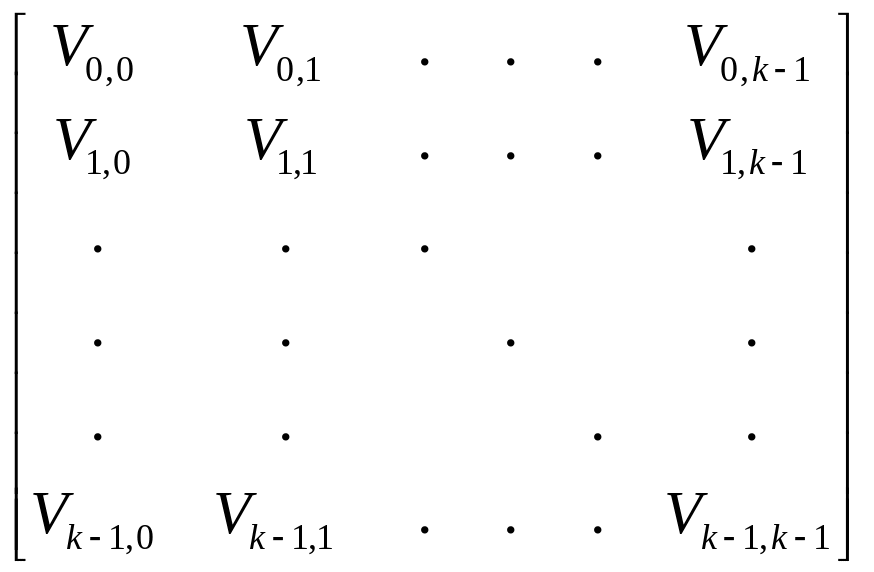(1.10)

Так как G является k - мерным векторным пространством в V₂ , то существует - мерное дуальное пространство (dual space) С┴, которое порождается строками матрицы Н, называемой проверочной матрицей (parity chech matrix), такой что GH^T =0, где через H^T обозначается транспонированная матрица Н. Следует заметить, что любое кодовое слово V C удовлетворяет условию

VH^T =0. (1.11)

Уравнение (1.11) является фундаментальным для декодирования линейных кодов.

Линейный код С┴, который генерируется матрицей Н, является линейным (n, n-h, d┴_min) кодом, который называется дуальным коду С.