8. Моменты распределения, характеристики закона распределения

1. Для дискретной случайной величины:

Математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.

Пусть случайная величина X может принимать только значения x₁, x₂,…, x_n, вероятности которых соответственно равны p₁, p₂,…, p_n. Тогда математическое ожидание M(X) случайной величины X определяется равенством

М(Х) = x₁p₁ + x₂p₂ + … + x_np_n.

Если дискретная случайная величина X принимает счетное множество значений, то

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Дисперсия.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

D(X) = M [X – M(X)]²

Среднее квадратическое отклонение.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называют квадратичный корень из дисперсии.

2. Для непрерывной случайной величины:

Математическое ожидание.

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называют определенный интеграл

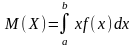
Дисперсия непрерывной случайной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если значения Х принадлежат отрезку [a, b], то

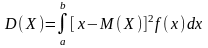
Если возможные значения принадлежат всей оси х, то

.

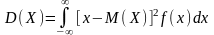Среднее квадратическое отклонение.

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

Список литературы:

Вентцель Е.С.

Теория вероятностей: Учеб. для вузов.-5-е изд. стер.-М.: Высш. шк., 1998.-567 с.: ил.

Содержание.

9. События и их виды…………………………………………………………3

10. Вероятность и ее свойства…………………………………………………3

11. Теорема об умножении вероятностей…………………………………….4

12. Теорема о сложении вероятности совместных и несовместных

событий……………………………………………………………………..7

13. Формула полной вероятности, формула гипотез………………………...9

14. Случайные величины. Закон распределения непрерывной и

дискретной случайной величины………………………………………..10

15. Моменты распределения, характеристика закона распределения ……12

16. Литература………………………………………………………………...13

События и их виды.

Событие – любой возможный исход рассматриваемой ситуации.

События бывают:

1. Достоверными. Событие называется достоверным, если оно обязательно наступает в результате опыта. Например, выпадение не более 6 очков при бросании одной игральной кости.

2. Невозможными. Событие называется невозможным, если оно никогда не произойдет. Например, выпадение 12 очков при бросании одной игральной кости.

3. Несовместными. Два событие называются несовместными, если появление одного из них исключает появление другого в одном и том же опыте. Например, попадание и промах при одном выстреле. События называются попарно несовместными, если несовместны любые два из них.

4. Равновозможными. Событие называются равновозможными, если ни одно из них объективно не является более возможным, чем другие. Например, появление 1,3,4,5 очков при бросании игральной кости.

5. Случайными. Случайным событием называется такой исход наблюдения или эксперимента, который при реализации данного комплекса условий может произойти, а может и не произойти, т.е. это качественный результат эксперимента или экспериментов, если они повторяются многократно. Например, при бросании монеты выпал герб.

6. Противоположными. А – событие, противоположное событию А, происходит тогда, когда не происходит событие А. Например, С₁ – появление новой кометы в текущем году, С₂ – не появление новой кометы в текущем году.

7. Совместными. События называются совместными, если наступление одного из них не препятствует наступлению других.

Набор из нескольких событий называется группой событий.

События образуют полную группу, если они попарно несовместны и в результате опыта осуществляется одно из них. Например, попадание и промах при одном выстреле.