1. Закон распределения дискретной случайной величины

Для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности.

X x₁ x₂ … x_n

p p₁ p₂ … p_n

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X=x₁, X=x₂,…, X=x_n образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

p₁+p₂+…+p_n=1

Если множество возможных значений X бесконечно, то ряд p₁+p₂+… сходится и его сумма равна единице.

• Биномиальное распределение.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появится. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1-p).

Необходимо найти закон распределения дискретной случайной величины X, т. е. числа появлений события А в испытаниях.

Формула Бернулли (*) является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона:

• Распределение Пуассона.

Р_n(k) = λ^ke^-λ/k!

Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (p мало) событий.

• Геометрическое распределение.

Р(Х = k) = q^k-1p

Полагая k = 1,2, … в формуле, получим геометрическую прогрессию с первым членом p и знаменателем q (0 < q < 1):

p, qp, q²p, … , q^k-1p, …

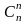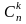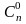(p + q)ⁿ = pⁿ + _np^n-1q + … + p^kq^n-k + … + qⁿ

• Гипергеометрическое распределение.

Р(Х = m) = /

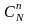
Формула определяет распределение вероятностей, которое называют гипергеометрическим.

2. Закон распределения непрерывной случайной величины

Пусть x – действительное число. Вероятность события, состоящего в том, что X (случайная величина) примет значение, меньшее x, т. е. вероятность события X<x, обозначим через F(x).

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x, т. е.

F(x) = P(X<x).

Иногда вместо термина «функция распределения» используют термин «интегральная функция».

Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности.

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения:

f(x) = F^/(x).