• Биноминальное распределение

Биноминальным называют распределение вероятностей, определяемое формулой Бернулли:

Закон назван биноминальным потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона:

.

Таким образом, первый член разложения pⁿ определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член (np^n-1q) определяет вероятность наступления события n-1 раз;…; последний член qⁿ определяет вероятность того, что событие не появится ни разу.

• Распределение Пуассона

В случаях когда вероятность события мала (n велико, р мало) прибегают к ассимптотической формуле Пуассона:

.

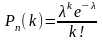Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.

• Геометрическое распределение

Р(Х = k) = q^k-1p

Пологая, что k = 1,2, … в формуле, получим геометрическую прогрессию с первым членом p и знаменателем q (0 < q < 1):

p, qp, q²p, … , q^k-1p, …

По этой причине распределение называют геометрическим.

• Гипергеометрическое распределение

Р(Х = m) = С^m_MC^n-m_N-M/Cⁿ_N.

Формула определяет распределение вероятностей, которое называют гипергеометрическим.

Моменты распределения. Характеристики закона

Распределения.

• Математическое ожидание

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Математическое ожидание М(Х) случайной величины Х определяется равенством:

М(Х) = х₁р₁ + х₂р₂ + … + х_nр_n.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то:

,

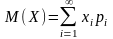причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическое ожидание непрерывной случайной величины X = f(x) определяется следующим образом:

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной:

М(С) = С.

2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = СМ(Х).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X)M(Y).

4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

M(X+Y) = M(X) + M(Y).

• Дисперсия случайной величины

Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[X – M(X)]² = M(X²) – [M(X)]².

Свойства дисперсии:

1. Дисперсия постоянной величины С равна нулю:

D(C) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(CX) = C²D(X).

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D(X+Y) = D(X) + D(Y).

• Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины Х называют корень квадратный из дисперсии:

.

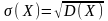Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Х^k:

v_k = M(X^k)

Центральным моментом порядка k случайной величины X называют математическое ожидание величин (X – M(X))^k:

μ_k = M [(X – M(X))^k]

Легко выводятся соотношения, связывающие начальные и центральные моменты:

μ₂=v₂-v₁²

μ₃=v₃-3v₂v₁₊v₁³

μ₄=v₄-4v₃v₁₊6v₂v₁² -3v₁⁴