Случайные величины. Закон распределения непрерывной и дискретной случайной величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Законом распределения случайной величины называется соотношение между возможными значениями случайной величины и соответствующими им вероятностями. Для дискретной случайной величины закон распределения вероятностей представляется в виде ряда распределения. Взаимосвязь может быть задана графически или в виде таблицы
Ряд распределения дискретной случайной величины
xi |
x1 |
x2 |
… |
xn |
Pi |
P1 |
P2 |
… |
Pn |
Для непрерывной случайной величины такую характеристику построить нельзя. Непрерывная случайная величина может иметь бесчисленное множество значений, сплошь заполняющих промежуток. Составить таблицу невозможно. Кроме того, каждое отдельное значение непрерывной случайной величины, как правило, не обладает никакой отличной от нуля вероятностью. Поэтому для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он был описан для дискретной величины, но в то же время различные области возможных значений случайной величины Х не являются одинаково вероятными.
Для количественной характеристики распределения вероятностей непрерывной случайной величины пользуются не вероятностью события X=x, а вероятностью события X<x, где x – некоторая текущая переменная. Вероятность этого события является функцией от x, называется функцией распределения случайной величины X и обозначается F(x); F(x)=P(X<x).
Рассмотрим некоторые наиболее важные законы распределения случайных величин.
Равномерное распределение
Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.
где С = Const. Используя условие нормировки, определим С.
,
откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид:
(14.1)
Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:
(14.2)
Изобразим графики f(x) и F(x):
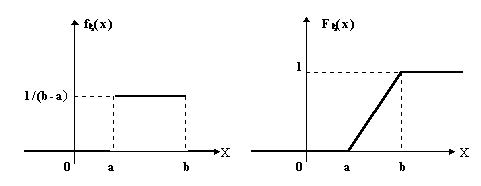
Определим числовые характеристики данной случайной величины:
(14.3)
(14.4)
(14.5)
Наконец, найдем вероятность попадания значений равномерно распределенной случайной величины на интервале (a,b) в интервал (a , b ):
(14.6)
Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности). С такими случайными величинами часто встречаются в измерительной практике при округлении от счетов измерительных приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является случайной величиной x , которая с постоянной плотностью вероятности принимает любое значение между соседними целыми делениями.